某机床伺服电机悬置刚度区间型稳健优化方法研究

王 营，吴进军，钱 蒙，张利强

（机械科学研究总院集团有限公司 中机生产力促进中心，北京 100044）

0 引言

目前，传统的确定性优化方法（即假定变量的优化值可以被无偏差的实现）已经广泛应用于伺服电机和动力总成悬置的刚度、位置等参数的优化[1，2]。但是，在悬置的制造、安装和使用过程中，刚度及位置的实际值与其优化值必然存在一定程度的偏差（称之为不确定性），从而造成悬置系统的固有频率和解耦率等性能指标也与预期的优化值不同。因此，在悬置参数优化阶段准确预测悬置系统固有频率和解耦率的变化特征有重要的理论和工程实际意义。

研究不确定性问题主要有三种方法：概率方法、模糊方法和区间方法[3]。概率方法需要获取不确定参数的概率密度函数等统计信息，模糊方法也需要知道模糊参数的隶属度函数，它们的获取，一般需要通过大量试验或经验，成本较高，精度却不高。区间方法是最近几十年才出现的数学上的一个新兴分支，其优势是只需要不确定参数的上、下界限，因此更容易被应用。

Sirafi和Chang[4]研究了悬置刚度的波动对某悬置系统解耦率的影响。Qatu[5]分析了悬置刚度的变化对悬置系统固有频率的影响。Jiang等[6]把结构载荷、弹性模量或泊松比当作区间参数，提出了一种区间规划方法。吴杰等[7]把悬置刚度看作随机参数和区间参数，对悬置系统进行了优化研究，结果表明二者一致性较好。

文中采用区间数表征设计变量的不确定性，给出区间型稳健优化方法对某机床伺服电机悬置刚度进行稳健优化，其中考虑了刚度设计值的偏差对系统性能指标的影响，并对优化结果进行稳健性分析，验证稳健优化方法的有效性。

1 稳健性优化和分析原理

图1是确定性优化和稳健优化的原理图[7]。确定性优化的解通常位于约束条件的边界，当由于误差而发生波动时，优化方案的实际值可能进入不可行域而使优化失效。因此，确定性优化方法虽然获得了优化方案，却不能确保方案的稳健性。

稳健优化方法不仅要优化目标函数，还要降低目标函数和约束条件对设计变量的灵敏度。优化方案的稳健性可以用约束条件的满足程度和目标函数对设计变量的灵敏度大小来衡量。

图1 确定性优化和稳健优化的原理Fig.1 Principle of deterministic optimization and robust optimization

若设计变量为正态分布随机变量，则优化方案的稳健性可以用目标函数及约束条件的σ水平（σ为标准差）来衡量。每个σ水平对应的正态分布曲线下的面积，正是目标函数值或约束条件值落在其中的概率 （或称为可靠度）[8]。表1中给出了不同σ水平对应的概率（或可靠度）及每百万产品的次品个数（DPM）。

表1 不同水平对应的概率和每百万产品的次品个数Tab.1 Relation between level and probability or DPM

2 悬置系统的区间型稳健优化模型

受到伺服电机布置空间的限制，不对悬置的安装位置和安装角度进行优化，故只优化悬置刚度。因此，确定性优化模型可表示为：

其中，fi—第i个自由度方向的固有频率；di—对应于频率fi的解耦率；wi—权重；fiL和fiU分别为fi的下、上界限，diL为 di的下界；kj—第 j个刚度设计变量，kjL和 kjU分别为kj的下、上界；l为设计变量个数。

考虑到悬置刚度的实际值与优化值之间的偏差，为使悬置系统频率和解耦率的优化值更加稳健，在优化时，应考虑到刚度名义值的波动对优化结果产生的影响。因此，区间型稳健优化模型不但要提高悬置系统的解耦率，当悬置刚度在其名义值附近波动时，还要保证解耦率和固有频率等系统性能的变化区间半径最小，即稳健性最好。

因此，悬置系统区间型稳健优化模型为：

其中，kj—悬置刚度名义值；kjL和kjU分别为下界和上界；kjI=[kj-δ，kj+δ]—悬置刚度值在其名义值附近的波动区间；δ—波动幅度；fiI=fi（k1I，k2I，…klI）和 diI=di（k1I，k2I，…klI）分别是悬置刚度值在其名义值附件波动时，悬置系统各阶固有频率和解耦率的变化区间；mid（diI）和 rad（diI）分别为各解耦率变化区间的中点值和半径[9]，α、β为比例系数，wi、vi为权重。

式（2）的约束条件中含有区间数之间的序关系（即大小关系）问题，文献[6]给出了区间数序关系的一种量化方法，即区间可靠度，其表达式为：

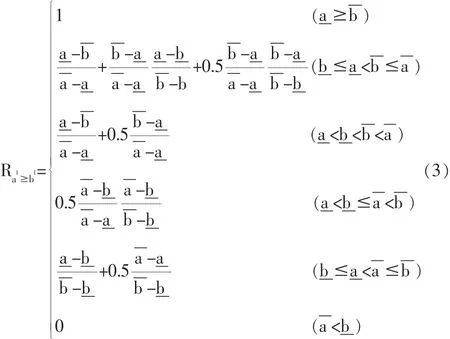
由式（3）中的区间可靠度定义，可以将稳健性优化的区间型约束条件转换为可靠度约束条件。例如，区间型约束条件为fiL≤fiI≤fiU，写成可靠度约束条件为且和分别为满足约束条件i的左、右区间可靠度。因此，式（2）可以转化为式（4）所示的稳健性优化模型：

3 解耦率及频率的变化区间

稳健优化模型中需要计算解耦率及频率的变化区间，当悬置刚度在其名义值附近波动时，通过灵敏度分析可知，悬置系统的固有频率和各方向解耦率均为各悬置刚度值的单调函数。因此，可以采用组合方法求得固有频率和解耦率的精确区间值[9]。

当区间变量取端点值时，f（k1I，k2I，…knI）的所有可能取值为：

其中，ej=L，U，j=1，2，…，l，m=1，2，…2l。

4 算例

图2为某机床伺服电机悬置系统（SMMS），电机坐标系G0－XYZ的原点G0位于电机质心，X轴与电机轴同向，Z轴垂直曲轴向上，Y轴由右手法则确定。将悬置简化成沿其三个弹性主轴方向具有刚度和阻尼的元件[1]，橡胶悬置阻尼很小，可忽略阻尼。以悬置的3个弹性主轴方向建立悬置局部坐标系（LCS）oi-uiviwi，悬置的三个弹性主轴分别用 ui，vi和 wi表示（i=1，2，…，n，n 为悬置个数）。

6个固有频率的约束范围分别为5～30Hz，要求Z轴和Roll方向的解耦率高于90%，其它方向的解耦率高于80%。假设kj可以在其初值kj附近变化±30%。

4个悬置的初始刚度值及优化刚度值见表2。

图2 电机悬置系统示意图Fig.2 Simplified model of the SMMS

表2 悬置初始及优化静刚度（N/mm）Tab.2 Original and optimized static stiffness of the mounts（N/mm）

表3给出了悬置系统初始方案在各方向的频率和解耦率，解耦率的计算方法详见文献[1]。由表3可知，除Y方向以外，该悬置系统的解耦率普遍较低，意味着各方向的耦合振动较严重。

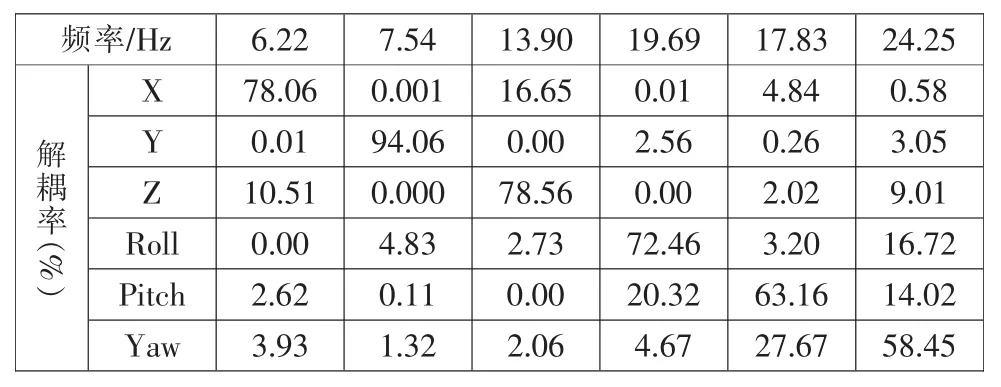
表3 悬置系统固有频率和解耦率的初始值Tab.3 Origin frequency and decoupling ratio of the SMMS

假设式（4）中所有频率约束条件的左、右区间可靠度均要求为1.0。优化结束后，表4给出了当确定性优化和区间优化所得到刚度优化值波动时，解耦率的变化区间。一般地，悬置刚度值的波动δ幅度约为10%～15%，文中对波动幅度为10%和15%两种情况进行讨论。

从表4可知，区间优化和确定性优化均可提高悬置系统的解耦率。由于在稳健优化模型中考虑了解耦率的稳健性要求以及设定频率约束条件的区间可靠度为1.0，所以导致解耦率稍有降低。由表4可以看出，波动幅度δ增大时，解耦率的区间半径增大，即不确定性增大。

表4 优化后悬置系统解耦率的变化范围（%）Tab.4 Intervals of the optimized decoupling ratios（%）

表5给出了当确定性优化和区间优化所得到刚度优化值波动时，频率的变化范围，以及在确定性优化和稳健优化的刚度名义值处各约束条件的左、右区间可靠度。可以看出，波动幅度δ增大时，频率的区间半径增大，即不确定性增大。将悬置刚度值看作正态分布的随机变量，对优化结果进行σ水平分析，可以看出，频率约束的左右区间可靠度越大，σ水平越高，稳健性越好，反之越低。

表5 优化后悬置系统频率变化范围及频率约束的左右区间可靠度和水平Tab.5 Intervals of the optimized decoupling ratios and the interval reliability degrees and levels of the optimized SMMS

当稳健优化得到的刚度优化值有所波动时，各约束条件左、右区间可靠度较确定性优化有较明显增大，表明频率约束的稳健性有较大幅度的提高，在Z和Roll方向尤为明显，相应地，σ水平也有明显提高。这表明，文中给出的表征频率稳健性的度量指标是合理的，稳健优化结果是有效的。

5 结束语

提出的区间型稳健优化方法不仅能有效提高悬置系统各方向的解耦率，与确定性优化方法相比，稳健优化方法还可以较大幅度地提高频率和解耦率的稳健性。

稳健优化方法在优化过程中考虑到设计变量的波动对优化结果的影响，在不易获得或很难精确获得不确定参数的统计特性或模糊信息的情况下，采用该方法可以有效提升悬置系统性能的稳健性。