热泵干燥条件下刺参有效扩散系数的研究

(1 烟台大学海洋学院 烟台 264005； 2 天津大学机械工程学院 天津 300072； 3 烟台大学土木学院 烟台 264005)

刺参是目前我国海水养殖中最活跃、发展最快的水产品，为了满足干制品质量和节能的要求，新型热泵干燥方式已开始应用于刺参干制加工中[7-9]。确定刺参在热泵干燥过程中的Deff对于研究刺参的干燥动力学特性、优化干燥工艺、深入研究刺参内部的干燥传质特性都具有重要意义。但刺参本身为圆筒状，两端稍细，体背有疣足，形状不规则，从尺寸上也不能看作是无限长圆柱体，故不能用解析方法确定刺参的Deff。本文将基于有限元模型的Deff确定方法引入刺参热泵干燥研究，深入探讨热泵干燥条件下刺参Deff的影响因素和变化规律。

1 干燥数学模型

以刺参为对象建立干燥数学模型。建模中，假设刺参为均匀对称的不等边椭球形，取其1/4进行建模，如图1所示，上方锥形突起为疣足。

图1 刺参建模对象Fig.1 The modeling object of sea cucumber

刺参干燥模型是描述其内部水分扩散的非稳态传质模型，该模型由3部分组成：控制微分方程、边界条件和初始条件。基于菲克第二定律[10-11]得到控制微分方程：

(1)

边界条件：

(2)

初始条件：

X(x,y,z,0)=X0

(3)

式中：X为局部干基含水率(层内水分质量/层内干基质量)，%；X0为刺参初始干基含水率，%；τ为干燥时间，s；kc为对流传质系数[11]，m/s；Xe为刺参达到平衡状态时的干基含水率，%。

刺参在热泵干燥过程中，随着体内水分不断脱除，整体逐渐收缩。收缩率随干基含水率的变化如下[12]：

ε=a+bX

(4)

式中：ε为收缩率；a，b为方程系数，根据实验数据拟合获得。

方程(1)～(4)组成了考虑刺参干燥收缩的数学模型。为了分析刺参干燥收缩对Deff的影响，本文还建立了不考虑刺参干燥收缩的数学模型进行对比分析，该模型由方程(1)～(3)组成。

2 刺参热泵干燥实验

2.1 实验装置

干燥用热泵装置为自制，工作原理如图2所示。该实验系统包括热泵回路和干燥空气回路两部分。热泵回路由直流变频压缩机1、冷凝器2、储液器3、节流阀4、蒸发器5及相应连接管道组成，干燥空气回路由风机6、干燥箱7、风量调节阀8、旁通风量调节阀9和相应连接风道组成。热泵回路的工作原理同文献[13-15]。在干燥空气回路中，干燥空气进入冷凝器吸热后温度升高，在风机驱动下进入干燥箱加热刺参，吸收水分后流出干燥箱，经风量调节阀后，一路经蒸发器除湿，另一路经旁通风量调节阀流出，两路空气混合后再进入冷凝器加热，完成空气回路循环。调节旁通风量调节阀开度可以实现干燥空气温度和湿度的变化。通过实验测试，本热泵实验台的性能系数(加热量/输入电量)可达3.2～3.6。

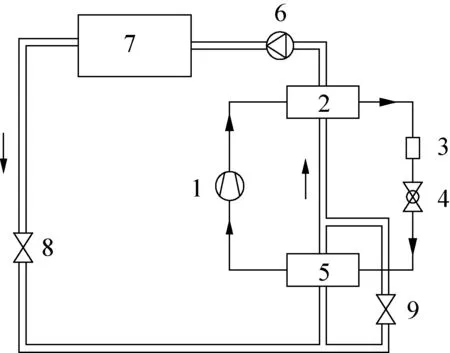
1压缩机；2冷凝器；3储液器；4节流阀；5蒸发器；6风机；7干燥箱；8风量调节阀；9旁通风量调节阀。图2 热泵干燥实验原理Fig.2 The principle of heat punp drying experiment

2.2 实验材料

实验所用刺参来自烟台某市场，经去除内脏、煮沸、沥干表面水分处理后，质量为(18±4.5)g，长、短半径分别为(90±5) mm、(29±4) mm，赤道半径为(29±4) mm，初始干基含水率为643%±76.7%。

2.3 实验方法

每组实验选择10个大小相近的刺参样品，用电子天平称取质量。实验前先预热热泵，调节压缩机频率和旁通风量调节阀达到设定干燥温度后，将刺参单层均匀平铺在托盘中放入干燥箱，每隔20 min取出用电子天平称取质量，用游标卡尺测量并记录长、短半径和赤道半径，当干燥至含水量基本稳定时停止实验。

实验中，测得干燥空气流速为0.8 m/s，干燥温度为35 ℃±1 ℃、40 ℃±1 ℃、45 ℃±1 ℃，相对湿度为17%±1%、14%±2%、25%±1%。

2.4 指标参数测量

2.4.1干基含水率

干燥结束后，将刺参置于红外干燥箱内，设定温度为103 ℃，根据食品水分测定国家标准[16]将刺参完全干燥，作为全干质量，再由实验过程中测得的瞬时质量计算得到每个测量时刻的平均干基含水率：

(5)

2.4.2收缩率

根据测得的刺参长、短半径和赤道半径计算刺参体积，代入式(6)计算收缩率：

(6)

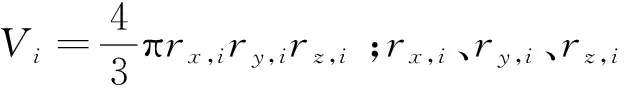
3 Deff计算模型

根据是否考虑Deff随干燥温度和干基含水率的变化，分别提出了两种Deff计算模型，用于干燥数学模型中Deff的计算。

M1模型：不考虑Deff随干基含水率的变化，即在给定干燥条件下，

Deff=const

(7)

运用该模型得到不同干燥温度的Deff后，拟合获得其随干燥温度的变化，即Arrhenius公式：

(8)

式中：D0、Ea为待定系数；R为摩尔气体常数，J/(mol·K)；t为干燥温度，℃。

M2模型：考虑Deff随干基含水率的变化，即在给定干燥条件下，

Deff=a0X+b0

(9)

式中：a0，b0为待定系数。

有学者研究得到了稻谷、糙米、玉米、小麦、蔬菜等物料的Deff随干基含水率的变化[2]，但对刺参的研究很少。将M2模型代入干燥数学模型，得到不同干燥温度的Deff后，再拟合得出刺参的Deff随干燥温度与干基含水率的变化，表示为修正的Arrhenius公式：

(10)

式中：aj(j=1,2,3,4)，bk(k=1,2)为待定系数。

4 基于有限元模型的Deff确定方法

(11)

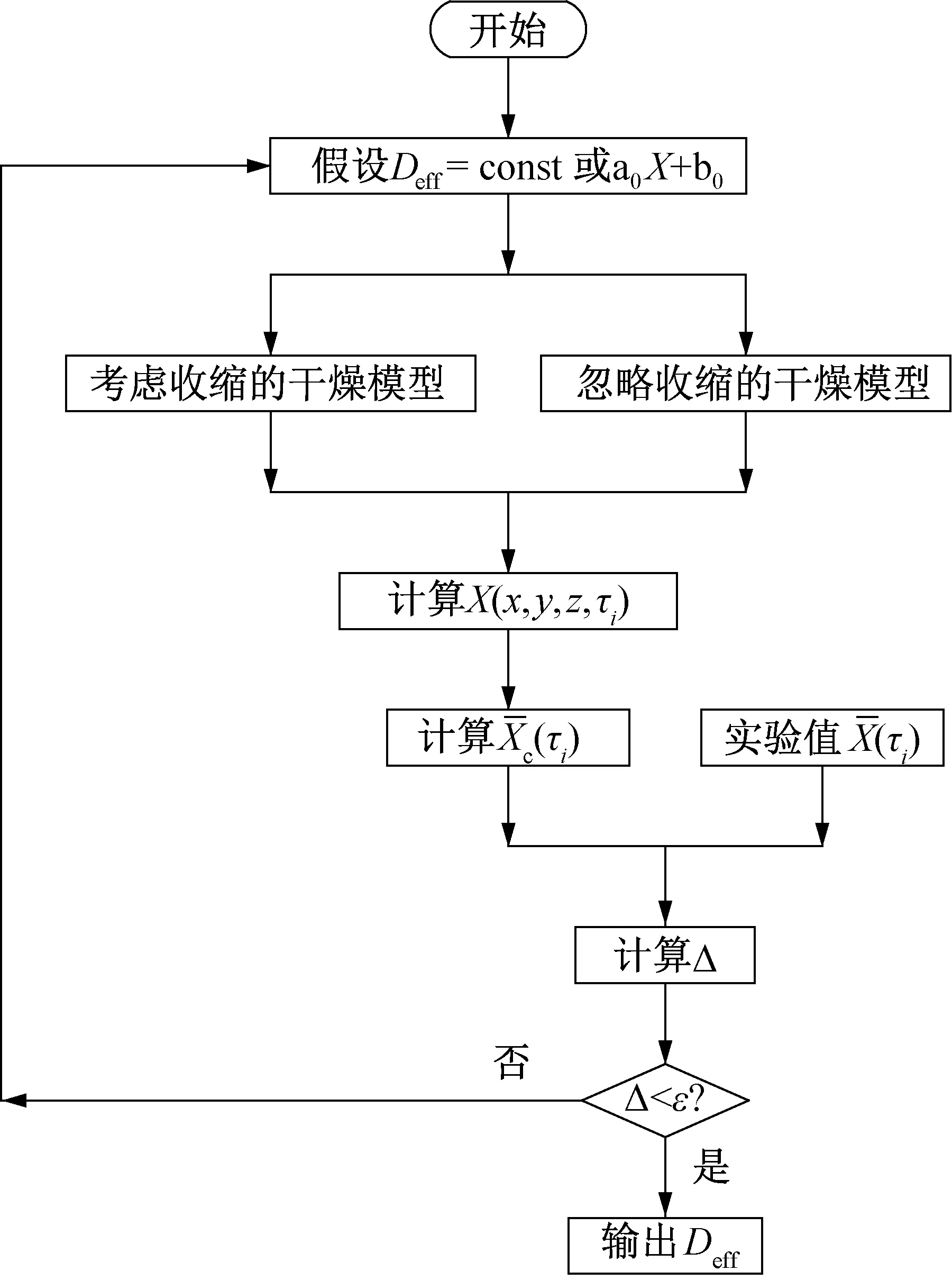
图3 所示为基于有限元模型的Deff确定方法流程图Fig.3 The flow chart of determination of Deff based on FME model

按照上述Deff计算方法，在流程图中，分别采用M1和M2模型后，通过迭代可得Deff为常数和随干基含水率变化的两种结果。

为了研究干燥数学模型对Deff的影响，将考虑与忽略收缩的干燥数学模型分别代入计算，得到对应的Deff，分别称为考虑收缩与忽略收缩的Deff(以下称为模型输出值)。利用上述方法，计算得到各干燥条件下的Deff，再通过MATLAB软件的最小二乘法[17]，辨识出式(8)与式(10)中D0、Ea、aj、bk等系数值，得到计算Deff的公式，获得Deff随干燥温度t和干基含水率X的变化。

5 结果与分析

上述模型中，按照是否考虑刺参收缩以及选用哪个刺参Deff模型(M1或M2)，可分别计算得到考虑收缩且Deff随t变化、忽略收缩且Deff随t变化、考虑收缩且Deff随t和X变化、忽略收缩且Deff随t和X变化4种情况下的刺参Deff，并进行对比分析。

根据M1模型，同一温度下刺参内部的Deff为常数。图4所示采用M1模型得到的刺参Deff随t的变化。可以看出，在考虑收缩情况下，随着t由35 ℃升至45 ℃，Deff从7.9×10-10m2/s增至16.4×10-10m2/s，增加了一倍多。说明刺参的Deff随t的增加而增加。由图4还可以看出，在3种温度下，考虑刺参收缩的Deff均低于忽略收缩情况，分别降低了11%、14.5%、8.7%。原因是刺参干燥过程中有较大收缩，导致不考虑收缩建模中的刺参尺寸大于实际情况，需要更大的Deff才能与X动态实验数据相符。由此可知，采用基于有限元模型确定Deff时，建模必须考虑收缩引起的几何尺寸变化，否则会产生较大偏差。

图4 热泵干燥条件下，Deff随干燥温度的变化Fig.4 Variation of effective diffusivity with drying temperature under heat pump drying

为了便于计算Deff，将上述模型输出值拟合为Arrhenius公式：

忽略收缩：

(12)

考虑收缩：

(13)

由图4可以看出，用式(12)～(13)计算得到的拟合值与模型输出值吻合较好，忽略与考虑收缩时的相关系数[17]分别为0.999和0.994。

图5所示为不同热泵干燥条件下，采用M2模型得到的刺参内部Deff随t和X的变化。可以看出，在3种热泵干燥温度下，X从500%降至50%时，Deff分别由12.2×10-10、15.4×10-10、22.1×10-10m2/s降至6.9×10-10、8.7×10-10、13.7×10-10m2/s，均降低了约40%。说明X越高，刺参内部水分扩散更快，反之越慢。在t影响方面，当t从35 ℃升至45 ℃后，Deff增加了80%～93%，且X越低增加值越大。

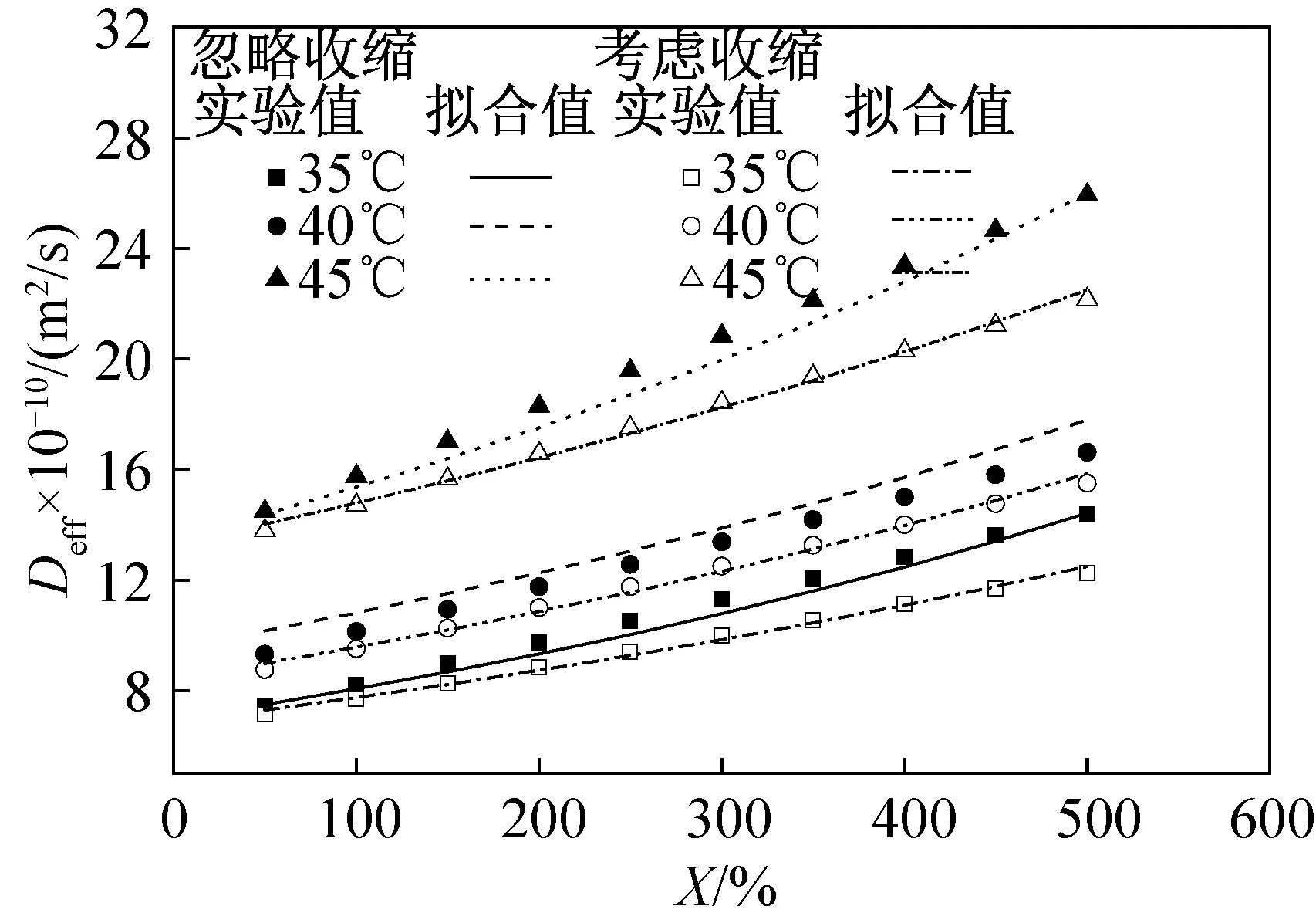
图5 热泵干燥条件下，Deff随干燥温度和干基含水率的变化Fig.5 Variation of effective diffusivity with drying temperature and dry-based moisture content under heat pump drying

为了便于计算Deff，将上述模型输出值拟合为修正Arrhenius公式：

忽略收缩：

(14)

考虑收缩：

(15)

由图5可以看出，用修正Arrhenius公式(14)～(15)计算的Deff拟合值与M2模型输出值之间吻合也较好，忽略与考虑收缩时的相关系数分别为0.993和0.999。

与图4类似，由图5也可以看出考虑收缩比忽略收缩得到的Deff要小，相对偏差范围为3.9%～14.6%。再次证明了模型中干燥收缩对Deff计算具有重要影响。

拟合得到描述Deff对t和X变化的公式(12)～(15)后，将其代入干燥数学模型，可得到不同情况下刺参X的动态变化，如图6～图8所示。可以看出，不同Deff模型计算得到的刺参X均随干燥进行而逐渐下降，与实验测试数据变化趋势一致。但4种模型中，忽略收缩的Deff模拟得到的X与实验测试数据偏差较大。如在(35±1) ℃干燥条件下，干燥初期模拟值明显小于实验值而后期则高于实验值，而在(40±1) ℃和(45±1) ℃干燥条件时，刺参含水率拟合值均在干燥后半段明显高于实验值，且在(40±1) ℃干燥条件时，高出实验值情况最严重。在上述3种干燥条件下，考虑收缩的Deff模型模拟得到的X与实验值吻合最好，尤其考虑Deff随t和X变化时的模拟值与实验值一致性更好，相关系数分别为0.995、0.994、0.996。而只考虑Deff随t变化时的模拟值与实验值的相关系数分别为0.993、0.991、0.994。由此可知，考虑收缩且Deff随t和X变化时，模拟精度更高，与实验数据更吻合，在干燥研究中应优先推荐使用。

图6 (35±1) ℃热泵干燥下干基含水率的变化Fig.6 Variation of dry-based moisture content with drying time under heat pump drying (t=(35±1) ℃)

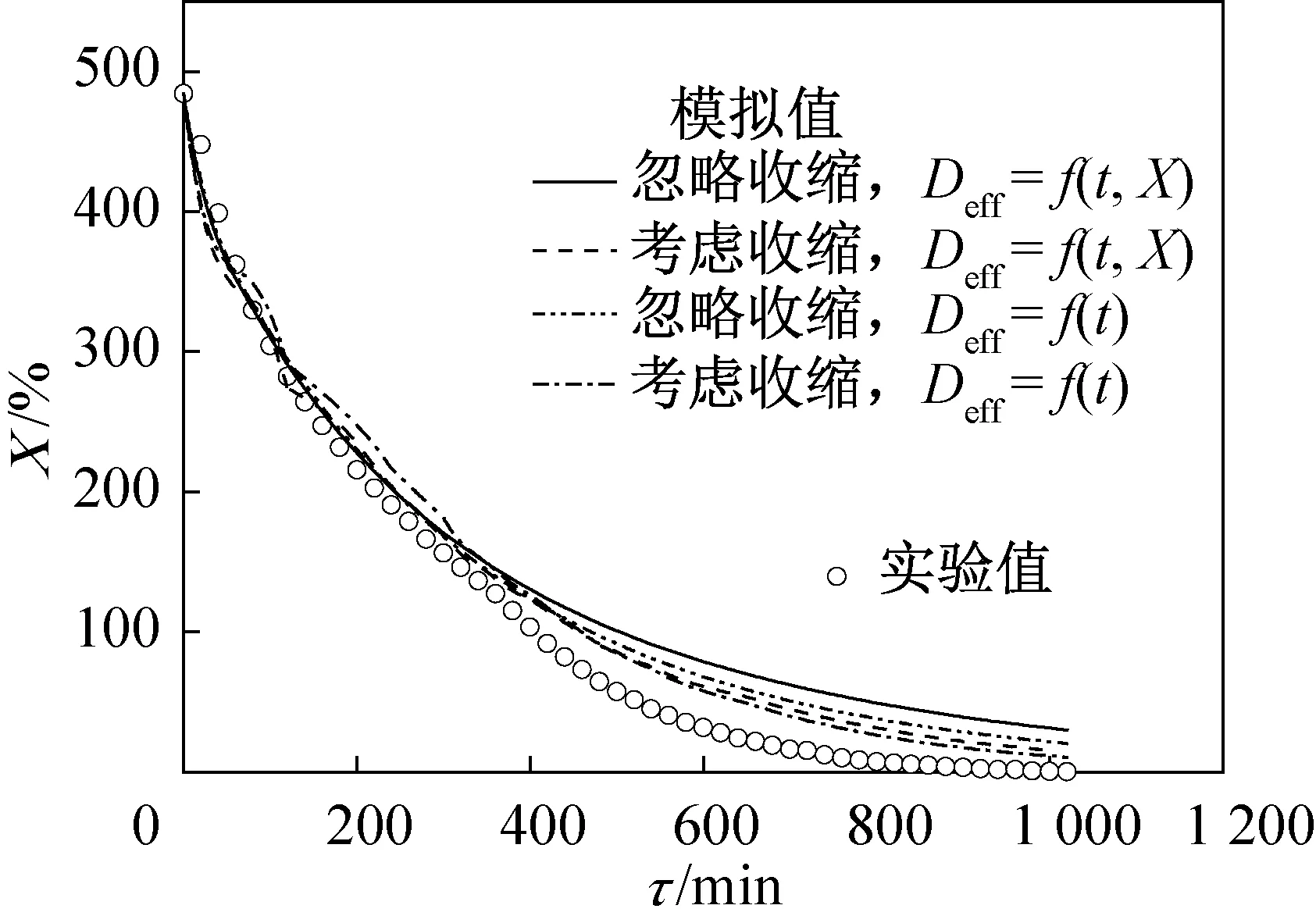
图7 (40±1) ℃热泵干燥下干基含水率的变化Fig.7 Variation of dry-based moisture content with drying time under heat pump drying (t=(40±1) ℃)

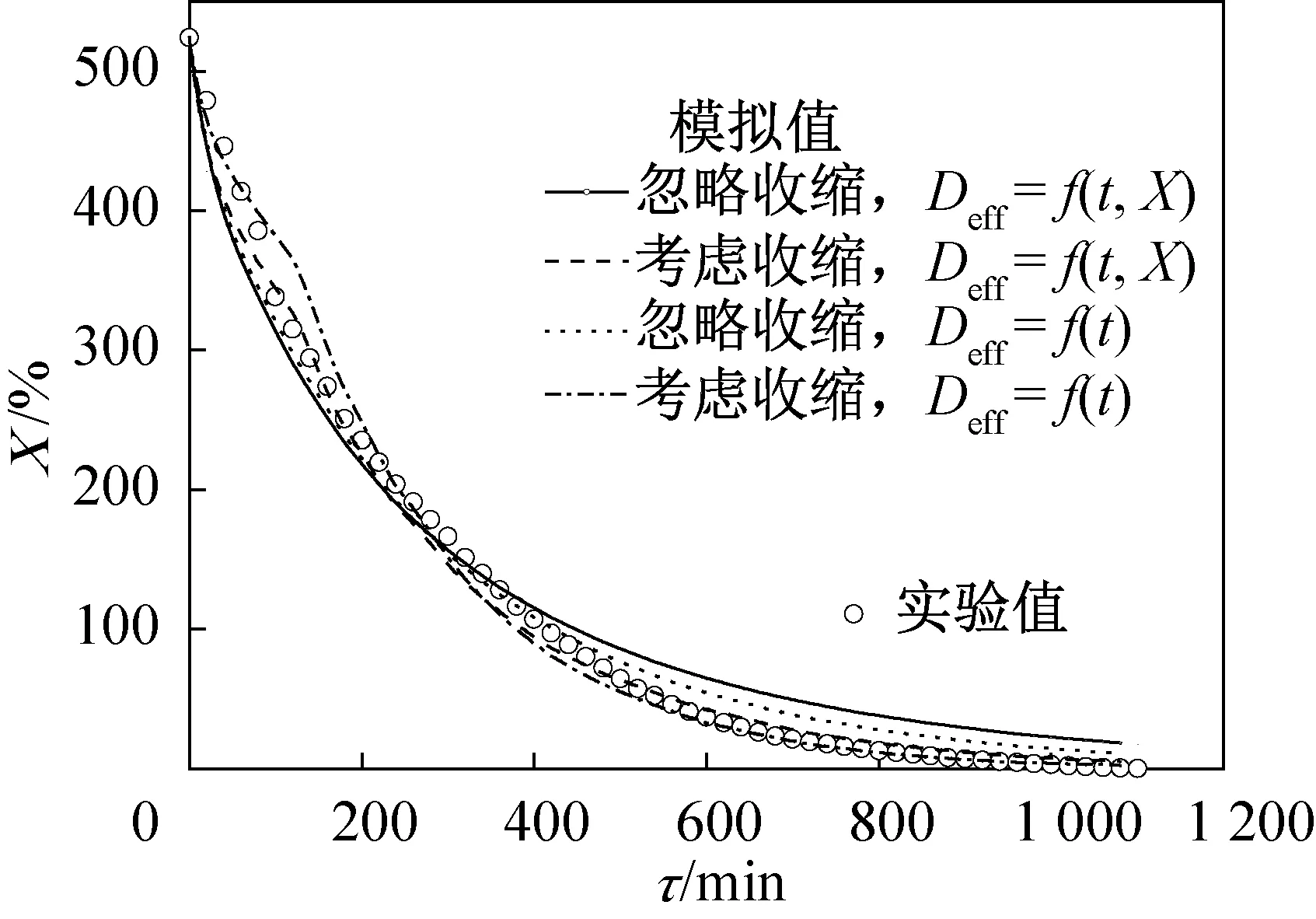
图8 (45±1) ℃热泵干燥下干基含水率的变化Fig.8 Variation of dry-based moisture content with drying time under heat pump drying (t=(45±1) ℃)

图9所示为在(40±1) ℃热泵干燥温度下，不同时刻刺参内部Deff的分布。可以看出，干燥进行至1、5、15 h时，刺参内部Deff范围分别为8.2×10-10～14.6×10-10m2/s，8.1×10-10～12.6×10-10m2/s和8.0×10-10～8.9×10-10m2/s。刺参内外Deff差值由6.4×10-10m2/s降至0.9×10-10m2/s。刺参内部Deff由内向外逐渐降低，靠近中心处由于X较高，对应的Deff较大，而在刺参外表面处，由于X较低，Deff最小。由图9还可以看出，随着干燥的进行，刺参外形尺寸逐渐减少，对应上述3个干燥时刻的疣足尖部最大尺寸由1.8 cm依次缩小至1.6 cm和1.5 cm，最大缩小率达到16.7%，尺寸变化较大，说明建模不能忽略收缩效应，否则计算结果将产生较大偏差，图4～图8中两种情况下的数值偏差也证明了上述观点。

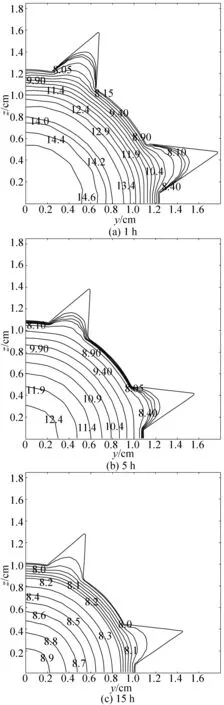
图9 不同时刻刺参内部扩散系数的分布Fig.9 Effective diffusivity distribution inside the sea cucumber in different drying times

6 结论

本文探讨了基于有限元模型确定扩散系数Deff在刺参热泵干燥研究中的应用，实验测试了3种不同热泵干燥温度t下的刺参干基含水率X变化，建立了考虑收缩的刺参热泵干燥模型和Deff模型，通过X模拟值与实验值对比优化获得Deff，并对比分析收缩变形、t和X因素对刺参Deff的影响。得到如下结论：

1)刺参的Deff随t的增加而增加，t从35 ℃升至45 ℃后，Deff增加了1倍多。

2)X对Deff具有较大影响。在3种t下，Deff均随着X的降低而降低，X由500%降至50%时，Deff降低40%左右。

3)Deff研究中应考虑收缩变形的影响，且考虑收缩的Deff均低于忽略收缩情况，对应M1模型的Deff相对偏差范围为8.7%～14.5%，而M2模型的Deff相对偏差范围为3.9%～14.6%。采用忽略收缩的干燥模型模拟得到的X与实验测试数据偏差最大，而考虑收缩的干燥模型模拟得到的X与实验值吻合最好，尤其考虑Deff随t和X变化时，模拟值精度更高，相关系数超过0.994。

4)在刺参内部，Deff范围随干燥进行逐渐减小，且按由内向外逐渐降低的规律分布，越靠近中心Deff越大。从1 h至15 h，内外Deff差值由6.4×10-10m2/s降至0.9×10-10m2/s，中心处Deff则由14.6×10-10m2/s降至8.9×10-10m2/s。

本文受山东省自然基金(ZR2014EL029)和天津市自然科学基金重点(16JCZDJC33900)项目资助。(The project was supported by Shandong Provincial Natural Science Foundation, China (No. ZR2014EL029) and Tianjin Provincial Key Natural Science Foundation of China (No. 16JCZDJC33900).)