基于随机结构的无乘法无限冲激响应数字滤波器设计方法
冯帅栋,陈立家,刘名果
(河南大学 物理与电子学院,河南 开封 475000)
0 引言
数字滤波器是一种信号处理装置,它能够降低噪声、消除干扰,因此被广泛应用于电视雷达、通信传输、生物医学等各个领域[1-3]。传统的无限冲激响应(Infinite Impulse Response, IIR)数字滤波器结构中包含乘法器,这影响了滤波器的运算速度,增加了硬件结构的复杂程度[4]。因此,许多学者开始进行无乘法IIR数字滤波器的研究。
在文献[5-7]中,IIR数字滤波器的无乘法设计是基于经典的滤波器结构(级联型、并联型等)将乘法器的系数转换为二次幂的和或差,然后通过乘法块进行实现。例如乘法器系数10转换为乘法块是23+21,这种二次幂的转换通常利用CSD(Canonic Signed Digit)码进行实现,但是通过这种方法设计的无乘法IIR数字滤波器存在系数量化误差和结构固定的问题,并不能满足数字滤波器的性能要求。为了优化无乘法IIR数字滤波器的设计方法,一些学者开始尝试利用演化算法对无乘法IIR数字滤波器进行设计。在文献[8]中,一种新的无乘法IIR滤波器设计方法被提了出来。该方法首先对加法器的个数进行设定;然后计算出包含相应个数加法器的所有回路,并且以这些回路为种群;最后利用进化的变邻域搜索(Evolutionary Variable Neighborhood Search, E-VNS)算法对这些回路进行元器件(移位器、延时器、反相器)插入操作,直到元器件的插入对回路的改进没有效果为止。这种方法虽然在传统设计基础上作了改进,但是计算量非常大并且需要大量的元器件去实现,这增加了滤波器结构的复杂度;而且E-VNS算法搜索精度低、耗时长且容易早熟。在文献[9]中,提出了一种加入成功父代选择框架的差分进化(Differential Evolution with a Successful-Parent- Selecting Framework, SPS-DE)算法。这种方法将成功的父代个体存储在一个库里,当个体进化停滞时,成功的父代个体从库里被选择出来替换掉停滞的个体,这样可以帮助个体逃离不光明的区域以促进种群收敛,有效地平衡了种群探索与开发的能力。鉴于SPS-DE出色的性能,本文将其运用到无乘法IIR数字滤波器设计中。
为了设计一种满足结构多样性要求、性能优良的无乘法IIR数字滤波器,本文提出了一种基于随机结构的无乘法IIR数字滤波器设计方法。本方法利用加入移位器的子系统直接设计无乘法数字滤波器,不存在对乘法器系数的量化,然后通过SPS-DE对结构进行优化,设计的滤波器具有满足要求的随机结构,并取得了较好的滤波器性能。最后,本文分别利用SPS-DE、遗传算法(Genetic Algorithm, GA)[10]、粒子群算法(Particle Swarm Optimization, PSO)[11]、差分进化(Differential Evolution, DE)算法[12]、多精英指导拥有转移机制的差分进化算法(Adaptive Multiple-Elites-guided Composite Differential Evolution algorithm with a shift mechanism, AMECoDEs)[13]进行了无乘法IIR滤波器设计,对算法的性能进行了分析,然后将本文方法和现有的无乘法滤波器设计方法进行了对比,对本文方案的有效性进行了验证。
1 无乘法IIR数字滤波器结构的生成
IIR数字滤波器可以通过差分方程表示:
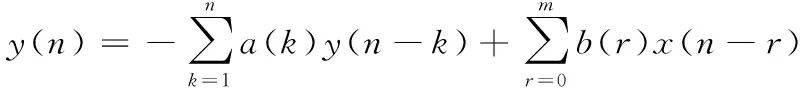
(1)
从式(1)可以看出,数字滤波器由加法器、乘法器和延时器这些基本的元器件构成。在本文中,提出的方法利用移位器设计了一种稳定的二阶子系统,通过二阶子系统对无乘法IIR滤波器进行设计。二阶子系统由4个移位器,2个延时器和3个加法器构成,它的结构如图1所示。其中a、b、c、d代表4个移位器,z-1表示延时器,3个黑点代表加法器,箭头代表了信号流向。
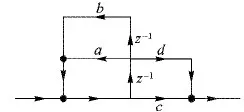
图1 二阶子系统
1.1 生成指令
本文将二阶子系统视作基本单元,从滤波器系统的输入端开始按照生成指令依次添加子系统直到一个完整滤波器结构的形成,生成指令控制着子系统如何被添加到初始的滤波器系统中。
每一个生成指令由4部分构成:指令类型(C)、子系统输入端编号(I)、子系统输出端编号(O)、子系统的参数(P),这4部分的值随机产生。其中指令类型有四种:连接新活动点(C1)、连接已存在的点(C2)、连接系统的输入端(C3)、连接系统的输出端(C4),每种指令类型的产生概率可以自由设置。系统的输入端被定义为第一个活动点,依照指令类型,子系统的输入端和输出端被分别连接到相应编号的节点。执行C1和C4指令时,子系统的输入端被连接到当前的活动点,输出端相应的被分别连接到新的活动点和系统的输出端。执行C2和 C3指令时,子系统的输入端相应的被分别连接到已存在的点和系统的输入端,而输出端被连接到当前的活动点。C1指令执行后,活动点改变,新活动点的编号为先前的活动点编号加1;C2,C3和C4指令执行后,活动点不变。生成指令如图2所示。

图2 生成指令格式
Fig. 2 Generation instruction format
1.2 指令序列
所有的生成指令按其产生顺序依次连接,就形成了一个指令序列,每一个指令序列代表了一个无乘法IIR数字滤波器的结构。表1给出了一个指令序列的示例。

表1 指令序列
从表1可以看出,这个指令序列由5个生成指令组成。其中表格第1列的ID代表生成指令的序号;表格的第5列代表了子系统中4个移位器的参数值,数字与字母的组合代表一个移位器,如:+L2表示一个正数向左移动2位,-R3表示一个负数向右移动3位;表格的第6列表示子系统的编号,如:第一条生成指令对应的子系统,其编号为S1。
对应表1中指令序列的无乘法数字滤波器结构被显示在图3中。其中x(n)和y(n)分别代表无乘法滤波器的输入端和输出端,它们被分别编号为1和0;箭头代表信号的流向;节点3有一个输出和多个输入,它代表一个加法器。这个无乘法数字滤波器由5个子系统构成,共包含了20个移位器、10个延时器和16个加法器。
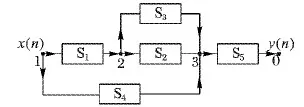
图3 对应表1的无乘法数字滤波器结构
2 SPS-DE优化无乘法IIR数字滤波器的结构
通过生成指令生成无乘法IIR数字滤波器之后,对代表滤波器结构的指令序列进行编码,然后利用SPS-DE对它的结构进行优化。滤波器的频率响应可以通过传输函数获得,适应度通过对设计的数字滤波器的频率响应与目标频率响应在采样点上的均方差的计算来评估。公式如下:
(2)
其中:N为采样频率,D(Ki)为设计的滤波器频率响应,T(Ki) 为目标滤波器的频率响应。
SPS-DE优化结构的流程如下。
首先对种群进行初始化,每一个个体对应一个指令序列。然后利用适应度函数对个体进行评估,如果满足目标条件则输出最佳个体;否则,执行下一步对种群进行变异操作,SPS-DE算法采用差分策略从种群中随机选出3个不同的个体进行变异操作。然后接着对变异后的种群进行交叉操作,本文采用单点交叉,也就是在两个不同个体的相同编号节点间进行交叉,实现两个滤波器之间的结构互换。完成交叉后,对种群进行选择,其中较好的个体进入下一代继续进行优化。
因为SPS-DE加入了SPS (Successful-Parent-Selecting)机制,所以种群每一次迭代完成后,就会检测种群是否停滞。通过计算第g代种群中近来连续未成功进化个体的数目对停滞程度进行评估。公式如下:
(3)
其中:qi(g)、qi(g+1)分别表示第g代和第g+1代种群中近来连续未成功进化个体的数目;Xi(g)代表第g代第i个个体,F(Xi(g))表示其适应度;Ui(g)表示对Xi(g)进行交叉后生成的实验向量,F(Ui(g))表示其适应度。如果qi(g+1)超过了一个不可接受的值Q,此时种群被定义为停滞。种群停滞时,SPS机制会从存储成功父代个体的库里选择成功的个体对停滞的个体进行替换。成功父代个体p(g)的来源被表示如下:
(4)
其中:Pg代表第g代种群,A代表近来连续成功升级个体的库,Q代表停滞容忍度。
无乘法IIR滤波器结构优化的具体步骤如下:
步骤1 首先进行种群初始化,随机产生M个代表无乘法滤波器结构的指令序列编码,每一个指令序列代表种群中的一个目标向量。
步骤2 对种群中的每个目标向量进行适应度评价,然后判断是否达到迭代次数。若满足,则停止计算并输出最优的个体;否则,执行步骤3。
步骤3 从种群中选择出不同的个体执行变异操作,生成变异向量。
步骤4 对变异后的种群执行交叉操作产生实验向量。
步骤5 对目标向量和实验向量进行适应度评估,从中选择出最佳的个体进入下一代。
步骤6 判断种群进化是否出现停滞并且启动SPS机制,然后返回步骤2。
3 实验仿真与分析
通过本文的方法设计一个通带截止频率为0.4π,阻带截止频率为0.6π的低通无乘法IIR数字滤波器,然后利用Matlab进行仿真。在本文中,设计了一些对比实验对本文方法的有效性进行了验证。
3.1 移位器位数的对比
为了分析移位器参数范围的大小对无乘法IIR数字滤波器性能的影响,本文设计了具有不同位数范围的无乘法IIR滤波器进行对比。移位器的位数被分别设置为5、6、7、8、9、10、11,滤波器的其他设计参数和表2一致,为了平衡4种连接方式的概率,其中C1、C2、C3、C4的概率被设置为等概率。然后分别在每种情况下进行100组测试,将每种情况下最好的实验结果进行了对比。
如图4所示,这些无乘法IIR滤波器的通带波纹都在2.7 dB以内。在过渡带区域,5位无乘法滤波器的幅频响应有最快的衰减,在0.6π时已衰减至-64 dB,而6位、7位、8位、9位、10位、11位的无乘法滤波器在0.6π时分别衰减到-58 dB、-45 dB、 -47 dB、-40 dB、-30 dB 和 -36 dB。在阻带区域,5位~11位的无乘法滤波器的阻带最大衰减分别为-64 dB, -58 dB, -45 dB, -47 dB, -40 dB, -30 dB 和-36 dB。整体来看,当移位器的位数较小时,无乘法IIR滤波器有较好的性能,这是因为当位数较小时,量化误差也相对较小。

图4 不同位数的无乘法IIR滤波器的幅频响应
3.2 不同算法设计无乘法IIR滤波器的对比
为了分析不同算法对无乘法IIR数字滤波器结构优化的效果,本文分别利用SPS-DE、AMECoDEs、DE、GA 和 PSO设计了一个5位的无乘法IIR滤波器进行对比,滤波器的其他设计参数和表2一致。为了对比的合理性,每种算法的种群数目都设置为100,迭代次数设置为10 000代,算法的其他参数都是在其算法性能最优的情况下进行设置,这5种算法的仿真参数如表3所示,其中:“—”表示没有参数值。然后在每种算法下分别进行了100组实验,对每种算法设计的最优结果进行对比。
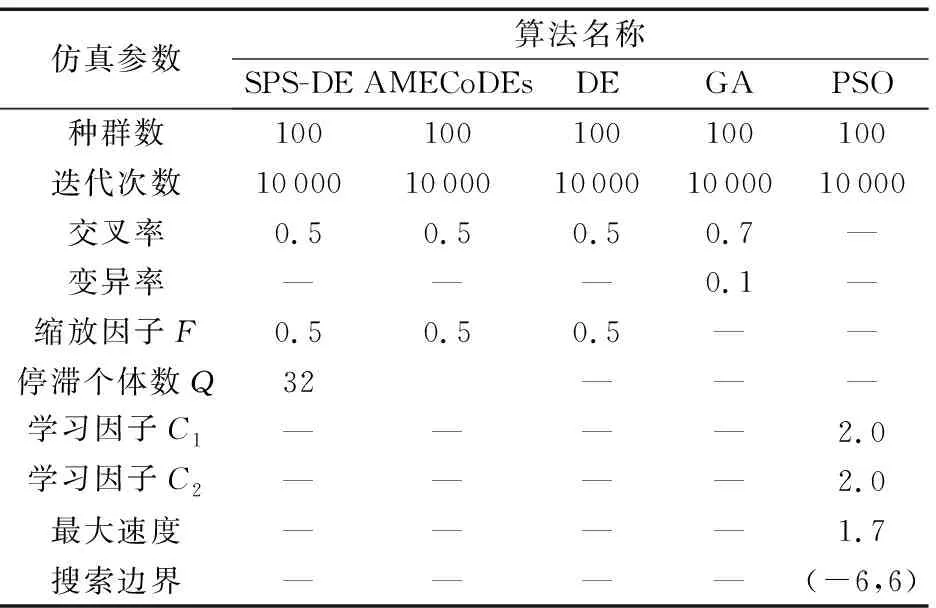
表3 不同算法的仿真参数
正如图5所示,利用这几种算法设计的无乘法IIR滤波器的通带波纹都在2.7dB以内。在过渡带区域,通过SPS-DE、AMECoDEs、DE、GA和PSO设计的滤波器幅频响应在0.6π时分别衰减至-64 dB、-49 dB、-50 dB、-35 dB和-45 dB。这些滤波器的阻带最大衰减分别为-64 dB、-49 dB、-50 dB、-35 dB和-45 dB。
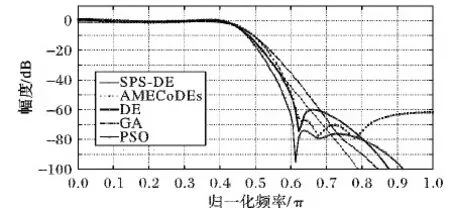
图5 不同算法设计的无乘法IIR滤波器的幅频响应
图6表示每种算法在其算法参数设置最佳情况下的演化曲线,其中SPS-DE收敛最快并最终达到了一个最小值,结果表明利用SPS-DE设计的无乘法IIR滤波器的性能最好。原因是SPS-DE算法加入了成功父代选择框架,有效地平衡了种群的开发和探索能力,避免了种群陷入局部最优,过早收敛。
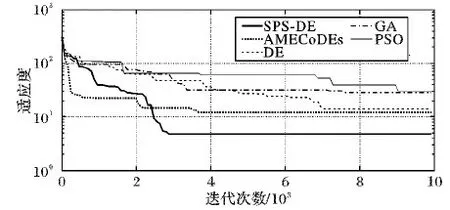
图6 每种算法的演化曲线
3.3 与无乘法FIR数字滤波器的对比
图7是通过等波纹法、最小二乘法、最小P次归一法分别设计的一个通带截止频率为0.4π,阻带截止频率为0.6π的14阶无乘法有限冲激响应(Finite Impulse Response,FIR)数字滤波器,本文设计了一个同样目标的无乘法IIR数字滤波器与之进行对比,滤波器的设计参数和SPS-DE算法参数如表2和表3所示。如图7所示,无乘法FIR滤波器和本文设计的无乘法IIR数字滤波器通带波纹都在1.2 dB以内。在阻带区域,等波纹法、最小二乘法、最小P次归一法设计的无乘法FIR滤波器的阻带最大衰减分别为-32.5 dB,-24.47 dB,-36.7 dB,本文设计的无乘法IIR数字滤波器的阻带最大衰减为-64 dB。通过数据分析可以看出,本文设计的无乘法IIR数字滤波器性能好于无乘法FIR数字滤波器,这是因为FIR滤波器结构中没有反馈回路,而IIR结构中含有反馈回路,其幅频精度较高。因此,在同等条件下,无乘法IIR滤波器性能较好。
3.4 与结构设计无乘法IIR滤波器方法的对比
文献[8]设计了一个通带截止频率为0.7π,阻带截止频率为0.906 9π,阻带最大衰减为-50 dB的无乘法IIR滤波器,滤波器由20个延时器、40个移位器、11个加法器和20个反相器构成。本文设计了一个相同目标的IIR滤波器与文献[8]进行对比,移位器位数设置为5,其他的滤波器设计参数和表2一致。利用本文方法设计的无乘法IIR滤波器包含了14个延时器、28个移位器、21个加法器和11个反相器,元器件总数目比文献[8]少了17个。图8和图9分别表示文献[8]设计的无乘法IIR滤波器和本文设计的无乘法IIR滤波器的幅频响应。文献[8]设计的无乘法滤波器和本文设计的无乘法滤波器的幅频响应通带波纹分别为2 dB和 1.14 dB。在过渡带区域,本文设计的滤波器幅频响应在0.9π时已经下降到了-70.2 dB,而文献[8]设计的滤波器幅频响应仅下降到-50 dB。文献[8]设计的滤波器和本文设计的滤波器幅频响应的阻带最大衰减分别为-50 dB和 -70.2 dB。通过以上数据分析来看,在通带截止频率和阻带截止频率相同的情况下,本文方法设计的无乘法IIR数字滤波器通带波纹减小了43%,阻带最大衰减下降了40.4%,而且该方法使用较少个数的元器件实现了优良的滤波器性能,这降低了滤波器结构的复杂度,实验进一步表明了本文方法的有效性。
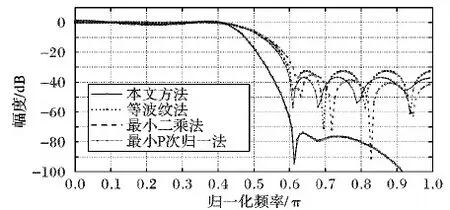
图7 与无乘法FIR数字滤波器的对比
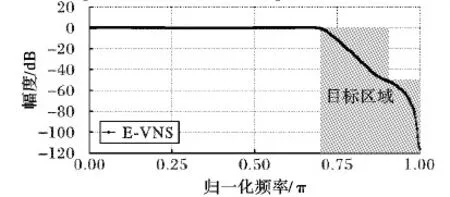
图8 文献[8]中设计的无乘法IIR数字滤波器的幅频响应

图9 本文方法设计的无乘法IIR数字滤波器的幅频响应
4 结语
本文提出了一种基于随机结构的无乘法IIR数字滤波器设计方法。此方法首先从结构上进行无乘法IIR数字滤波器的设计,然后通过SPS-DE算法对结构进行优化,最后设计实验进行了有效性的验证。利用该方法设计的无乘法IIR数字滤波器能够满足结构要求,性能得到了提升。这种方法为无乘法IIR数字滤波器的设计拓展了一种新的思路。

