基于Nyström方法的偏好特征提取
杨美姣,刘惊雷
(烟台大学 计算机与控制工程学院,山东 烟台 264005)
0 引言
近几年,核方法已经成功地应用于各种现实世界中,尤其是那些具有高度复杂性和非线性结构的问题中。核方法已经被广泛地应用于各种机器问题,如分类、聚类和回归学习中。在基于核的学习中,输入的数据点被映射到高维的特征空间中,并将内部成对的数据存储在一个对称的半正定核矩阵中。核矩阵的核心作用是描述样本数据之间的相似性,目前在流形学习和降维中被广泛应用[1]。在实际应用中矩阵的规模往往较大,因此需要降低矩阵的规模,即对矩阵进行采样,将高维矩阵映射到一个低维子空间中,然后对低维空间中的矩阵进行分解,这样做不仅能减小矩阵的规模,解决矩阵溢出的问题,而且还能提高运算的效率。低秩矩阵分解和核学习是构建高级学习系统的两种有效的方法[2],这两种方法都可以降低大规模矩阵的计算成本。
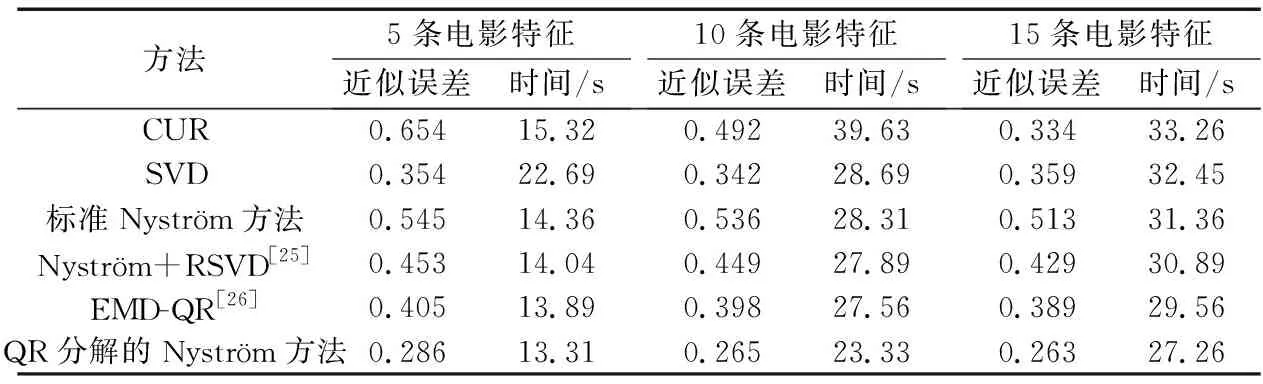
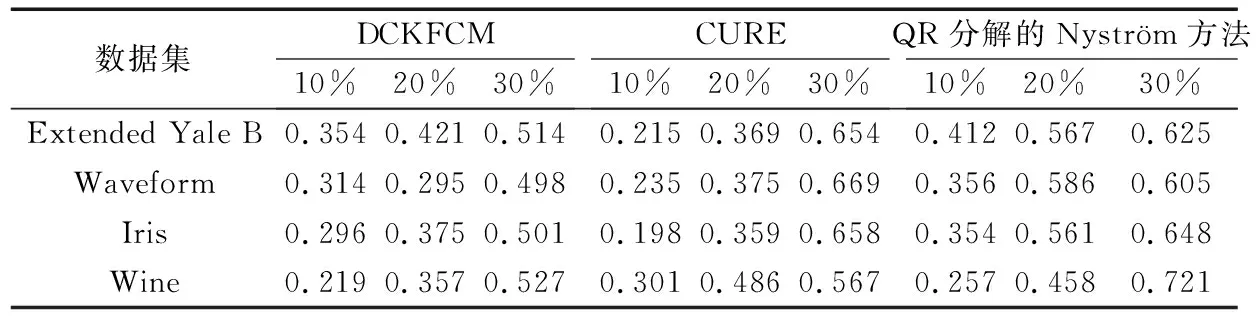
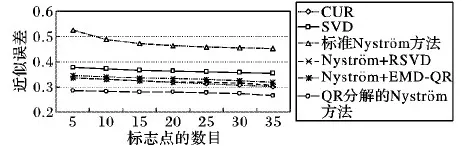
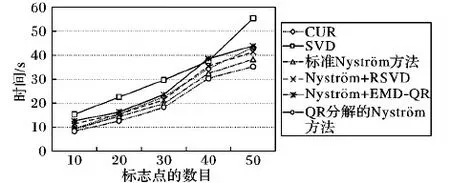
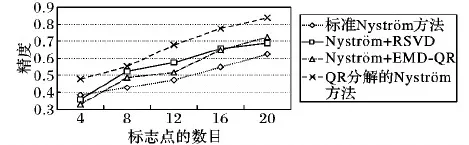
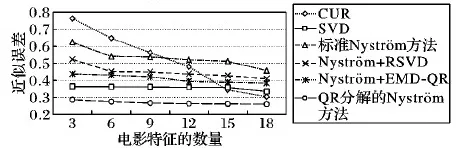
给定一系列n个点, 假设核矩阵K的大小为n×n。核矩阵K≈LLT,其中矩阵L∈n×k,秩k Nyström方法的原理是选择一组“地标点”(有标志性的点),然后计算输入数据点和标志点的内核相似矩阵[5]。Nyström方法的衡量标准与标志点的选取密切相关,若选取的标志点具有普遍代表性,则其相似性越高。原始的Nyström方法是从输入的数据点中随机地选择标志点[6],随机采样有很多不确定性,使得原始Nyström方法的精度并不是很高。本文中将Nyström方法与QR方法相结合,即将Nyström方法的内部矩阵C进行QR分解,将分解后得到矩阵Q和R,利用分解后的矩阵R和Nyström方法的内部矩阵W+相乘,得到矩阵RW+RT,随后对矩阵RW+RT进行特征分解,得到矩阵V′、Σ′和V′T3个矩阵,最后得到最佳的Nyström近似。 本文主要工作如下: 1)标志点的选取影响着对偏好特征的选择。为了提高采样后的Nyström方法的精确度,利用自适应的采样方法,即通过多次遍历并及时更新抽样概率,选取有代表性的标志点,随着遍历次数的增加,采样后的误差会大大减小。与传统的随机抽样相比,自适应采样的精度会明显提高,同时也避免了随机抽样中标志点选取的偶然性。要保证选取的标志点尽可能包含项目的特征,本文设计了标志点选取的算法,该算法跟传统的算法相比,精度有了一定的提高。 2)本文中将标准的Nyström方法与QR分解相结合,解决了标准Nyström方法中内部矩阵受到秩限制的问题。本文中的算法还可以用来描述当标志点的数目超过目标秩k时的最佳k近似,因此,本文提出的算法可以与任意标志点选择方法相结合来寻求最佳k近似。 3)在真实的观众对电影评分的数据集上进行了测试,该电影数据集中包含480 189个用户,17 770部电影,根据观众对电影的评分结果进行偏好特征的提取,并与其他算法如奇异值分解(Singular Value Decomposition, SVD)、行列组合(Column Union Row, CUR)、标准的Nyström方法、Nyström方法和正则奇异化分解(Regularized Singular Value Decomposition, RSVD)的组合(Nyström+RSVD)以及基于范例的低秩稀疏矩阵分解(Exemplar-based low rank sparse Matrix Decomposition, EMD)和QR分解的组合(EMD-QR)方法进行了比较,并选取了凸数据集和非凸数据集进行了实验,从理论和实验两个方面证明了本文所提出的算法的有效性。 本章主要介绍了一些相关的定义和符号,为后面工作中要用到的定义和概念作了相应的描述。 假设矩阵A=[a1,a2,…,an]∈Rm×n是一个n中包含n个数据点的列矩阵。计算特征空间中的内积用到“核函数”,它在原始空间上定义为:Bij=b(ai,aj)=〈Φ(ai),Φ(aj)〉,∀i,j=1,2,…,n,其中,Φ:a|→Φ(a)是内核诱导的特征图。n个映射数据点的所有成对内积存储在核矩阵K∈Rn×n中,第(i,j)个条目是k(i;j)。高斯和多项式核矩阵是对称半正定核矩阵的两个众所周知的例子[7]。尽管在数据的非线性表示中内核很简单,但是大规模数据集的内核矩阵的计算和存储却很棘手[8]。核矩阵的内存为O(n2),内存和计算成本都是以数据点数量的平方为尺度,而且在后续的学习过程中,核矩阵在计算上也需要花费很大的成本。例如,核主成分分析(Kernel Principal Component Analysis, KPCA)算法需要计算核矩阵的特征值分解[9],标准的算法需要的时间复杂度为O(n3),且需要多次遍历矩阵K。在其他的基于核的学习方法如核岭回归中,计算的时间复杂度为O(n3)。对于规模较大的矩阵,要充分考虑计算计算的时间复杂度。 对于任意一个矩阵A∈m×n,A(j)(j=1,2,…,n)定义为A的第j列向量,相应的A(i)(i=1,2,…,m)定义为A的第i行向量。可以将矩阵A分解为: A=UΛV′ (1) Nyström方法首次被提出是用于解决近似积分特征函数的问题,后来被用来处理低阶近似的核心矩阵[12]。假设给定一个核函数k(·,·)以及具有底层分布的样本集p(·),Nyström方法旨在解决以下积分: (3) 其中:φi(x)、λi分别是第i个特征值函数和关于p的k(·,·)算子的特征值[13]。假设输入一个对称的半正定核矩阵K∈n×n。若矩阵的秩rank(K)=r≤n,即存在一个L∈n×n,使得K=LTL。Nyström方法的对象是对称的半正定矩阵,要使用Nyström方法,必须对原始的矩阵进行预处理,将矩阵转化为对称的半正定矩阵。本文中,利用采样方法采取其中的c≪n列来产生矩阵B的近似矩阵假设采样的列数c已给定,重点是用自适应方法选出其中的列。矩阵C表示由这些列组成的大小为n×c的矩阵,矩阵W是一个大小为c×c的矩阵,由这些相互正交的列与矩阵B相对应的行组成。矩阵B是对称半正定矩阵[12],因此,矩阵W也是对称半正定矩阵。一般的,矩阵B的行和列可以根据采样后的结果重新排列,可以将矩阵B和C表示为: (4) (5) 其中:矩阵W是一个大小为c×c的矩阵,矩阵B21的大小为(n-c)×c,矩阵B22是一个大小为(n-c)×(n-c)的矩阵。 (6) Nyström方法可以近似为矩阵K的前k个特征值(Σk)和特征向量(Uk)。 (7) 该近似将矩阵K的3个模块重新组合,B22是矩阵K中W的Schur补。 (8) 矩阵W的SVD的时间复杂度是O(kc2),矩阵乘C的时间复杂度是O(kcn),因此整个Nyström近似的时间复杂度为O(kcn)。式(6)又可以表示为: (9) 其中: (10) Nyström方法构造矩阵Lnys的时间复杂度是O(pnc+c2k+nck),其中构造矩阵C和W的时间复杂度是O(pnc)。执行矩阵W的部分特征值分解的时间复杂度为O(c2k),而矩阵乘法CVk的时间复杂度为O(nck)。因此,对于k 与标准的Nyström方法不同,自适应的Nyström是在标准Nyström方法上作的进一步改进,即每次采样后,都将剩余列的概率按照降序排列,取其概率较大的列,能尽可能地表示原始矩阵,改进后的Nyström方法能够与任意标志点选取方法相结合,寻求给定秩数的最佳近似[14]。 Zhang等[20]提出了一种使用k均值聚类产生质心的信息列的算法,该算法已被证明具有良好的精度,这种算法的原理是使用样本外扩展来生成矩阵B的c个有代表性的列。经过对k均值聚类产生质心的信息列的算法的改进,提出了一种具有较强理论基础(自适应)的抽样算法,该方法要求在每次迭代中遍历矩阵B,这样可以提高采样的精度。 定理1 自适应采样。假设给定任意一个矩阵A∈m×n,从其中选取一系列的列向量来构造矩阵S,则每次采样都遵循以下分布,第i列被选择的概率可以表示为: (11) 其中:A(i)来表示矩阵A的第i列。 根据定理1可以设计一个高效的采样算法,但是该算法有一个特点,首先要对原始矩阵进行遍历,得到其原始分布概率,然后根据得到的各列的概率进行采样。 随着采样次数的增加,误差会随着遍历次数的增加而减少,因此,多次遍历对于稀疏矩阵的近似非常重要。 定理2 自适应采样的数学描述。假设S=S1∪S2∪…∪St表示对矩阵A的列进行采样后的结果,对于j=1,2,…,t,集合Sj表示的是对矩阵A的s列进行采样后的结果。第i列被选择的概率可以表示为: (12) 其中:E1=A,E1=A-πS1∪S2∪…∪Sj-1(A),其中πS(A)表示的是A在S的生成空间上的投影。 自适应采样方法对稀疏矩阵较为重要,当采样的矩阵较为稀疏时,尤其是像观众对电影评分这样的大规模的稀疏数据,采用这种方法可以降低计算的复杂度,提高运算效率。 与固定采样不同,自适应采样在每次选择完一组样本后,都会更新所有样本的概率[21],最终产生最佳的k秩近似。其基本思想是从列的初始分布开始,从矩阵B中选择s 对于一个大小为n且标志点数目为c的数据集而言,矩阵C∈n×c和矩阵W∈c×c被重新构造,形成低秩近似矩阵n×n。虽然最终的目标是找到一个秩数不超过k的近似值,但是通常要选择c>k个有标志性的点,然后限制所得到的近似秩最大值为k[24],这样做的好处是可以使得近似的精度较高。例如,近似误差是通过c个有标志性的点引起的总的量化误差函数。很显然,标志点选取的数目越多,总的量化误差就会越小,这样就可以提高k秩近似的质量。因此,选取一种有效而精确的方法对矩阵来讲是非常重要的。 (13) 其中:第2个等号中是将矩阵C∈n×c进行了QR分解,即C=QR,其中矩阵Q∈n×c,R∈c×c;而第3个等式中是对矩阵RW+RT进行特征值分解,即RW+RT=V′Σ′V′T,其中,对角矩阵Σ′∈c×c包含主对角线上按照降序分布的c个特征值,V′∈c×c则是相应的特征向量。QV′∈c×c都是正交的,因为Q和V′都有正交的列: (QV′)T(QV′)=V′T(QTQ)V′=V′TV′ (14) 为了产生标志性的点,首先要产生一个信号矩阵H∈n×n,即两者出现的概率相同,均为0.5。通过计算矩阵HB来找到其低维框架标准的矩阵的乘法时间复杂度为O(n3)。矩阵的乘法可以并行执行,这样都可以显著加速。然后,对投影后的低维矩阵进行k-means聚类,将数据集进行分割: (15) 具体的算法如下: 算法1 基于Nyström方法的聚类。 输入:用户-电影的评分矩阵A∈Rm×n,标志点的数目c; 1) 调用算法2得到相似矩阵B; 2) 调用算法3得到采样后的矩阵C; 3) 调用算法4得到主要的特征值和特征向量; 4) 产生一个随机符号矩阵H; 5) 6) 利用式(15)计算原始空间中的样本均值; 7) Z=[z1,z2,…,zm]∈p×c; 8) 返回:C∈Rm×c。 算法2 求相似矩阵B。 输入:用户-电影的评分矩阵A; 1) 输入用户-电影数据集A; 2) returnB; 其中,X=x1,x2,…,xn∈Rn,表示的是观众对电影感兴趣的属性个数,样本的协方差矩阵为M。根据距离公式,可以将观众对电影的评分矩阵转化为用户(电影)与用户(电影)的相似度矩阵,即对称的半正定矩阵。 算法3 基于自适应Nyström采样方法。 输入:用户-用户的相似度矩阵B,采样的列数c,每次遍历的列数s; 输出:采样后的矩阵C。 步骤1 初始化抽样点的索引的集合B; 步骤2 对于i∈[1,2,…,t],repeat: 1)Pi← ADAPTIVE-SAMPLING(S); 2)根据pi选取的索引构造Bi; 3)将得到的B∪Bi重新赋值给B; ADAPTIVE-SAMPLING(S); ①选出与B中相对应的矩阵的列,构造矩阵C; ②计算矩阵C的左奇异向量UC; ④每个j∈[1,2,…,c]; repeat:1)若j∈S,则pj=0; 步骤3 更新抽样点的抽样概率p/‖p‖2; return 概率集合p和采样后的矩阵C; 算法4 通过QR分解的Nyström。 输入:采样后的矩阵C,核函数f,目标秩k; 1) 对矩阵C执行QR分解:C=QR; 2) 计算特征值分解:RW+RT=V′Σ′V′T; 3) (16) 特征点Z∈p×c的整个估计核矩阵的k个主要的特征值和特征向量的时间复杂度为O(pnc+nc2+nck),其中O(pnc)表示组成矩阵C和W的时间复杂度,而QR分解的时间复杂度是O(nc2),计算RW+RT的时间复杂度是O(n3),计算矩阵乘法的时间复杂度则是O(nck)。 举个简单的例子,如核矩阵是一个3×3的矩阵: 假设对核矩阵进行均匀采样,采样的列为c=2,假设采样的列为第1列和第3列,即: 在标准的Nyström方法中,首先要计算的是内部矩阵W的最佳近似。根据标准的Nyström方法的计算公式,可以得到: 可以计算矩阵C的QR分解,即C=QR 计算RW+RT并得到其特征值和特征向量,即RW+RT=V′Σ′V′T: 对于相同的秩,Nyström与QR分解相结合得到的最佳近似矩阵的精度较高。 本文采用的是改进的Nyström方法,即对Nyström中的矩阵C进行QR分解,得到矩阵Q和R,然后利用得到的R以及Nyström方法中的内部矩阵W+,得到矩阵RW+RT,并对其进行奇异值分解,利用矩阵V′、Σ′和V′T3个矩阵,最后根据式(13)得到最佳的Nyström近似。这样做的好处是: 1)算法的时间复杂度降低。首先将观众对电影的评分矩阵运用马氏距离转化为观众与观众或者电影与电影之间的相似度矩阵,然后利用Nyström方法的特性,即Nyström的对象是对称的半正定矩阵,对相似度矩阵B进行自适应采样,相对于原始的观众对电影的评分矩阵来说,从规模上大大地减小了,因此,该方法从计算效率上来说,有了较明显的改善。 2)算法的空间复杂度降低。本文是对矩阵B进行了自适应采样,由于Nyström方法的特性,只需要对其中的列进行采样即可,相对于CUR中需要同时采样数据的行和列,本文所提出的算法的计算复杂度降低了,同时也将原始的高维数据降低到一个低维的子空间中,因此,在一定程度上也解决了大规模矩阵溢出的问题。 3)精度提高。相对于标准的Nyström方法,改进后的算法对矩阵C进行了QR分解,利用矩阵R以及矩阵W的伪逆,得到一个新的矩阵RW+RT,并对其进行SVD,相对于直接对观众对电影的评分矩阵进行SVD,采样后的矩阵更能表示观众或电影的特征,因此,经过改进的Nyström方法的精度有了较大的提高。 定理1 算法的时间复杂度。算法时间复杂度为:O(nc2),其中k为矩阵的秩,c表示的是采样的列数,n表示原始大矩阵的规模。 证明 改进后的Nyström方法与QR相结合的时间消耗主要有几个方面:第一个是自适应采样的时间复杂度O(nc2+Mc),其中,M表示相似矩阵B的中非零点的数目,k为矩阵的秩,c则表示的是采样的列。另一个是形成矩阵W和C的时间复杂度O(nc2),RW+RT特征值分解的时间复杂度为O(c3),QR分解的时间复杂度为O(nc2),核矩阵的k个主要的特征值和特征向量的时间复杂度为O(pnc+nc2+nck),最后是计算矩阵QV′的时间复杂度O(nck),但是由于n≫c>k,因此,总的时间复杂度为O(nc2)。 本文采用真实的观众对电影的评分数据集进行测试,并将本文所提出的算法与已有的偏好特征提取算法(SVD、CUR、标准的Nyström方法、Nyström+RSVD、EMD-QR)进行对比。 本文中的所有实验都是在一台8 GB DDR3内存和主频为2.8 GHz的Intel Pentium CPU的计算机上进行的,计算机的系统为Windows7 64 b,所有的实验所用的软件为Matlab 7.0。由于实验中可能存在一些不确定因素,因此,每次实验都做了6次,取其平均值作为最后的结果。 该实验中所采用的数据集是由著名的电影公司Netflix提供的数据集,该数据集中共包括480 189个用户,17 770部电影总计100 480 507条评分记录。观众对电影的评分的有限性,导致数据集的稀疏性,且观众的类型也相对较多,对不同电影的评分也各不相同,导致该数据集的规模相对较大,对该数据集进行分析,运用传统的特征提取方法效率较低,运用本文提出的改进的Nyström方法,对其进行偏好特征的提取。 为了说明本文提出的改进的Nyström方法的优势,将其与已有的算法进行了比较。 1)CUR:CUR也是一种提取偏好特征的方法,但是相对于Nyström方法来说,需要对矩阵的行和列采样得到矩阵C,计算的复杂性会较高。由于Nyström方法的特殊性,只需要对矩阵的行或列采样即可得到矩阵C,因此,相对来说,计算的复杂度也会相应降低,占用的空间相对较小。 2)SVD:SVD是一种普遍的矩阵分解技术,对于特征提取来说,SVD是一种有效的方法,它能够将高维的数据降低到一个低维的子空间中,从而能降低对矩阵分析的复杂性,但是对于观众对电影评分这样的高维稀疏矩阵来说,并不推荐SVD。 3)标准的Nyström方法:由于受到内部矩阵秩的影响,导致整体的秩会受到限制。改进的Nyström方法是在标准的Nyström方法上作了修改,在标准的Nyström方法上将矩阵的内部矩阵进行QR分解,利用分解后的矩阵重新构造最佳的Nyström近似。 4)Nyström+RSVD:RSVD是SVD的一种推广。在求解稀疏SVD的过程中需要进行多次迭代,因此,算法的时间复杂度相对较高,与Nyström相结合后,虽然能够降低矩阵分解的复杂性,但是对于大规模的矩阵来说,并不推荐此方法。 5)EMD-QR:EMD算法首先要计算一个有代表性的数据子空间和一个近乎最优的降序排序近似,然后通过获得集群质心和指标进行矩阵分解。EMD-QR在采样时需要选择行和列,因此,对于大规模的矩阵来说,计算的时间复杂度也会有所增加。 本文中首先将用户对电影的评分矩阵转化用户与用户的相似度矩阵,用自适应采样方法得到C,然后对矩阵C进行QR分解,得到Q和R两个矩阵,然后利用矩阵R和W重新构造矩阵,并对构造后的矩阵进行SVD分解,得到V′、Σ′和V′T3个矩阵,然后利用得到的矩阵Q、V′和Σ′重新构造最佳的Nyström近似。矩阵恢复的能力越好,则说明该方法的精度越好。 从表1中可以看出,在同等条件下,即电影特征数量相同的条件下,可以看出与CUR、SVD、Nyström+RSVD、Nyström+EMD-QR以及标准的Nyström方法相比较,本文提出的与QR分解相结合的Nyström方法的近似误差更小,所用时间也较小。RSVD算法中,需要进行多次迭代,时间复杂度会较高[25]。EMD-QR算法中需要对行和列进行采样[26]。本文提出的方法是在标准Nyström方法的基础上进行的改进,与标准Nyström方法不同的是,该方法是将Nyström方法的内部矩阵C进行QR分解,得到Q和R两个矩阵,然后将矩阵R和标准Nyström方法中的矩阵W+相结合,得到重新组合后的矩阵RW+RT,并对其进行分解。因此,与标准的Nyström方法相比较,得到最佳近似矩阵,矩阵的规模相对较少,用到的时间就会相应减少,采样用到的方法是自适应采样方法,因此近似误差也会相应地减小。与CUR方法相比较,CUR中的采样方法用到的是统计影响力的方法,但是需要对矩阵的行和列同时进行采样,与Nyström方法的只需要对矩阵的列进行采样而言,用到的时间也会相应减少。对于SVD,直接对原始的观众对电影的评分矩阵进行SVD,由于原始的观众对电影的评分矩阵较为稀疏,得到的偏好特征的误差也会较大,且由于原始矩阵规模较大,因此,用到的时间也会有所增加。Nyström+RSVD方法由于受到矩阵规模的影响,时间复杂度会较大,而Nyström+EMD-QR方法需要对行和列进行采集,因此,对于大规模的矩阵也不推荐此方法。 表2中描述的是在不同的数据集上不同算法的精度,对于采取不同比例的样本,各种方法上的精度各不相同。DCKFCM算法是在KFCM算法的基础上进行的改进,k-means算法对于非凸数据集很实用[27],但是对于非凸的数据集,如表2中的数据集,就不能采用k-means算法,因此,对其进行了改进,得到DCKFCM算法。CURE算法虽然对传统的方法进行了改进,但是由于这种方法采用的是随机抽样算法,因此,采样的精度并不会很高,也会影响最后的结果。表2中的数据是非凸数据集,有些算法对数据有要求,即只针对凸数据集,因此本文中用非凸数据集进行了比较。综合表1和表2,本文中提出的算法既适用于凸数据集,同样也适用于非凸数据集。 图1中描述的是标志点数目对不同方法的近似误差的影响,可以看出,标志点的数目越多时,近似误差也会随之减小。由于采样后矩阵的规模会相应减小,当采样的数目较少时,可能会失去原有矩阵的特性,导致近似误差较高,因为观众对电影评分的稀疏性,当标志点的数目较少时,可能会出现偶然性,但是对着标志点数目的增加,采样后的矩阵与原始矩阵的差距会进一步减小,因此,随着标志点数目的增加,近似误差也会相应地减小。影响观众对电影评分的因素有很多,但是只有前k个特征对其影响较大,基本上可以代表用户的特性,因此,当标志点的数目继续增加时,对其近似误差的影响也很小。 表1 各种方法的近似误差和运行时间 表2 不同算法在不同数据集不同比例样本时的精度对比 图1 各种算法与通过QR分解的Nyström方法的比较 图2表示的是各个标志点中不同方法的时间比较图,当选取的标志点的数目增加时,所用的时间也会增加。在一定范围内,随着标志点数目的增加,精度也会随之提高,但是由于采样方法的不同,获取相同数目的标志点所用的时间也不同:CUR中用到的是基于统计影响力的采样,需要对矩阵的行和列同时进行采样,与Nyström只需要对其中的行和列进行采样相比,时间自然会增加;SVD是直接对原始矩阵进行分解,因此,所用的时间最多;EMD-QR与Nyström相结合,虽然在一定程度上时间会相应的减少,但是EMD-QR也需要对行和列进行采样,因此,所用的时间也比本文提出的方法多。 图2 各种算法的时间比较 图3表示的则是各种Nyström方法和本文中提出的与QR相结合的Nyström方法,当选取的标志点的数目相同时,各方法的精度也会有所不同,这是因为不同方法得到的标志点的过程不同,得到的标志点的代表性也会有所差异,当得到的标志点具有普遍代表性时,精度就会高。标准Nyström虽然提供了一种求解近似的方法,但是由于受到内部矩阵的局限性,使其得到的最佳k秩近似不具有普遍性,只能得到与特定标志点选取的方法相结合,但是改进后的Nyström方法可以与任意标志点选取的方法相结合,本文采用的自适应采样方法,即每次采样后都要对概率进行重新排布,可以有效地提高采样的精度,得到的标志点普遍性更高,精确度更高。 从图4中可以看出,当电影的特征数目相同时,相对于其他方法,本文提出的通过QR分解的Nyström方法的近似误差较小,且随着所提取的电影数量的增加,近似误差会越来越小。本文的目的就是对电影的偏好特征进行提取,因此,在影响观众对电影评分的前k个主要特征中,所提取的电影的特征越多,近似误差就会越小。传统的CUR方法采用的是基于统计影响力的采样方法,即每一列所占的比重大小,虽然经过采样后,矩阵的规模会较少,计算的时间复杂度也会相应减小,但是采样方法的局限性,使得采样后的矩阵不能保证其原始用户的特征,即若某列中用户看过的电影数量较少,但每次的评分却较高,亦或是观众只对其中的某一类电影感兴趣,对其评分就会普遍偏高,以及某列中虽然观众看过的电影的数量相对较多,但每次的评分却相对较小,采用统计影响力的结果是前者被选择的概率可能会大于后者,显然,这对于分析电影的特征是不利的,前者观众可能关注的是某一类电影,而后者看的可能是多类型的电影,而这些电影却不是用户真正感兴趣的。而SVD中,则是直接对观众对电影的评分矩阵进行分解,得到的虽然是电影的特征,但由于原始矩阵的规模较大,这种方法也显然并不是最佳选择。标准的Nyström方法中,由于针对的是内部矩阵W+,要寻求其最佳k秩近似,因此就对矩阵进行了限制。将Nyström与RSVD相结合,虽然采样后的矩阵规模减小了,但是由于矩阵的稀疏性以及观众对电影评分带有主观性的特点,影响了该方法的使用。EMD-QR方法是针对低秩矩阵而言的,从中受到启发,Nyström采样的矩阵即为低秩矩阵,将Nyström与QR方法相结合,不仅能从时间复杂度上进行改进,精度也不会受到损害。 图3 各种Nyström方法的精度的比较 图4 不同电影特征下的近似误差 本文中描述了基于Nyström方法的偏好特征的提取,与传统的Nyström方法不同,本文在标准的Nyström方法上作了进一步的改进,不再受内部矩阵的限制,使得Nyström方法能与任意标志点选择方法相结合来寻求最佳k近似。这一点对于规模较大的稀疏矩阵来说尤为重要,选取一定的标志点能够减小矩阵的规模,本文中采用的是自适应的Nyström方法,在算法3中描述了该方法,与传统的采样方法相比较,该方法的精度要高于传统的方法。算法4中进一步说明了经过QR分解的Nyström近似,进一步得到其特征的特征向量。用Nyström近似后能尽可能保留近似前的矩阵的特性,因此对于精度和效率都有一定的改进。 未来工作包括:1)根据得到的用户和电影的特征,对用户感兴趣的电影进行推荐。2)本文中主要是对电影数据集进行的测试,在未来的工作中会对更多的不同的数据集进行测试,进一步验证特征提取的有效性。1 相关工作
1.1 核矩阵
1.2 奇异值分解
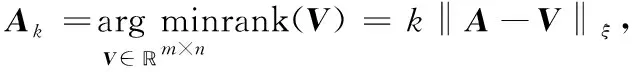
1.3 低秩矩阵近似
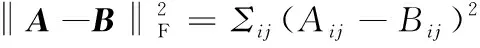
1.4 Nyström方法
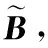

2 自适应Nyström方法
2.1 自适应采样
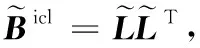
2.2 自适应Nyström采样
2.3 改进的通过QR分解的Nyström方法
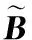
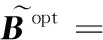
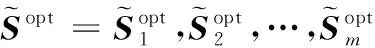
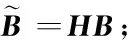

3 算法求解实例

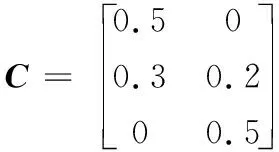

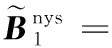

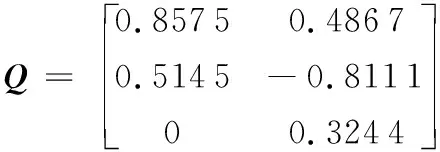
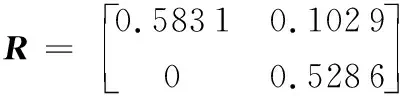
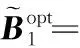

4 算法的评价
4.1 算法的优越性
4.2 算法的时间复杂度分析
5 实验环境、结果与分析
5.1 实验环境
5.2 实验中所用的数据集
5.3 实验设置
5.4 实验过程
6 结语

