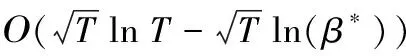快速在线分布式对偶平均优化算法

李德权，王俊雅，马 驰，周跃进

(安徽理工大学 数学与大数据学院，安徽 淮南 232000)(*通信作者电子邮箱784836893@qq.com)

0 引言

近年来, 网络和分布式计算的迅猛发展造就了从大型集成电路计算机到分布式网络工作站的一个跃变，这使得分布式网络受到了越来越多的重视，并在传感器网络、机器学习和智能电网等多个方面具有广泛的应用前景[1-3]。分布式网络中的个体通过相互协调合作, 可以有效解决各种大规模复杂现实问题，提高数据传递效率，增强网络鲁棒性。文献[4]基于分布式随机梯度下降算法建立模型，不仅更好地利用了全局数据信息，而且提高了分布式随机梯度下降算法的收敛速度和性能。文献[5]提出了基于Push-sum的分布式对偶平均算法解决优化问题，但并不能实时处理网络数据流，造成网络中时间和资源浪费，成本代价高。因为在实际应用中，分布式网络一般都运行在动态环境下，如可再生能源系统的调度和传感器观测是时变的，其不确定性对整个网络的成本函数造成重大影响，导致建立的优化问题更加复杂。为了解决这一问题，本文研究基于在线的分布式优化算法，在线分布式优化算法不仅有效提高了算法的鲁棒性，且在机器学习和网络数据流实时处理方面有着重要应用[6-7]。作为衡量在线优化算法性能的一个重要指标，Regret界刻画了随时间推移的累积成本与最佳固定决策所产生的成本之间的差值，因此在线优化算法的优劣可由Regret界的大小进行判断。

在强连通网络环境下，本文基于在线分布式对偶平均(Online Distributed Dual Averaging， ODDA)算法以Regret界作为底层网络连通性的函数[8]，突出了网络拓扑与在线算法之间的联系，并广泛应用于高性能网络的在线设计、信号处理、分布式控制等方面[9-10]。为了实现分布式对偶平均，文献[5]要求网络中的节点基于Push-sum算法达成一致性，本质上是非线性算法，这就为求解带来了困难, 而ODDA采用的是线性一致性算法。然而，和常用的分布式次梯度算法相比，ODDA是典型的一阶分布式优化算法，收敛速度较慢，对于一般凸优化问题仅具有次线性收敛速率[11-12]。为了及时处理分析网络数据流，提高收敛速率，改进Regret界，本文将在线分布式对偶平均(ODDA)算法与添边方法相结合，对网络拓扑进行优化设计以实现算法更快的收敛速度，设计了一种改进的快速一阶分布式在线对偶平均优化(Fast first-order Online Distributed Dual Average optimization， FODD)算法，并对其性能进行了理论分析。

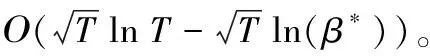
1 模型建立

1.1 图论

网络模型 个体或节点间的信息交换可建模成网络Gt(V,Et,Pt)，其中：V={1,2,…,n}表示个体集合，Et⊂V×V表示网络中所有边构成的集合，Pt表示Gt所对应的权重矩阵。l～(i,j)∈Et表示t时刻连接节点i和j的第l条边，Ni={j|(i,j)∈Et}∪{i}表示节点i在t时刻的邻居集合。若任意两个有序节点之间都存在一条路径，则称图Gt是连通的。本文假设Gt任意时刻都是连通的，且边有先后顺序。

权重矩阵Pt为网络拓扑图Gt所对应的权重矩阵，且若(i,j)∈Et，(Pt)ij>0，否则(Pt)ij=0。本文的权重矩阵是双随机对称矩阵，即满足：

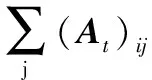
1.2 分布式在线优化模型

分布式在线优化算法中，t=0,1,…,T表示迭代次数，网络中的节点i∈V在每次迭代t时给出一个本地估计，记作xi(t)，进而对未知的本地凸损失函数ft,i(xi(t))进行观测。

本文考虑如下分布式凸优化问题：

(1)

s.t.x∈χ

其中:ft,i(xi):Rd→R是仅为节点i∈V所知道的局部凸损失函数，x=(x1,x2,…,xn)∈χ表示所有节点本地估计的集合，χ是一个凸紧集。

为了衡量分布式在线学习优化算法，对∀t=0,1,…,T通常用如下两类Regret界进行刻画。第一类是分布式在线Regret界：

(2)

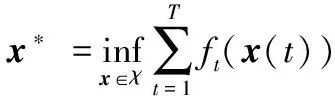
(3)

在线优化的目的是缩小Regret界，即随着时间推移，尽可能缩小累积成本与最佳固定决策所产生的成本之间的差额。当迭代次数T→∞，RT/T→0是次线性的，说明在线学习算法的解在渐近意义上收敛到全局网络最优解，即RT=Ο(T)。

2 问题描述

2.1 连通度不断增长的进化网络

文献[16-17]研究表明，ODDA的收敛速度与网络拓扑的代数连通性有关。由文献[17]的加边方法，本文通过对底层网络添边，建立连通度不断增长的进化网络模型。

Gt是随时间t单调递增、连通度不断增长的进化网络：

0<λn-1(L0)≤λn-1(L1)≤…≤λn-1(LT)

由Perron矩阵Pt可得：

σ2(P0)≥σ2(P1)≥…≥σ2(PT)

(4)

其中σ2(Pt)是Pt的第二大奇异值，Pt也可以表示为Gt图结构[16]：

(5)

其中：δmax是Gt的最大度，Pt是半正定的。

2.2 选边

由于代数连通度在边集中单调递增，通过添边可以获得连接良好的网络拓扑。本文选边方法是通过寻找拉普拉斯矩阵中零元素的位置，删除因自身和方向性导致多余的边来确定候选边集，然后选择任意两个未连接的节点进行添边。

对初始图G0添边得到图的拉普拉斯矩阵为：

(6)

其中：K=n(n-1)/2-m0表示可以添加到G0的候选边集数量，它是完全图边的数量n(n-1)/2和初始图G0边的数量m0的差；wl表示是否选择第l条候选边的布尔变量，如果选择候选边l，则wl=1，否则wl=0;al表示选边l所对应的边向量。

添边使网络具有更好的连通性，但容易消耗更多的网络资源。因此，进一步提出如下选边优化问题，达到网络连通性和资源消耗的最佳平衡：

(7)

s.t.w∈C1或w∈C2

其中：P(w)：=I-(1/n)L(w);C1={w|w∈[0,1]K}，当边数为k时，C2={w|w∈C1,1Tw=k};c=[c1,c2,…,cK]T，cl表示已知的第l条边成本；r>0表示衡量达到大的网络连通性和消耗小的网络资源的相关重要性的正则化参数。

2.3 添边

经过选边后，随时间t不断在网络上添加被选择的边，以生成代数连通度不断增长的进化网络，由此产生网络添边问题。为便于分析，假设随着时间增加每次网络最多只增加一条边[19-21]。则图的拉普拉斯矩阵的动力模型[17]为：

(8)

3 FODD算法

本章将文献[8]中的在线分布式对偶平均方法与文献[17]中提出的增加网络连通性的加边方法相结合，提出FODD算法来解决问题(1)中的优化问题。

3.1 FODD算法

算法1 FODD算法。

输入：节点数n(∀i∈V,V={1,2,…,n})，最大迭代次数T，参数{α(t)}；

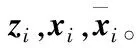
1)

生成初始图G

2)

根据选边优化的极小问题确定候选添边集w

3)

给出初值：xi(1)∈χ，zi(1)=0，∀i∈V

4)

计算次梯度gi(t)∈∂ft,i(xi(t))，∀i∈V

5)

fort=1:Tdo

6)

if |wt|>0

7)

根据候选边集wt，计算连通度增加最大的边lt

8)

9)

10)

wt+1=wt-lt

11)

end

12)

13)

14)

15)

end for

(9)

分别表示分布式在线对偶平均算法中对偶变量和次梯度的平均值。而

(10)

表示算法中的原始变量。

4 FODD算法的收敛性分析

本章将给出增长的代数连通度与Regret界之间的关系。为进一步分析，引进下面几个引理。

引理1[8]设网络中每个个体i的损失函数ft,i是L-lipschitz连续，即:

ft,i(x)-ft,i(y)≤L‖x-y‖2; ∀x,y∈χ

则对序列xi(t)和zi(t)，Regret界满足下面不等式：

(11)

引理2[17]对双随机时变矩阵φ(t,s)=PtPt-1×…×Ps(s≤t)，式(12)成立：

(12)

其中σ2(P)表示矩阵P的第二大奇异值。

此外，基于引理2，文献[17]研究表明：Regret界与矩阵φ(t,s)的谱密切相关且成立：

进一步地，对满足式(8)的动态网络有如下结论：

引理3[17]对∀i∈[n]，∀t=0,1,…,T，zi(0)=0，可得Regret界：

(13)

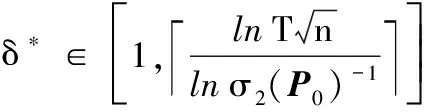
δ∈N+

其中：β是衡量σ2(Pt)和σ2(P0)比值的变量，而δ用来刻画所添的边与网络模型快速混合所消耗的时间。

基于引理1给出了Regret约束，为定理1的证明作了准备，可得到如下关于FODD算法Regret界的重要结论:

(14)

证明 由引理1和引理3得：

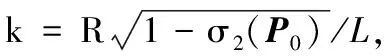
则对∀i∈[n]，下式成立：

定理2 在定理1的证明下，有以下等式成立：

(15)

证明 由ft(x(t))的凸性可知:

进而可得：

则对平均Regret界有：

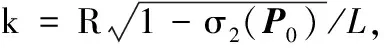
(16)

证明 由文献8的定理2可得静态网络的Regret界：

又根据文献16的定理2可知:

故可得静态网络情形下的Regret界收敛速度为：

(17)

证明 由定理1易证。

由推论1和推论2对比可知：式(17)的第二项刻画了不断增长的代数连通度。当β*=1时，在代数连通度不断增加的网络拓扑下的Regret界(17)变成了静态网络下的Regret界(16)；同时，当0<β*<1时，网络拓扑的代数连通度不断增长，此时Regret界(17)的上界比(16)更小，从而与分布式在线对偶平均算法相比，所提算法1在代数连通度不断增长的网络中计算更为精确。

5 数值实验

本章通过数值实验来验证FODD算法的性能，考虑具有5个节点的随机网络，任意连接2个未连接的节点，生成加边后的网络拓扑图，如图1。

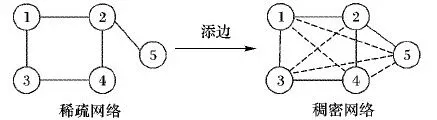
图1 加边后的网络拓扑图

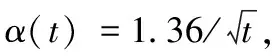
图2表示不使用加边方法时所有个体的状态轨迹图。在ODDA算法[8]的作用下，当迭代次数T到达200时，在误差允许的范围内，网络中所有个体的状态最终达成一致，其状态最优值在36的邻域内。图3表示通过图1所示的加边方法后所有个体的状态轨迹图。在本文FODD算法(即加边后的ODDA算法)的作用下，当迭代次数T仅达到50时，网络中所有个体的状态值已达成一致，其状态最优值也在36的邻域内。图2和图3对比表明：网络中所有个体状态都达到一致，但使用加边方法后，网络中个体的收敛速度更快，网络中占用的时间和资源更少，成本更低，验证了本文所提FODD算法(即加边后的ODDA算法)的收敛速度比ODDA算法更快。

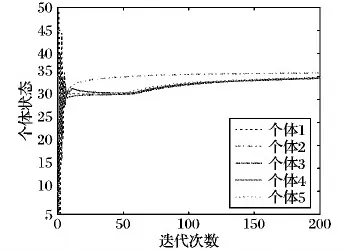
图2 ODDA所有个体状态轨迹

图3 FODD算法所有个体状态轨迹

图4表示ODDA算法与本文FODD算法作用下的平均损失性能对比，可以看出：本文FODD算法的全局目标函数的平均损失性能趋于零的速度，明显快于未加边的ODDA算法。即在相同网络环境下，使用加边方法可使整个网络以更快的收敛速率实现优化目标，解决优化问题。

图5表示ODDA算法与本文FODD算法作用下的平均差异性能对比，可以看出：不加边的ODDA在在线学习中保持着较高的一致性，而较高的一致性可能会远离真实值，产生较大的平均差异，而FODD算法的平均差异明显小于未加边的ODDA算法，一致性更趋于真实值。此外，当迭代次数T到达100时，FODD算法全局目标函数的平均差异已经趋近于零，明显快于未加边的ODDA算法平均差异的收敛速度。图4、5进一步表明：与ODDA算法相比，本文的FODD算法具有更好的收敛性能。

图4 平均损失性能对比

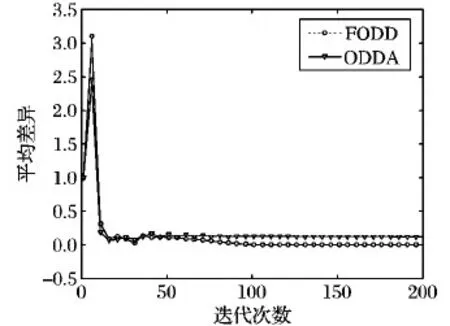
图5 平均差异性能对比

下面是Regret与平均Regret收敛速度在静态网络下和动态网络下的对比：

1)RT(x*,xi)：

静态网络拓扑收敛速度：

动态网络拓扑收敛速度：

静态网络拓扑收敛速度：

动态网络拓扑收敛速度：

可以看出动态网络情形下的Regret和平均Regret收敛速度明显快于静态网络情形下的Regret和平均Regret收敛速度。

6 结语