应急物资配送车辆调度模型与优化综述

曹 琦，曹 阳

(陆军勤务学院 勤务指挥系，重庆 401331)(*通信作者电子邮箱roy1976@163.com)

0 引言

当今世界一直遭受自然灾害的威胁，近年来，越来越多的重大灾害频频发生，如2008年汶川地震、2010年舟曲泥石流、2011年日本海啸、2015年尼泊尔地震，以及不久前在四川九寨沟和新疆精河县发生的地震，造成人民群众生命和财产的严重损害。灾害发生后，迫切需要及时、准确、有效地将救援物资配送到受灾点，尽可能降低生命和财产损失。在公路、铁路、海运、空运等多种运输方式中，公路运输具有机动灵活、周转速度快、适应性强等特点，是应急运输的主要手段，在抢险救灾过程中的地位是无可替代的。然而，绝大多数灾害的发生无法提前预知，救援时间十分有限，公路运输又存在车辆单位运输容量少、保障情形多变、受地理环境影响大等弱点。因此，利用数学建模方法和计算机仿真技术，辅助决策者在尽可能短的时间内拟定车辆调度方案具有重要的研究意义。

车辆调度问题(Vehicle Scheduling Problem，VSP)[1]是指以路程最短、费用最小或耗时最少等为优化目标，由车辆在一定的约束条件下从一个或多个配送中心向多个需求点配送货物，最终得到最优的调度方案。车辆调度问题是一个NP-Hard(Non-deterministic Polynomial-Hard)问题，通常受到时间性[2]、经济性[3]和安全性[4]等因素的影响，最后通过需求满足率[5]和公平性[6]等指标评定配送效果。在不同条件下，影响因素的重要性各不相同，评价指标所占权重也有差异，只有对真实情况作出合乎情理的假设，抓住问题的主要方面，对次要因素不予考虑，才能从技术上解决该问题。

在突发事件中，救援物资配送的车辆调度应着重考虑时间性因素，只有及时准确地把所需物资送到需求点，才能最大限度地减少损失。灾后一天甚至几个小时的救援时差就会关系到救援行动的成败，甚至关系到成千上万人的生命安全。另一个应重点考虑的因素是道路损毁的影响[7]，若损毁发生在灾害初期，需在等待抢修道路和绕道远行两者间进行抉择；若损毁发生在灾害发展的次生灾害中，这属于动态车辆调度问题，需对初始方案进行修正。如果存在多个需求点，应优先保障其中受灾最严重的区域，同时兼顾其他，这关系到物资配送的公平性，也是应急车辆调度的一个重要考虑因素。

近年来，国际社会对于应急车辆调度问题持续关注，并不断取得新的研究成果；国内则随着国家应急管理体系的建设，已将应急车辆救援问题提高到十分重要的地位。为此，本文专门分析了最近几年发表，模型构建和优化算法两方面分析过程都较为详实的30篇文献，提出了现有研究中存在的问题，研讨了未来发展趋势，以期了解该领域的最新研究进展，协助实际应用找到适合的研究方法。

1 应急物资配送车辆调度模型分析

本章着重从每个需求点是否仅被单车保障[8]、是否采用动态模型、数据类型、配送中心类型、有无时间窗、车辆类型、优化目标类型、周期类型等方面对物资配送车辆调度模型研究文献进行归纳总结，其中，数据类型是指物资配送的影响因素是确定的值或者是具有确信度的值(如需求量、道路通行速度、道路风险值等)[9-12]，周期类型是指救援物资是否分为多个时间段进行配送，结果如表1所示。下面按优化目标进行分类，对这些文献中构建的模型进行分析。

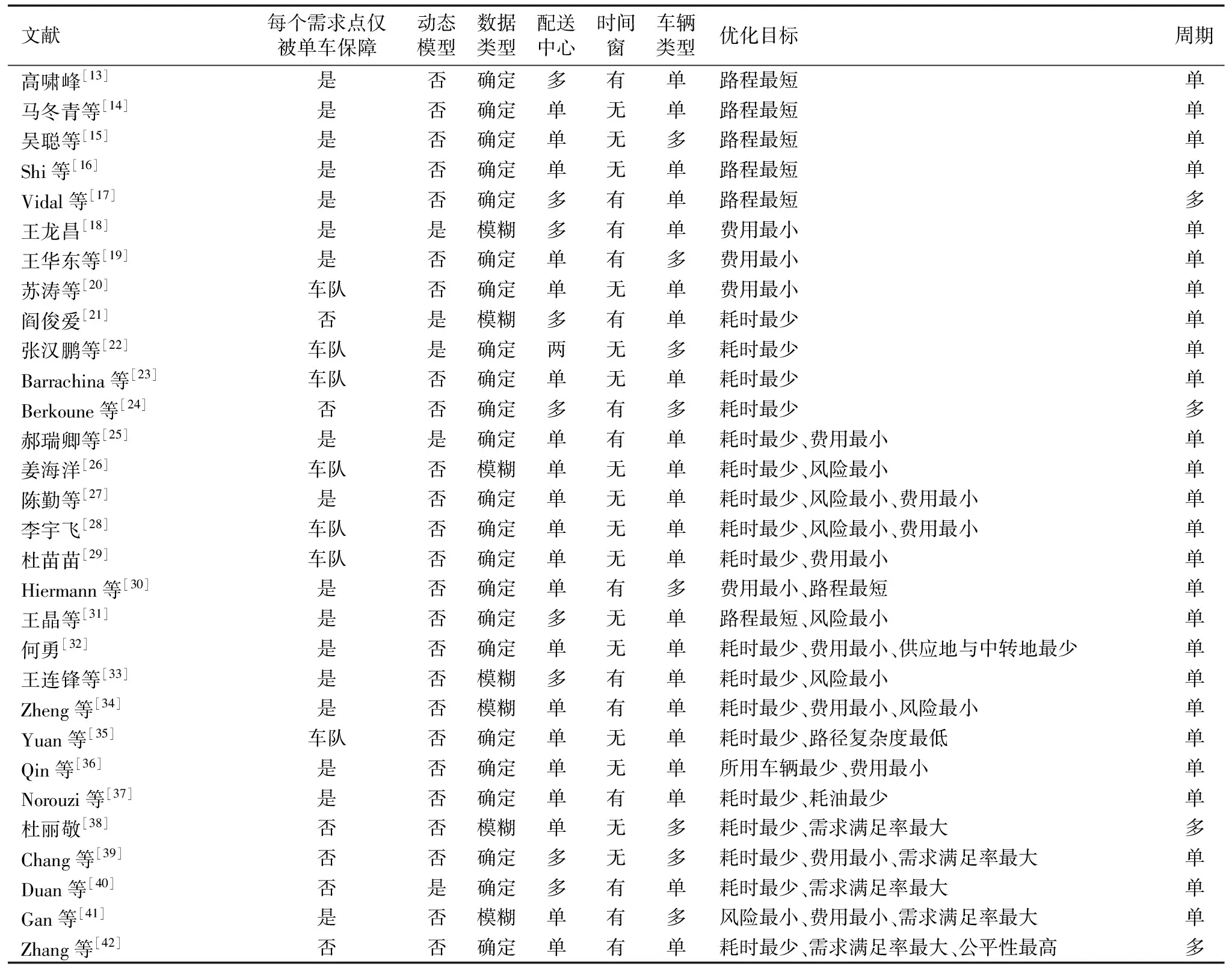
表1 物资配送车辆调度模型比较

1.1 单目标模型

1.1.1 路程最短

路程最短是指应急状态下，所有车辆行驶路径的总长度最短。高啸峰[13]建立了多个配送中心利用多辆车配送物资的模型，但未考虑动态模型问题。马冬青等[14]建立了单个配送中心对多个需求点进行配送的模型，并提出了双向配送的要求，有效提高了配送效率。吴聪等[15]也建立了单个配送中心对多个需求点进行配送的模型，其中着重考虑了多车辆类型的情况。Shi等[16]构建的模型只考虑了总距离最短一个目标，且每个需求点只能被单车服务。Vidal等[17]建立了多周期、多配送中心、需求点只能被特定车辆保障的三种带时间窗的车辆调度模型，综合考虑了物资配送过程中可能出现的情况。

1.1.2 费用最小

费用最小通常考虑每公里的行驶成本和车辆启用数，尽可能地减少运输费用。王龙昌[18]采用软硬时间窗相结合的方式构造惩罚函数，建立了多个配送中心利用多辆车进行配送的模型，并且伴随有新的配送需求产生。王华东等[19]在对配送成本的考虑中，加入了车辆数因素，并对配送时间加上了单向硬时间窗，该模型很好地解决了现代企业物流的许多问题。苏涛等[20]以总配送费用最小为目标，建立了单次配送中的路径规划模型，用于军事物流配送路径优化。

1.1.3 耗时最少

耗时最少是指整个配送任务的完成时间最短，它通常是应急车辆调度考虑的核心因素。阎俊爱等[21]通过对往期需求进行分析，模糊估计需求点所需的救援物资，采用实时信息/时变信息(实时信息是指当前时刻的道路信息，时变信息是指道路的历史数据)相结合的方式估计各路段的行驶速度，综合考虑时间窗和总配送时间最短，形成时间满意度最大这一优化目标。张汉鹏等[22]提出了二级配送的假设，区分主仓库、分发中心进行交替配送，该模型对主仓库发生灾害影响可能性的考虑具有启发性。Barrachina等[23]在综合考虑车道数和车辆密度的基础上建立模型，采用车载通信工具提前通知道路上的车辆，减少应急运输车辆的拥堵时间。Berkoune等[24]建立了多配送中心、多需求点的模型，考虑了最大工作时间，并且利用人在回路决策简化了算法，最终求得最少的总运输时间。

1.2 多目标模型

除了路程最短、费用最小、耗时最少外，一些文献把中转地最少、所用车辆最少、路径复杂度最低等影响因素也同时纳入了考虑范围，构成了多目标模型。在多目标处理中，大多数文献利用权重系数加权求和的方式，将多目标问题转化为单目标问题，这种方法简单易用，但求解效率不是太高，尤其是多目标间关联度较大的情况下，会造成解的质量不理想。部分文献选择直接求Pareto最优解，从而得到Pareto前沿(即Pareto最优解集)，解的质量可以得到较好保证，但求解的难度通常比较大。少数文献采取分层求解的方法[43]，即在满足第一优化目标的前提下，使第二优化目标尽可能最优，这种方法应用场景有其特殊性，普适性不强。

郝瑞卿等[25]在车辆速度一定的假设下，利用总配送时间与配送路程成比例的关系，把双目标问题转化成了单目标问题，建立了对应模型，并且考虑了动态模型问题，即在配送实施过程中，仍然会产生新的配送需求。姜海洋[26]考虑配送中的风险系数，建立了单个配送中心、多个需求点的模型，利用权重系数把最小化运输时间和最小化风险概率的双目标问题转化为了单目标问题。陈勤等[27]针对总用时最少、安全性指数最大、总配送费用最小建立了多目标模型，并且考虑了车辆的最大配送距离，但忽视了需求点的需求量和车辆运输容量的限制。李宇飞[28]考虑了受损道路的通行时间阻抗、基于道路可靠性的风险阻抗、基于时间依赖网络的费用阻抗，利用权重法计算综合边权，并进行无量纲化处理，形成单目标模型，对禁行路段和必经路段的情况也有所涉及。杜苗苗[29]考虑配送物资的种类、道路拥挤和驾驶员个人因素等情况，建立了物资分批运输模型，并利用权重系数转化为单目标问题。Hiermann等[30]建立了基于电动车进行物资配送的车辆调度模型，并综合考虑了电动车种类、电池消耗和充电站位置的影响。王晶等[31]基于车辆路线安排的总路程(费用)和车辆路线安排的风险两个目标建立了模型，并且在风险值中加入了运输量要素，使风险值更切合实际。何勇[32]建立了省级物资供应地、市级物资中转地、物资急需地三层配送模型，应用基于加权排序的方法将三个目标转换为单目标，解决了多源多汇的问题。王连锋等[33]建立模糊期望值模型，形成最小化车辆全部返回的期望时间和最大化最危险线路的期望安全通过率两个目标函数，并没有利用加权转化为单目标，而是直接求Pareto最优解。Zheng等[34]建立了铁路、空运、公路运输三种配送模型，并考虑通用车辆和专用车辆的情况，完成时间、总消耗、总风险三个优化目标的求解。Yuan等[35]建立了两种模型，第一种为每一路径上的运输速度是随时间连续变化的，第二种则是在紧急情况下，由于拥堵和恐慌发生，需尽量选择路径复杂度最小的路径。Qin等[36]考虑了车辆在体积和载重两个方面的约束，建立了单配送中心、多需求点的模型。Norouzi等[37]考虑了行驶速度的连续变化，把油料消耗列入优化目标，并在求解油料消耗时综合考虑载重量、风速、道路坡度、行驶距离等因素的影响。

1.3 考虑需求满足率、公平性的模型

在车辆向受灾需求点运输物资的过程中，提高需求点的总体需求满足率，并且兼顾救援的公平性是衡量一次救援行动是否成功的重要指标，在以下文献中得到了考虑。

杜丽敬[38]建立了多配送中心、多需求点模型，不要求每个需求点仅能被一辆车服务，考虑了多周期配送情况，并着重解决了对于需求满足率的要求，防止出现不公平配送的情况。Chang等[39]建立了多个配送中心向多个需求点进行配送的模型，并不要求每个需求点只能被一辆车服务，以需求的未满足率、交货时间和运输成本最小为优化目标。Duan等[40]建立了双层车辆调度模型，在已发生事故得到有效救援的前提下，尽可能地分配车辆以防范将来可能发生的事故。Gan等[41]采用效用界定救援物资对各个需求点的作用大小，进一步提高了物资配送的需求满足率。Zhang等[42]在模型构建中采取加权方法来折中三个目标，一要尽量减少未满足的需求量，即总需求和供应量的差额，二要试图获得最小的运输总时间，三要考虑救援行动的公平性，任何两个区域之间的令人满意的指数差异应该被最小化，同时还考虑了每天的最大工作时间，并且不要求每个需求点只能被一辆车服务。

1.4 存在问题

从以上文献分析中可以看出，目前应急物资配送车辆调度模型的研究存在以下问题：

1)多数文献仅仅考虑了每个需求点只能被单车保障的问题(或者简单抽象为车队进行保障)，但重大灾害后的救援物资需求量是巨大的，这与实际情况并不相符。

2)在考虑车辆调度的优化目标时，大多数文献以耗时最少、费用最小、路程最短或者风险最小为目标来研究配送问题，少数学者从需求满足率与公平性的角度来考虑救援物资的调度，对于物资损失和需求紧迫性的考虑不足。

3)对于动态问题的研究，大多数文献仅考虑需求的变化及道路的拥堵情况，忽略了道路损毁的动态变化，但在灾害发展进程中，道路极易被损毁，根据道路状况改进车辆调度方案是需着力解决的突出问题。

4)当配送车辆不足以一次配送到位时，多数学者是在全部车辆都完成配送的基础上，安排再次配送，并没有分别对每辆车安排多次配送任务，与实际配送情况不相符，配送方案缺乏灵活性。

5)几乎所有文献均认为车辆的初始状态是停靠在配送中心，而没有考虑车辆调配的情况，但我国大规模救援运输力量大多属于运输公司或救援部队[44-45]，配送中心本身运输力量往往不足以完成大规模救援物资的配送任务。

2 应急物资配送车辆调度模型优化分析

本章主要分析如表1所示的车辆调度模型所采用的优化方法，着重从优化目标数、优化方法、结果形式和有无对比实验等方面进行归纳总结，结果如表2所示。下面按优化方法进行分类，对这些文献中使用的优化算法进行分析。

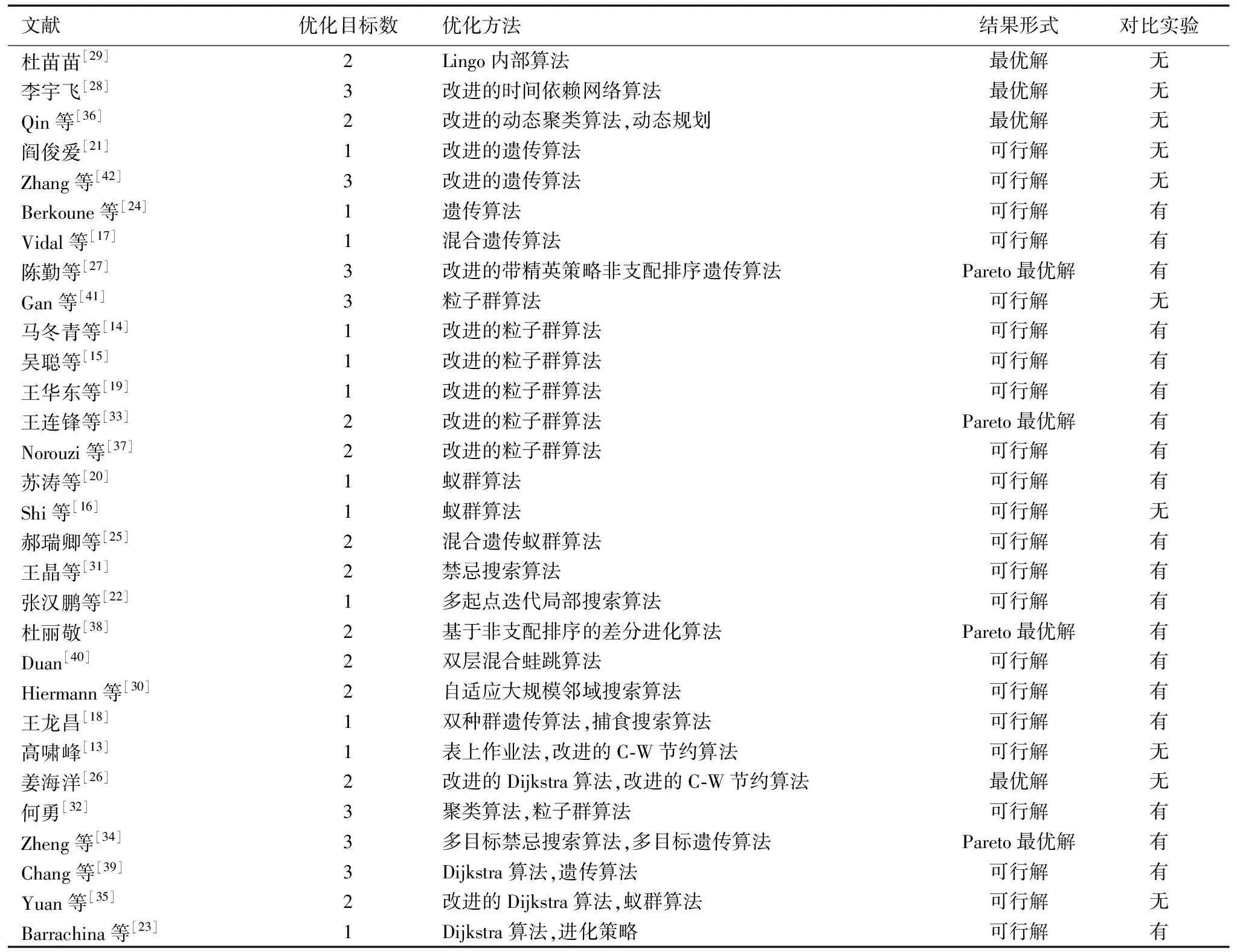
表2 物资配送车辆调度优化方法比较

2.1 精确算法

通过精确算法能够找到准确的最优解，在应急物资配送车辆调度问题中的常见精确算法有Dijkstra算法、分支-定界算法、时间依赖网络(Time Dependent Network，TDN)算法以及动态规划算法等，它们通常适合解决相对简单的优化问题。

杜苗苗[29]利用Lingo内部的精确算法求解最短路径，解决了单源单汇问题。李宇飞[28]提出考虑等待风险的时间依赖网络最短时算法和时间依赖网络综合最优算法，以求解军事物流配送的最优路径。Qin等[36]采用改进的动态聚类算法解决车辆分配问题，采用动态规划解决车辆路径问题，能够有效解决13个需求点规模的多车辆旅行者问题(Traveling Salesman Problem，TSP)。

2.2 启发式算法

随着问题规模的增大，精确算法难以求得最优解，从而促进了启发式算法的发展。应急物资配送车辆调度问题中被广泛应用的启发式算法主要包含遗传算法[46]、粒子群算法、蚁群算法[47]等。

2.2.1 遗传算法

阎俊爱等[21]采用变长度符号编码改进遗传算法，优化了初始种群选择和交叉变异过程，并在不同时刻进行了多次规划，解决了多源单汇问题。Zhang等[42]提出了亲密函数概念，以及对相关节点进行聚类的遗传算法。通过Courdeau-sdvrp数据集实例检测，能够解决实际配送问题。Berkoune等[24]提出了三种优化方法：一是使用Cplex12.1的经典分支绑定过程，具有启发式停止标准；二是快速构建启发式算法生成一组可行解；三是使用第二种方法输出的可行解作为初代的遗传算法。实验结果为：Cplex在问题规模过大时，无法得到有效解；集枚举启发式算法随着代数增加，运算效果会下降；遗传算法运算速度快，运算效果较好。在涉及3个配送中心和60个需求点的实例中，遗传算法在60 s的计算时间内产生平均差距小于0.72%的解方案。Vidal等[17]提出了具有适应性差异控制的混合遗传算法，采用多种算法分别针对三种车辆调度模型进行求解，具有适应性差异控制的混合遗传算法总能找到最优解，证明了有效性。陈勤等[27]采用改进的带精英策略非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ，NSGA-Ⅱ)进行单个配送中心、多辆车的路线规划问题求解，改进算法所得到的最优路径的总时间、总安全系数、总费用比NSGA-Ⅱ算法更优，但运行时间更长。

2.2.2 粒子群算法

Gan等[41]利用粒子群算法求解模糊数学模型，验证了该模型在应急救援中的有效性。马冬青等[14]对标准粒子群优化算法进行改进，在多次迭代中引入爬山操作，增强了算法的局部搜索能力。对爬山算法、粒子群算法、改进粒子群算法、动态规划法进行比较，在需求点数量较少时，爬山算法结果最优，在需求点数量较大时，改进粒子群算法最优。吴聪等[15]利用改进粒子群算法进行求解(使加速因子c1线性增大，c2线性变小)，并且选择标准粒子群算法、遗传算法、蚁群算法以及动态规划法与其进行200次迭代对比实验，改进粒子群算法找到最优解的成功率增加，而且求解时间也有所减少。王华东等[19]对标准粒子群算法的惯性权重w进行改进，提出一种惯性权值w非线性变化粒子群算法。采用标准粒子群算法、遗传算法、蚁群算法进行对比仿真实验，改进的粒子群算法的物流配送路径寻优成功率达98%以上。王连锋等[33]提出改进的约束多目标粒子群优化算法解决单配送中心问题，并引入局部搜索和变异算子避免算法早熟。在Solomon算例中，与NSGA-Ⅱ算法、带双存档机制的多目标粒子群算法进行比较，该算法可以在更短的时间内获得更高质量的解。Norouzi等[37]提出改进粒子群优化算法，使粒子的搜索速度随时间变化，优于经典粒子群算法，能提升6%的优化效果，节约30%的求解时间。

2.2.3 蚁群算法

苏涛等[20]采用蚁群算法来解决TSP，并对蚁群数目m、信息启发因子α、期望启发因子β的不同取值进行比较，信息启发因子α取1～5，期望启发因子β取1～5，蚁群算法均能获得较好的搜索结果。Shi等[16]采用蚁群算法解决单配送中心、多车辆、多需求点的问题。郝瑞卿等[25]提出了混合遗传蚁群算法，利用遗传算法进行全局快速搜索产生初始解，将其转化为蚁群算法的初始信息素分布，随后利用蚁群算法的正反馈机制及并行性等特性高效求解问题的最优解。对混合算法与蚁群算法进行了比较，前者可有效解决遗传算法求解效率低及蚁群算法收敛过早的问题。

2.2.4 其他算法

王晶等[31]使用禁忌搜索算法直接解决了多配送中心、多需求点问题。张汉鹏等[22]提出了多起点迭代局部搜索算法解决两级车辆配送问题，针对主仓库发生灾害影响的情况，对单独策略、乐观协同策略、悲观协同策略、折中协同策略进行比较，折中协同策略效果最好。杜丽敬[38]通过平均权重法将三角模糊数转化为确定值，再采用基于非支配排序的差分进化(Non-dominated Sorting Differential Evolution，NSDE)算法求得Pareto最优解集。在基于雅安地震的实例中，NSDE算法在Pareto近似最优解集、收敛性、运行时间上优于遗传算法。Duan等[40]提出双层混合蛙跳算法求解双层车辆调度模型，与蛙跳算法、双层粒子群优化算法进行对比分析，优化效果更好。Hiermann等[30]提出了自适应大规模邻域搜索算法，与Cplex以及不包含标签算法的自适应邻域搜索进行对比实验，取得了更优的计算结果。

另外，Zheng等[48]对6种较新的进化(或改进)算法进行了对比实验：一是标准粒子群算法，具有局部随机拓扑和几个优化调整；二是自适应的差分进化(Self-adaptive Differential Evolution，SaDE)算法，其变异模式和控制参数通过从前几代学习而自适应调整；三是混合生物地理学优化(Blended Biogeography-based Optimization，B-BBO)算法，它通过混合迁移算子改进基本生物地理学优化算法；四是改进的遗传算法，由三个快速改进程序完成算法改进；五是基于梯度的局部搜索来获取准确局部搜索的粒子群算法(Gradient based Particle Swarm Optimization，GPSO)；六是采用全局迁移和局部迁移的组合来完成改进的生物地理学优化(Ecogeography-based Optimization，EBO)算法。在10个抢险救灾案例实验中，EBO和GPSO通常比其他4种进化算法表现更优，并且其性能优势随着问题维度的增加而增加，但在雅安地震这种大规模案例中，即使是EBO和GPSO也无法在规定时间内得到有效解。

2.3 多阶段求解及混合算法

王龙昌[18]提出了二级模糊综合判定法划分配送中心，利用双种群遗传算法对运输路径进行规划，再与捕食搜索算法相结合，动态改变遗传算子中的交叉和变异概率，更大程度地打破种群内部的平衡。改进算法得到的平均最优解优于标准遗传算法和并行遗传算法得到的结果。高啸峰[13]运用表上作业法确定各配送中心的配送范围，再运用改进的C-W(Clarke-Wright)节约算法优化车辆调度路线。姜海洋[26]采用优化的Dijkstra算法进行单源单汇问题求解，采用改进的C-W节约算法解决了单源多汇问题(即TSP问题)。何勇[32]先采用聚类算法把需求点分配给配送中心，再使用粒子群优化算法计算出最优的车辆配送路线。Zheng等[34]采用多目标禁忌搜索(Multi-objective Tabu Search，MOTS)算法解决任务分配、运输资源分配两个问题，采用多目标遗传算法(Multi-Objective Genetic Algorithm，MOGA)解决运输规划和车辆路径问题。在盈江地震实例中，该混合算法要优于多目标禁忌搜索算法、进化策略与差异编译算法、非线性多目标优化免疫算法、多目标差分进化算法。Chang等[39]先采用Dijkstra算法找到最短路径，再使用基于贪心搜索的多目标遗传算法求解配送路线。在基于台湾集集大地震的模拟运输中，该算法优于多目标遗传算法和标准贪婪算法。Yuan等[35]采用改进的Dijkstra算法求解第一种模型，采用蚁群算法求解第二种模型。在一个假设的20节点网络中，证明了算法的有效性。Barrachina等[23]在考虑车道数和车辆密度两种情况下，使用Dijkstra算法和进化策略解决路径规划问题。通过实验证明，基于密度的进化策略同时减少了运行时间和应急服务的到达时间，要优于Dijkstra算法和单纯的进化策略。

2.4 存在问题

从以上文献分析中可以看出，目前应急物资配送车辆调度优化算法的研究存在以下问题：

1)应急车辆调度是多目标多约束问题，涉及情况复杂，在实际配送中的突发情况难以预测，利用现有优化算法很难在规定时间内得到理想结果。大多数算法容错率较低，得出的优化结果并不能每次都满足配送要求，容易陷入局部最优。

2)大多数文献主要采用遗传算法、粒子群算法、蚁群算法等常用启发式算法解决应急车辆调度问题，较少文献对新兴算法及其混合算法进行研究，对新兴算法效率的评估不够充分。

3)在一些文献中对需求量、配送满足度、风险性等进行了模糊化处理，但由于缺乏规范化的数据收集和处理，得到的结果大都不理想，不具备可操作性。

4)目前，抢险救灾应急保障研究的大多数测试数据都是由计算机随机生成，只有小部分采用真实数据。而且，将启发式算法成功运用于救援行动的案例还是太少，多数求解结果不能完全满足决策者的需要。

3 应急物资配送车辆调度研究发展趋势

虽然未来的救灾行动更加复杂，但随着信息技术和计算机性能的快速发展，解决应急物资配送车辆调度问题越来越具可能性，以下几个方面值得关注：

1)当前各种应急车辆调度模型针对的问题单一，与实际问题有较大差距，不具有通用性。下一步，可采用系统工程的思路综合分析抢险救灾行动中的物资配送问题，找准关键的优化目标和约束条件，形成规范通用的应急物资配送模型，以满足决策者要求。

2)近年来，一批新兴的优化算法，如生物地理学优化算法、布谷鸟搜索、水稻田算法、仿生算法、烟花算法等，已经被提出并在各种问题中证明了有效性和效率。这些新兴算法，及其与现有算法的混合算法，在应急车辆调度问题上具有广阔的前景。但这些算法的特性还没有被充分了解，下一步可构建算法基准测试平台，对不同算法进行综合评估，以针对不同条件下的车辆调度问题，选择最适合的算法或其混合算法。

3)在采用优化算法对车辆调度问题进行求解的过程中，由于真实的应急车辆调度涉及因素较多，整个问题过于庞大，可以将其细分为多个阶段逐步进行求解，这不仅能够降低单个阶段的复杂性，而且能使决策者修正每个阶段的运算结果，使最终得到的配送方案更加符合实际需求。

4)大数据、云计算、人工智能等新技术应用可为应急物资配送车辆调度问题提供更多的解决思路。例如：通过大数据分析能够在海量信息中搜集、筛选出影响物资配送效果的关键信息；云计算可以极大地提高求解过程中的运算能力，使得高复杂度优化算法运行成为可能；通过模仿决策者的思维过程，人工智能可以根据应急态势的变化，尽快找到更符合当前需求的优化结果。

4 结语

本文重点围绕模型和优化研究两个关键点，综述了应急物资配送车辆调度问题的研究进展。通过对模型研究的分析，找到了影响应急物资配送车辆调度效果的主要因素，梳理出了在抢险救灾行动中车辆调度问题被广泛考虑的优化目标和约束条件。在优化研究分析中，对多类优化算法的应用效果进行了对比分析，指出了几种极具研究价值的新兴启发式算法及其混合算法。当前，应急物资配送车辆调度问题的研究已经在一定程度上提高了救援准确性和效率，但模型复杂度和优化求解速度之间的矛盾仍未能被很好地解决，随着信息技术和优化算法的发展，应急物资配送车辆调度的研究将进一步取得成果，也将在灾害救援中发挥更大作用。