基于竞价的租赁车辆资源分配和定价机制

刘旭东，张学杰，张骥先，李伟东，张 静

(1.云南大学 信息学院，昆明 650500； 2.云南大学 数学与统计学院，昆明 650500)(*通信作者电子邮箱denonji@163.com)

0 引言

汽车租赁公司通过购买车辆，然后将车辆共享给用户使用，汽车租赁出行是一种经济环保的出行方式。目前国内汽车租赁市场已成规模，据文献[1]显示，2015年中国汽车租赁市场依靠网络媒介的交易额超过90亿元，线下交易额达356亿元，而且汽车租赁市场的需求仍然巨大。另据文献[2]显示，2016年中国汽车销售量达到2 802.8万辆，汽车保有量近2亿辆，将为租车市场提供强有力支持。同时，大城市由于交通拥堵等问题，政府出台限号限行等措施来限制私家车的出行，也为租车市场的发展创造了良好的环境。此外，随着国内旅游业的迅猛发展，更加刺激着租车行业加速发展，可以预见汽车租赁行业的发展潜力巨大。

在有限的车辆使用年限内提升车辆的使用效率是汽车租赁公司主要的营收方式，但是目前线上汽车租赁平台主要通过传统的固定价格对车辆进行先来先服务的出租方式，车辆不能得到最有效的利用。首先，车辆采用传统的固定价格定价方式，租赁公司为了保证自己在每个时段都有利润，必须要维持较高的租赁价格，超过了用户预期，伤害用户积极性，将造成平台中车辆的闲置；其次，固定的价格不能够及时反映用户车辆供需关系，造成需求量大时车辆紧缺不能租出高价格，而空闲时车辆不能降价出租导致车辆闲置；最后，先来先服务的分配方式虽然可以保证分配的时效性，但是不能获得整体分配结果的最优，而且车辆的租赁周期最短也为一天，对实时性要求并不高。

所以本文将线上汽车租赁平台目前的问题总结为车辆分配的不优化与车辆定价的不合理。若将线上汽车租赁公司的车辆分配与定价问题进行合理改进，将为其提供更多的利润，更能加快汽车租赁市场的合理发展。

为了解决线上汽车租赁平台存在的问题，本文提出了基于竞价的租赁车辆资源分配和定价机制，主要包含三个方面：

1)可信的多需求拍卖机制设计。本文为在线汽车租赁平台设计了多需求的拍卖机制，用户可以对不同理想车辆提出自己的竞价，但最终结果只会满足每个用户一种车型。系统通过用户提交的请求来计算分配车辆，并且在线上汽车租赁平台中采用拍卖机制来实现车辆资源的分配和定价具有天然的优势，网络线上提交需求的过程，类似于密封拍卖，这也将保证用户提交的数据私密性。最后通过VCG(Vickrey-Clarke-Groves)的价格计算来保证拍卖机制的可信性。

2)基于网络流的车辆资源分配。车辆资源分配是一个RAP(Resource Allocation Problem)，需要先收集用户需求数据，然后使用合理的分配方法获得最优的利益。本文首先抽象出了租赁车辆分配问题数学模型，然后选择将问题等价于网络流图方式来找到该问题的最优解，解决车辆的最优分配问题。

3)合理的车辆资源定价。在拍卖机制中，定价问题是一个很重要的问题，既要考虑平台利益，也要满足价格的可信，公认的可信拍卖机制就是文献[3-5]提出的基于VCG机制的设计，并已被证明是可以保证在满足社会福利最大条件的同时又能够鼓励可信竞价的典型机制，所以本文将采用VCG的定价机制来计算用户的最终支付价格。

1 相关工作

本文使用竞价的方式解决线上汽车租赁平台的车辆分配和车辆定价问题。对于拍卖机制的研究应用有很多，但在汽车租赁方向还没有相关的研究工作；车辆分配与调度问题在网约车平台中研究较多，而定价机制则研究得较少。

1)拍卖机制。使用拍卖机制对商品进行定价已经持续了很长时间，而其中最重要的研究无疑是由Myerson[6]提出的最优拍卖机制。拍卖的机制在现代已经成功应用于很多商业领域，并提供了不菲的商业利润。如在美国联邦通信委员会(Federal Communications Commission，FCC)的频谱拍卖资料[7]中显示，截至2015年9月30日，FCC已经完成了87次频谱拍卖，拍卖所得总金额超过949亿美元。在广告竞价拍卖中，Google依靠关键词竞价拍卖的收益占到了其90%以上的收益，并且使用第二竞价进行关键词的拍卖竞价。同样，作为全球最大的社交网站Facebook则主要采用基于VCG的拍卖竞价方式进行广告的拍卖，并获得了巨大的收益。而最近在云资源平台快速发展的情况下，拍卖机制也被广泛应用于网络云资源的竞价拍卖中，其中最好的例子就是亚马逊弹性计算云(Elastic Compute Cloud，EC2)云资源平台。张骥先等[8]提出了一种支持云计算虚拟资源分配的可信多需求机制，可以使资源提供商获得更大的收益，并且得到了很好的实验效果。此外，Zaman等[9]提出了基于联合竞拍的动态云资源分配，将云资源中如内存、CPU、硬盘等作为用户争夺的资源，然后使用拍卖机制来进行动态的云资源分配与定价。在云资源平台的不断发展中，文献[10]提出了双向拍卖的云资源拍卖机制，而文献[11]提出了多个云平台协同共享资源的联盟云资源拍卖机制，即用户提交的资源请求可以被多个平台接受并协同分配，所以在本文的基础上，未来可对竞价租车双向拍卖或者网点协同合作拍卖进行相关研究。

尽管拍卖已经成功应用于很多领域，但目前还没有被应用在线上汽车租赁平台中，本文则考虑构建可以在线上汽车租赁平台中使用的模型。

2)资源分配。车辆分配问题在网约车中使用得较多，网约车在国内互联网的高速发展下获得了极大的发展，甚至改变了人们的交通出行方式，如滴滴等交通出行应用的兴起，越来越多的人使用手机叫车出行，使得网约车成为当代人交通出行中不可缺少的方式。而研究发现，线上汽车租赁与网约车的形式基本相同，都是通过用户发出需求，平台计算分配车辆给用户，最后通过平台来支付完成订单。但是它们所追求的目的不同，网约车更注重订单的实效性，线上汽车租赁将更多地考虑平台车辆是否能够合理有效分配。目前线上汽车租赁的相关研究较少，可以通过类比网约车车辆资源分配问题来讨论线上汽车租赁车辆的分配问题。

网约车的车辆资源分配相关内容主要集中在用户订单分配与车辆的分配。Zhang等[12]在解决网约车的订单分配中提出了使用就近分配原则，即当出现车辆竞争订单时，对订单进行了就近调度。就近调度的好处在于可以在短时间内完成订单的分配，但是存在就近调度订单不一定是全局最优订单的问题，如一个用户分配到距离其最近的车，而附近的车辆可能需要走更远的距离去接其他乘客。而Seow等[13]提出的NtuCab则追求订单等待时间和订单安排接送距离的最小化，将每个代理机构看作是一个计算单元，每个计算单元拥有N个订单/车辆对，每个订单只能满足一个车辆，而当司机不愿意接单时，会将订单发给另外一辆车。对于车辆的调度，Glaschenko等[14]设计了出租车实时调度系统，由于车辆实时调度系统有很多复杂性问题，如车辆多、订单大等，造成了解决调度问题的困难，该文献中使用元启发算法Meta-heuristics解决调度问题，并且计算的时间在可接受范围之内。但是在线上汽车租赁平台中，并不需要实时调度，更多地是要寻找最优的分配方案，所以这些网约车调度方案并不适用。同时，使用竞价的方式进行资源分配已经成功应用在了云资源中，如Liu 等[15]提出了使用竞价对不同虚拟机进行分配的方法。

3)车辆的定价。在近代拍卖机制研究中已经对定价方式已经作了深入的研究。Maskin等[16]认为要考虑规避用户的风险，并认为第一竞价就是最有利的标准拍卖机制。而Milgrom等[17]分析了拍卖竞价并不是孤立的，用户的竞价会根据其他人的竞价而改变，并表明了最有利的标准拍卖竞价是第二竞价，而第二竞价也被广泛地应用到了基于竞拍的应用中。而由Vickrey、Clarke和Groves三人共同提出的VCG拍卖定价机制无疑是定价机制的里程碑，已经被证明是最有效的拍卖定价机制，VCG拍卖机制的出现提供了一种可信机制的拍卖框架，并且应用于诸多领域，如文献[18]将VCG机制应用在P2P存储系统中，使得竞价者完全根据自己的意愿来进行出价，而没有提供虚假竞价的理由，即用户提交虚假竞价时不会得到好处。

综上，基于竞价的机制设计已经应用于不少领域，但目前还没有应用在汽车租赁平台中。将竞价机制应用到线上汽车租赁平台中，车辆的合理分配与车辆价格制定问题都是需要解决的重点与难题。本文研究一种可信的竞价机制，旨在解决车辆分配与车辆的价格制定问题。

2 系统模型和前期准备

本文借鉴云平台中的资源模型提出了租赁汽车分配的数学模型，该模型主要根据竞价模型抽象了汽车租赁平台的车辆资源与参与竞价用户需求的情况。之后，根据该数学模型构造了最大社会福利的数学规划函数，根据汽车租赁的现实情况，本文考虑车辆总数与用户最多只能竞价成功一辆车的基本限制条件。以后也可以研究增加时间、地点等多维度的限制条件，增加模型的实用性。

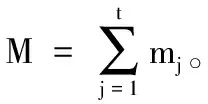
其次，用户i∈U将根据平台提供的信息提交自己的车辆车型需求请求，记用户i提交的请求为Qi=(Ri,Bi)。其中：Ri=(ri1,ri2,…,rit),rij∈{0,1}(j=1,2,…,t)表示用户对每种车型的请求；Bi=(bi1,bi2,…,bit),bij∈Ri表示用户对不同车型的竞价。

为了清晰描述模型信息，本文根据系统模型构建了如表1所示的汽车租赁平台车辆资源以及用户竞价请求来举例说明本文的数据模型。

表1 汽车租赁平台车辆资源与用户i提交的需求

由表1可知，平台共提供三种车型，每种车型的数量分别为m1=2,m2=3,m3=1,每种车型闲置成本为c1=10，c2=15，c3=20。用户需要根据不同车型的情况来提出不同的请求，如表1中用户提交的请求为Ri=(1,0,1),表示选择车型1和车型3，Bi=(29,0,35),即用户对车型1的出价为29，车型2的出价为0，车型3的出价为35，所以，该用户提出的请求为Qi=((1,0,1),(29,0,35))。

汽车租赁平台想要达到的目标就是如何分配这些有限的车辆资源给用户，能够在尽量满足用户需求的同时，还能使平台获得的利润最高。构建数学规划模型如式(1)所示：

(1)

(2)

(3)

规划函数(1)表示：循环每个用户提交的对每种车型的请求，规划出一种能够使得汽车租赁平台利益最高的方案。

规划函数(1)的限定条件分别是：式(2)表示每个用户只能满足一个车型，式(3)表示每种车型满足的用户数目不能大于平台提供的该种车型的数量。

3 基于竞价的车辆租赁资源分配及定价机制

由于式(1)中的数学规划模型与基于竞拍的拍卖机制的数学模型基本一致，因此考虑使用基于竞价的拍卖机制来解决这一问题。本文设计了一个在线汽车租赁算法来计算租车平台中车辆的分配与用户需要支付的价格。车辆的分配算法利用基于网络流的分配算法求解数学规划(1)中的规划最优解，即拍卖模型中的社会福利最大解。该算法主要是基于最小费用最大流的网络流算法，获得最大收益(最小费用取反)的同时尽量多地满足用户的(最大流)需求，用来分配用户的线上汽车租赁的提交请求。

3.1 租赁车辆VCG拍卖算法

按照最优机制设计，本文提出了租赁车辆VCG拍卖(VCG-Car Rental Auction, VCG-CRA)算法。算法主要包括两个部分：首先是租赁车辆分配算法(CRA_Allocation)，根据用户提交的请求进行车辆的分配；然后通过租赁车辆定价算法(CRA_Pay)计算用户需要支付的价格。

算法1 VCG-CRA。

输入 车型T包括每种车型的数量mj,车辆的使用成本cj；所有用户的需求信息Q=[(R1,B1),(R2,B2),…,(Rn,Bn)];

输出 参与竞价被选中用户及对应车辆X=[x10x11…x1t…xnt],总社会福利SW，被选中的用户需要支付的价格P=[p1p2…pn]。

{用户请求预处理}

1)

for allQi,i∈Udo

2)

ifbit

3)

rit=0

4)

bit=0

5)

end if

6)

end for

{车辆分配}

7)

X,SW←CRA_Allocation(Q,T)

{价格计算}

8)

P←CRA_Pay(Q,X,SW,P)

由算法1可知，首先需要等待收集所有用户提交的用车请求，之后需要对用户竞价进行预处理，即当用户对某一个车型出价低于车辆的闲置成本价时，将此用户的竞价数据直接改为0，即删除这个用户对此车型的竞价(1)～6)行)。这样既保证了后面计算的有效性，也提高了之后算法的计算效率。然后，使用CRA_Allocation算法进行车辆的分配。最后再使用CRA_Pay算法来计算每个用户真正需要支付的价格。

3.2 基于网络流的车辆分配算法

根据式(1)中的数学模型与式(2)和(3)的限制条件，要解决的问题就是在车辆限制条件下求解得到最大的费用流，这与经济学中的最小费用最大流问题相似。最小费用最大流的网络中每段路径都有“容量”和“费用”两个限制的条件，研究试图寻找出：流量从起点S到终点E，如何选择路径、分配经过路径的流量，可以在流量最大的前提下，达到所用费用最小的要求。本文模型的要求是要达到的所有费用最大，所以将每条路径中的“费用”都取负值，而整体的模型要求就转化为最小费用最大流的模型。图1是根据本文模型构造的最小费用最大流的有向图。

图1 最小费用最大流(容量，费用)有向图

由图1可以看到，该图由多条从起点顶点S到终点顶点E的不同路径组成，每条边的内容分别指经过这条边的容量和费用，第一组顶点从1到n表示的是用户，第二组顶点从1到t表示的是车型。最小费用最大流算法的目的就是找出满足容量限制和费用最小(本文的需求其实是要费用最大，而该算法计算的是最小费用，刚好相反，所以这里将用户费用边取负值，即可按照最小费用最大流求解，之后再将结果取反即可)的路径的一个集合，这个集合刚好就是满足本文模型分配的要求，即满足平台利益的同时又不超过车辆的数目。

定理1 数学规划(1)的最优解的目标函数值与图1中的最小费用最大流的目标函数值的绝对值相同。

因此，数学规划(1)的任一可行解对应于图1的一个可行流，且其目标函数值的绝对值相同。

证毕。

求解最小费用最大流算法采用了贪心法的思想，即每次找到从起点S到终点E的一条路径，判断该路径是否为增加流量后的费用最小的路径，直到没有这样的路径。在寻找起点S到终点E的路径时，由于网络中“费用”都是负值，所以本文算法将使用文献[19]提出的最短路径快速算法(Shortest Path Faster Algorithm， SPFA)来实现。

定理2 最小费用最大流得到最优解是数学规划(1)的最优分配算法。

证明 最小费用最大流通过在所有增广路径(可行流)中寻找单源最短路径(最小费用)，最终将找到符合限制的最优解，而最小费用最大流与数学规划(1)等价，所以将计算得到数学规划模型的最优解。

最小费用最大流的CRA_Allocation算法如算法2所示。首先需要初始化图数据(1)～23)行)，将平台资源情况与收集的用户请求转化为邻接矩阵G；之后通过寻找图中所有满足流量的路径(最大流)，再使用SPFA单源最短路径算法寻找出单元最短路径(最小费用)，并保存路径到图G*(24)～26)行)；然后计算将图G*转化为车辆分配向量X与车辆分配价格向量P(27)行)，再计算当前分配的资源社会福利值SW(28)～31)行)；最后返回车辆分配向量X、车辆分配价格向量P与当前分配的资源社会福利值SW。

算法2 CRA_Allocation算法。

输入 车型T包括每种车型的数量mj,车辆的使用成本cj；所有用户的需求信息Q=[(R1,B1),(R2,B2),…,(Rn,Bn)]；

输出 参与竞价被选中用户及对应车辆X=[x10x11…x1t…xnt],总社会福利SW。

{初始化图数据，邻接矩阵G=(V,E)}

1)

G←0

2)

for allU,i∈Udo

{源点到车型，节点矩阵N，费用矩阵C，流量矩阵W}

3)

G←N[0][i+1]=1;

4)

G←C[0][i+1]=0;

5)

G←W[0][i+1]=1;

6)

end for

7)

for allQi,i∈U,j∈Tdo

{用户到车辆，节点矩阵N，费用矩阵C，流量矩阵W}

8)

ifrij=1 then

9)

G←N[i][n+j]=1;

10)

G←C[i][n+j]=-bij;

11)

G←W[i][n+j]=1;

12)

end if

13)

end for

14)

for allT,j∈Tdo

{车型到终点，节点矩阵N，费用矩阵C，流量矩阵W}

15)

G←N[n+j][n+t]=1;

16)

G←C[n+j][n+t]=0;

17)

G←W[n+j][n+t]=mj;

18)

end for

{寻找图G中所有满足流量限制的增广路径l(最大流)}

19)

for allG,l∈Gdo

{增广路径不存在则跳出循环}

20)

ifl==0 then

21)

break

22)

end if

{查找该增广路径l中的最短路径(最小费用)，存储到图G*=(V*,E*)}

23)

G*←SPFS(l)

24)

G-l

25)

end for

{得到最优分配X,与分配用户出价P}

26)

X,P←G*

{计算当前分配的社会福利SW}

27)

SW←0

28)

for allxij=1,i∈U,j∈T

29)

SW=pj+SW

30)

end for

31)

ReturnX,SW

3.3 基于VCG的CRA_Pay支付价格算法

最后虽然用户根据自己的心理预期价位提交了自己的租车请求，但实际上的租车费用会根据一些情况而变化，例如上下班高峰时间，用户的心理价位不能代表当时的租车费用，因此，这里采用可信的VCG定价方案来计算出用车时实际费用的多少。

VCG竞价方案是公认的最佳竞拍定价方案，它定价的核心理念就是计算用户的社会福利，用户需要支付的价格与自己的出价没有关系，这样就可以保证用户出价的真实性，这样用户就没有必要通过恶意出价来破坏竞价环境，而根据其他人当时提交价格的情况来计算实际费用，也更能够说明当时竞价时刻的供求关系，计算得到的费用将更加准确。因此在算法中需要计算出该用户不参与竞价和该用户参与竞价但是出价为零时的不同情况，所以VCG算法的计算时间复杂度较高。VCG算法模型如下：

1)A是车辆最优分配算法;

算法3 CRA_Pay算法。

输入 车型T包括每种车型的数量mj,车辆的使用成本cj;所有用户的需求信息Q=[(R1,B1),(R2,B2),…,(Rn,Bn)]，用户车辆分配结果X=[x10x11…x1t…xnt]，总社会福利SW;

输出 最终用户需要支付的价格，P=[p1p2…pn]。

1)

X*←0

2)

SW*←0

{计算每个被分配用户不参与竞价和参与竞价且竞价为0}

3)

for eachi←{i|xij∈X,xij≠0},i∈Udo

4)

(SW*,X*)←CRA_Allocation(Q,T)

5)

pi←SW*-(SW-bij)

6)

end for

7)

ReturnP

定理3 最优拍卖机制是可信的。

证明 车辆资源分配算法采用最小费用最大流算法求解出最优解，文献[20]证明了在满足资源分配最优解的情况下使用VCG进行价格计算一定可以满足拍卖机制是可信的，因此最优拍卖机制是可信的。

此外，考虑到使用了最小费用最大流模型进行车辆分配算法可以得到最优解，即解的集合可以保证当前分配结果的社会福利最大，所以在使用VCG算法计算用户i的出价时，可以保证用户i最后的出价结果一定是小于等于自己的竞拍价格的(若大于说明还有最优解，即用户i在不参与竞价时还有比其更高竞价)，该算法对平台与用户利益都能保证。

综上，本文使用竞拍的方式解决线上车辆租赁的车辆分配与定价问题，最优车辆分配算法采用最小费用最大流模型进行计算，最优支付算法可以按照VCG机制计算规则来设计。接下来将举简单实例具体说明机制的执行过程。

3.4 算法举例

设一个线上汽车租赁平台某天能提供的车辆车型和数目如表2所示，提供的车型有(真实情况为真实的车型号，这里为了方便理解，采用了不同档次名称表示)：经济型、舒适型和精英型各1辆。表2中还列出了经过用户预约竞价后，服务器收到的用户请求。

表2 用户1到用户5提交的竞价需求

根据表2的数据绘制了关于表2的最小费用最大流(容量、费用)图如图2所示。

图2 表2数据最小费用最大流(容量，费用)图

首先，为了转化为本文的模型，需要将费用全部取反，然后如图2所示，每条边代上的权值为该路径的容量和价格，图中一共有10个顶点，其中起点是顶点0，终点是顶点9，顶点1～5表示用户1～5，而顶点6～8表示三种不同的车型。该模型要寻找的问题就是在不超过每条边容量的情况下，求得从起点到终点的路径费用最少(这里将用户的竞价取为负，就可以得到的路径费用最大)。

根据数据可以计算得到满足条件的三条路径分别是：0→1→6→9，该路径的费用为20元；0→3→8→9，该路径的费用为45元；0→4→7→9，该路径的费用为26元。所以竞价成功的分别是用户1、3、4，三条路径合计平台的最大收益为91元，为最大收益，而且在满足用户需求的同时也没有超过平台额定的车型数目。

之后，根据分配模型，给每个用户都分配到了车辆，接着需要计算每个用户真正需要支付的价格。

首先，计算用户1需要支付经济型车型的价格，根据VCG算法，先要计算用户1不参与竞价时的分配情况，根据分配算法得到三条路径分别是：0→2→6→9，竞价为20； 0→3→8→9，竞价为45；0→4→7→9，竞价为26。即用户2竞拍到经济型车型的竞价为20元，用户3将竞拍到精英型车型的竞价为45元，而用户4拍到舒适型的竞价为26元，此时的总社会福利为91元。之后，计算用户1参与竞价，但是出价为0的情况，可知总社会福利为71(=91-20)元，所以用户1只需要支付20(=91-71)元，大于经济型车型的闲置成本，所以用户1最后要支付的价格为20元。

然后，计算用户3需要支付精英车型的价格，首先，也要计算用户3不参与竞价时的分配情况，根据分配算法得到三条路径分别是：0→1→6→9，竞价为20；0→5→8→9，竞价为44；0→4→7→9，竞价为26。即用户1竞拍到经济型车型的竞价为20元，用户5竞拍到精英型车型的竞价为44元，用户4拍到舒适型的竞价为26元，此时的总社会福利为90元。之后，计算用户1参与竞价，但是出价为0的情况，可知总社会福利为46(=91-45)元，所以用户1只需要支付44(=90-46) 元，大于精英车型的闲置成本，所以用户1最后要支付的价格为44元，比自己的竞价要少1元。

最后，计算用户4需要支付舒适车型的价格，用户4在不参与竞价时重新规划路径为：0→2→6→9，竞价为20；0→3→8→9，竞价为45；0→1→7→9，竞价为25。即用户2竞拍到经济型车型竞价为20元，用户3竞拍到精英型车型的竞价为45元，而用户1拍到舒适型的竞价为25元，此时的总社会福利为90元。之后，计算用户5参与竞价，但是出价为0的情况，得知总社会福利为65(=91-26)元，所以用户5只需要支付25(=90-65)元，大于舒适型车型的闲置成本，所以用户5最后要支付的价格为25元，同样比自己的竞价要少1元就可以拍到此车型。

4 实验与分析

4.1 实验设计

本章通过实验来评估本文机制是否合理有效。对于线上车辆租赁平台的车辆分配与定价问题，目前没有相关文献能够提供有效的实验方法来进行评估，所以，为了体现利用拍卖机制的分配与定价合理有效，本文将模拟不同租车网点的车型车辆情况，采用随机样本数据订单对机制进行实验测试，实验数据模拟用户订单完全随机产生。实验搭建在Intel i7-4710MQ 2.5 GHz,8 GB内存平台。实验设置如下：

1)数据上，本文根据一嗨租车中的租车点提供的车量、车型数据进行模拟实验，主要通过对北京、上海租车点的车辆规模进行了统计，得出每个网点平均有15种车型供用户选择，按照每种车型4～5辆计算，车辆总数大概在100辆左右，表3为实现使用的平台资源数量。

2)根据统计车辆的数据结果，模拟了不同用户量、不同规模的请求，每个用户都提出自己的车辆需求，且用户平均提交的车辆需求订单为总体车辆的40%。

3)实验数据采用随机数，用户出价按照车辆成本为基准随机加减。每组数据进行多次实验，结果取均值。

4)使用Java语言实现先来先服务(FCFS)、最大利润优先(MAXBENIFIT)算法与本文的VCG-CRA算法。

实验将考虑如下问题来评估VCG-CRA算法：

1)评估指标。由于目前没有基于竞价机制的汽车租赁相关文献与评估指标、方法，本文根据汽车租赁行业与计算机算法的重点关注指标，设计使用以下三个指标来衡量本文算法的实验结果：订单成功率、平台收益和计算效率，这些指标虽然不能全面考量算法的性能，但也能够说明算法应用于汽车租赁平台中提升的效果。

2)算法对比。本文将考虑通过先来先服务与最大利润优先的算法进行对比实验，说明不同算法情况下的效果。

3)不同规模、不失一般性实验。实验主要以用户数量分为不同规模：小规模(300个用户)、中规模(500 个用户)和大规模(1 000 个用户)进行测试，测试研究不同用户数对算法的影响。此外，还以平台车辆数分为不同规模，具体研究用户数与平台车辆规模对VCG-CRA算法效率的影响程度。

表3 不同用户规模的线上汽车租赁平台资源

4.2 实验结果

4.2.1 订单成功率

订单成功率是网约车最关心的指标之一，因为订单的成功率一定程度上直接影响用户体验度，而用户的体验度将直接影响平台的用户量和平台收益，所以如何能最大化地使得用户都分配到自己预约的车辆，是每个平台都要优先考虑的。

先来先服务(FCFS)调度算法在计算机中很常见，而目前线上租赁行业也基本都采取这样的方式来出租车辆，先来先服务算法的好处是简单、容易实现，但这样的分配方式并不利于平台的车辆分配。最大利润优先(MAXBENIFIT)算法是顺应平台要求利润最大化诞生的，在收集了所有用户数据后，很自然地想到可以考虑优先满足最大竞价者，但这样的局部最优并不一定是全局最优解。不同算法的订单成功率比较如图3所示。

图3 不同算法的订单成功率比较

从图3可以看到，在模拟线上车辆租赁平台的数据中，VCG-CRA算法与最大利润优先(MAXBENIFIT)算法在三种不同规模的用户量下都可以满足所有车辆的分配，达到100%的车辆分配；而先来先服务(FCFS)算法的订单成功率只有70%～80%，会造成车辆分配的不均，导致车辆的闲置。由于目前线上车辆租赁平台大多采用类似先来先服务(FCFS)的算法模式，所以VCG-CRA算法与最大利润优先(MAXBENIFIT)算法在车辆的分配效果上都比目前模式好，比先来先服务算法提高了20～30个百分点。

4.2.2 平台收益

经过最小费用最大流算法的计算，可以得到最优的车辆分配及平台可以获得的最大收益，但是最大收益情形下的用户请求不是可信的。通过可信的VCG价格的重新计算，会牺牲部分平台的收益，换取可信合理的用户价格，将会根据用户需求量而变动。

图4是不同算法得到的不同的收益情况，可以看到，通过最小费用最大流算法得到的平台收益是最高的，是最优的分配方式，而先来先服务(FCFS)算法得到的平台收益最低，只有最小费用最大流算法收益的60%左右；通过最大费用优先(MAXBENIFIT)和VCG算法计算得到的平台整体收益都比较高，其中最大费用优先(MAXBENIFIT)算法可以得到最小费用最大流算法95%左右的收益，VCG-CRA算法也可以达到其90%以上的收益，比先来先服务算法的平台收益提高了30个百分点。而且最小费用最大流算法、最大费用优先(MAXBENIFIT)算法和VCG-CRA三种算法的收益情况都比较稳定，而FCFS算法的收益有波动情况。

图4 不同算法的收益比较

4.2.3 计算效率

由于租车平台的要求,用户最短的使用周期都在1天，所以线上汽车租赁平台对于计算效率的要求并不是很高，但是本文算法仍然需要考虑计算车辆分配以及定价所花费的时间，以便全面评价算法效果。

如图5中所示，车辆分配算法的执行时间其实很短，其中先来先服务(FCFS)算法的执行花费时间最短，三种用户规模下基本30 ms内就可以完成分配，而最小费用最大流算法因为需要寻找最优的分配，所以耗时比较长，需要60 ms左右的时间；而花费时间最多的是VCG-CRA算法，由于每个用户都需要重新分配计算所有用户的竞价，所以需要执行多次分配算法，可以看到在模拟数据中，为用户计算最后应付价格花费的时间大概是1 s左右，还在可以接受的范围内。此外，随着用户规模数的增加，无论是分配算法还是价格计算，都需要花费更多的时间，最小费用最大流、先来先服务(FCFS)与最大费用优先(MAXBENIFIT)的分配算法都增加了少量执行时间，而VCG-CRA算法价格计算执行的时间增长呈倍数的增长，从300用户到1 000用户的用户规模，最小费用最大流算法的执行时间从50 ms增加到了90 ms，耗时增加了156%，而VCG-CRA算法却从原来消耗566 ms增加到了1 846 ms，增加了300%，可见VCG-CRA算法价格计算的执行效率对用户数量很敏感，随用户量的增加，执行时间增长很快。

图5 不同算法的执行时间比较

为研究VCG-CRA算法的执行速度是否也受到网点资源数目的影响，接下来还进行了不同规模组的不同网点的实验。

如图6所示，算法时间的消耗随用户数与车辆数的增加而增长。当车辆数一定时，随着用户的成倍增加，算法的时间消耗增长速度基本一致，如150的车辆数中，随着300、500、1 000用户规模的增长，算法的执行时间基本成倍地增长；而当用户数一定时，随着车辆数目的增加，算法的执行时间增长很快，可以看到车辆数翻倍的情况下，时间的消耗有近400%的增长。所以综上，平台车辆数目的增加对于算法计算的影响更大。

图6 不同规模(用户×车辆数)计算耗时比较

在线汽车租赁平台中车辆的出租周期最短都为1天，所以实验中的时间消耗可以接受，车辆的租赁也会根据不同区域的网点来分配车辆，所以一般不会有太大规模的车辆数来参与计算。

因此基于竞价拍卖机制的在线汽车租赁机制可以有效应用于在线汽车租赁平台，该机制能够完成最优的车辆分配与合理的价格制定，并且计算时间效率在可以接受的范围内。

5 结语

本文针对线上车辆租赁平台的问题进行建模，使用基于竞价的机制设计，来解决平台车辆分配与车辆的定价问题。从理论分析和仿真实验结果以及对比其他算法也可以看出，本文算法允许用户对不同车型提交竞价，能够使得平台的车辆最优地分配给不同用户，并且在车辆的定价上，可以在保证用户可信出价的同时，合理地根据用户需求为车辆进行定价，具有车辆最优分配、合理定价的优势。最终实验表明，本文算法取得了很好的结果，能有效提高线上车辆租赁平台的车辆使用率。在未来的研究工作中，拟加入附近的租车网点，形成网点联盟，提高竞价机制的实用性与网点车辆的使用效率。