基于随机森林回归分析的径流预报模型

(河南省南阳水文水资源勘测局，河南 南阳 473000)

径流预报是水利水电工程设计、施工和运行管理的重要依据，在防洪减灾、水资源优化配置等方面发挥着显著的作用[1]。因此准确有效地延长径流预见期、提高径流预报精度有着至关重要的意义[2-3]。目前，水文学者对径流及其影响因子的关系进行了大量的研究[4-6]，常用的有多元回归模型、逐步回归模型、最小二乘法等，但是受天文、气候、植被、地质地貌等因素的影响，水文预报呈现出随机性、高维性、模糊性等特点[7]。随机森林回归(Random Forest Regression，RFR)算法是由L. Breiman等[8]于2001年共同提出的一种基于决策树的集成学习算法，可以同时处理连续、离散属性，具有运行效率高、防止过拟合、强稳健性和抗噪性等优点，但是该方法在水文领域应用较少。因此，本文选取1970～2010年西峡水文站年降水量、年蒸发量、年平均流量、年均气温、年均相对湿度和年均气压作为预报因子，基于R语言构建随机森林回归算法，建立径流预测模型，为实际工程中径流预测问题的研究提供技术支撑。

1 数据和方法

1.1 数据来源

本文的分析数据主要来源于西峡水文站1970～2010年的水文及气象数据，主要包括流量、径流量、降水量、蒸发量、气温、相对湿度和气压等资料。西峡水文站系长江流域丹江水系老灌河干流上的主要控制站，为国家级一类站，控制流域面积3 418 km2，区间干流长度165 km，多年来平均降水量846 mm。

1.2 随机森林回归

(2)随机子空间。在构建回归决策树的过程中，每个分裂节点在特征空间中随机选择若干特征构建特征子空间,并选出最优特征子空间进行分裂，保证树的独立性和随机性。在RFR中，树的个数(ntree)和随机特征数(mtry)决定着模型的最终预测能力。

1.2.1 预报模型构建

(1)样本划分。以选取的6个预报因子作为解释变量，以西峡水文站年径流作为目标变量，划分1970～2000年数据为训练样本，2000～2010年数据为验证样本，采用训练样本构建预报模型，利用检验样本对模型预报精度进行评价。

(2)预报模型构建。基于R语言的randomForest函数构建随机森林模型[9]，其中mtry默认为输入变量的1/3，本文选取变量有6个，则mtry值取2。通过实验得到不同决策树个数的模型误差与ntree的关系(如图1所示)，模型错误率随着ntree的增加逐渐降低，错误率在ntree为300时达到最低(2.92%)，之后随着ntree值的增加，模型的错误率仍保持较低且稳定的状态。该特征充分证明了RFR算法具有防止过拟合的能力。

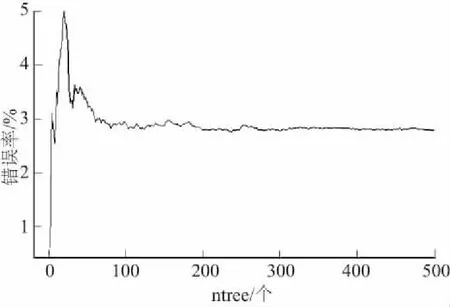
图1 不同ntree对应的模型错误率

考虑到模型的精度和运算效率问题，实验最终选择mtry=2，ntree=300进行建模。

1.2.2 模型变量重要性评价

RFR通过计算解释方差百分比(variance explained)来评价模型的预测能力。用方差增量(increase in mean squared error,IncMSE)以及节点纯度增量(increase in node purity, IncNodePurity)两个指标来定性衡量特征变量对目标变量的重要性。IncMSE为采用随机变量替换某一变量对模型预测结果的影响，若该随机变量使方差显著改变，则表示原变量相当重要；IncNodePurity则利用同质性增加原理来衡量变量的重要性[9]。

1.2.3 模型评价与检验

本文通过评价模型的拟合效果和检验模型预测结果来评价模型的预测能力。通过计算RFR模型的决定系数(R2)和均方根误差(RMSE)来评价模型的拟合效果[10]。

(1)

(2)

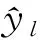
分别对RFR模型预测结果进行检验，通过计算总体相对误差(Rs)、平均相对误差(E)、平均相对误差绝对值(E′)3个统计量指标以及精度P来评价模型的预测能力[10]。

(3)

(4)

(5)

(6)

2 结果分析

2.1 特征变量重要性评价

随机森林算法可以用来评估所选特征变量的重要性，有效避免了一般回归问题面临的多元共线性问题[11]。本文特征变量的重要性评价如表1所示。可以看出年平均流量、年蒸发量、年降水量、年平均相对湿度对于径流模型的预报有较大的贡献。

表1 RFR模型变量重要性评价 %

2.2 精度评价分析

2.2.1 模型评价

通过实验得到预测模型的均方根误差(RMSE)为 0.0382，决定系数(R2)为0.89，可知模型预测精度较好。

2.2.2 模型检验

RFR模型预测结果如表2所示，检验数据的平均相对误差在16%以内，精度较高。

表2 径流量模型预测检验结果

通过计算模型偏差统计量评价模型的预测能力，结果如表3所示，可以看出模型预报能力较好。

表3 模型总体预测结果检验

3 结 论

(1)本文建立的RFR径流预报模型R2为 0.89，RMSE为 0.038 2，模型的拟合效果较好；模型预测结果的总相对误差为0.034，预测精度P为91.52%。综上表明本文构建的RFR径流预报模型预报能力较好。

(2)在多样本、多指标、复杂的水文预报问题处理中，RFR算法可以评估各个特征变量的重要性，对离群值不敏感，在随机干扰较多的情况下表现稳健，且不易产生过度拟合。而且RFR算法包含估计缺失值的算法，在水文资料存在缺失的情况下(1971～1975年有资料缺失)能够弥补缺失值，使预测结果仍可维持较高的精度。