非零位凸非球面子孔径拼接检测技术研究

闫公敬，张宪忠

(齐齐哈尔大学，黑龙江 齐齐哈尔 161000)

1 引 言

非球面光学元件在光学系统中能够校正像差，提升像质，同时可以减小光学系统的尺寸与质量，其作为光学系统的核心部件被广泛应用于各个领域[1,2]。

对于凹非球面镜，基于无像差点、补偿器、CGH(Computer Generating Hologram)等补偿手段通常可以完成凹面镜的全口径检测。然而对于凸非球面镜，若直接进行全口径检测则需要口径更大的补偿元件，例如口径更大的Hindle球、补偿器、CGH等。这些辅助元件的尺寸甚至为检测凸非球面的几倍，这就对材料与工艺造成了难度[3-5]。

子孔径拼接检测作为一种以小检大的测量手段，被广泛应用于大口径平面镜，球面镜，非球面镜的检测。国外对拼接检测的研究起源于20世纪80年代，由亚利桑那大学的C.J.Kim提出。亚利桑那光学中心与QED公司均对拼接检测进行了比较深入的研究。其中亚利桑那光学中心的苏鹏博士提出了一种绝对拼接检测算法，该算法可以在拼接检测中实现标准镜与被检测面的误差解耦[6]；QED公司研制出了球面拼接仪SSI(Subaperture Stitching Interferometer)与非球面拼接仪ASI(Aspherical Stitching Interferometer)，可以实现对非球面镜的拼接检测[7,8]。国内对拼接检测的研究起源于20世纪90年代，研究主要还停留在拼接算法上，其中国防科技大学的陈善勇等人对非球面拼接的几何方法进行了研究[9]，成都光电所的候溪等与浙江大学的田超等人对环形子孔径拼接技术进行了理论研究[10-11]，长春光机所的王孝坤等人基于全局优化算法对拼接检测进行了理论研究[12]，上海光机所的郭福东等人对拼接中的快速调整做了理论研究[13]，浙江大学的刘东等人在自由曲面拼接检测方面进行了研究[14]。

本文主要针对凸非球面非零位拼接检测进行了研究，建立了相应的算法模型，并基于上述模型对一凸非球面进行了拼接检测，验证了拼接的可行性与精度。

2 拼接模型

拼接算法的流程如图1所示。

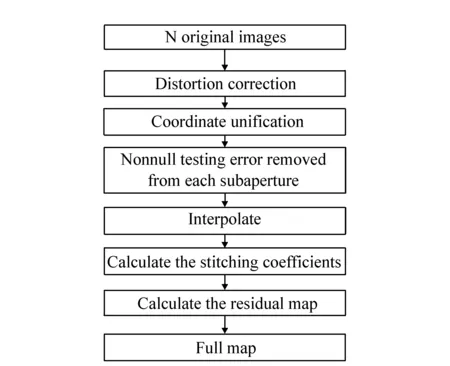
图1 子孔径拼接流程图 Fig.1 Flow chart of sub-aperture stitching testing

首先对被检非球面镜进行子孔径规划，而后对各规划子孔径进行畸变校正。

根据被检测各子孔径的相对位置完成各子孔径在全局坐标系内的对准后，即可对各子孔径进行非共路误差计算。

在非球面非零位检测中，利用标准球面镜对非球面镜进行检测时，由于检测中各光线并非沿镜面法线入射，则检测结果中会出现由于非球面相对球面的偏离造成的波像差。

对于同轴非球面，上述误差主要是球差，其形式如图2所示，对于离轴非球面，上述误差形式中主要是像散与慧差，其形式如图3所示。

图2 同轴子孔径检测误差 Fig.2 Testing error of coaxial sub-aperture

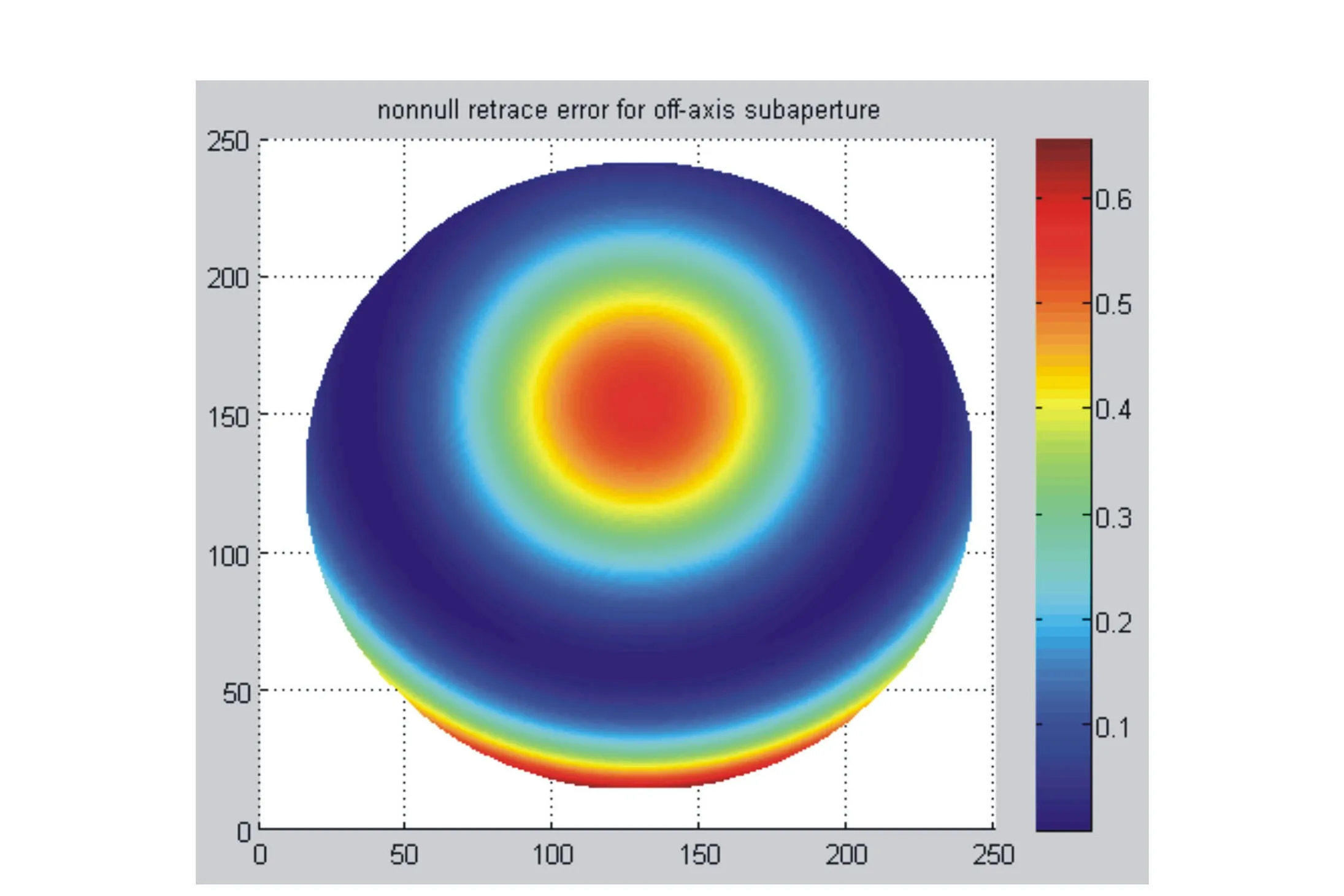
图3 离轴子孔径检测误差 Fig.3 Testing error of off-axis sub-aperture

在对各子孔径进行非零位检测误差剔除后，即可将各子孔径数据进行拼接计算。

假设将检测子孔径数目为N，其中第N个子孔径为基准子孔径，第i个子孔径的相位值可以表示为：

(1)

式中，Φi(x,y)为子孔径i的检测结果，fk(x,y)为调整项形式，L为定义好的调整项系数，对于非球面镜检测，其形式如式(2)所示[15]：

(2)

在求解拼接系数时，使目标函数达到最小值，即：

(3)

式(3)可以写为线性方程组形式：

P=Q·R,

(4)

其中

(1)P是一个(N-1)×L行的向量，用P(j-1)k代表第((j-1)·L+k)行元素，j为子孔径序号，k为拼接系数所对应方程序号，则

[Φj(x,y)-Φi(x,y)] ,

(5)

(2)Q是(N-1)×L阶矩阵，同理用Q[(j-1)k][(l-1)k′]代表第[(j-1)·L+k]行，第[(l-1)·L+k′]列元素，l为子孔径的序号，k′为拼接系数对应方程序号，则

Q[(j-1)k][(l-1)k′]=

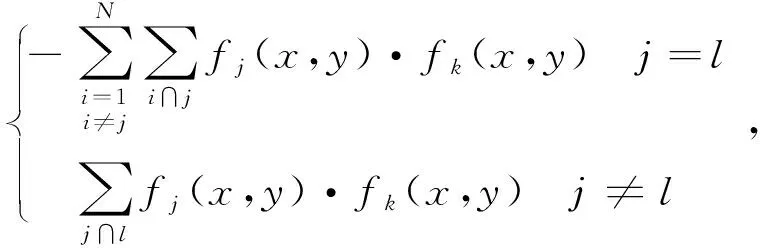
(6)

(3)R为一个(N-1)×L行的向量，同理用R(j-1)k代表第((j-1)·L+k)行元素，则

R(j-1)k=ajk,

(7)

式中，ajk是对应于第j个子孔径方程fk(x,y)的拼接系数。

3 实验验证

为了验证上述拼接算法的可行性，本文对一口径为130 mm的凸双曲面镜进行了拼接检测，其中镜面参数如下：二次曲面常数k为-1.812 8，顶点曲率半径为1 227.65 mm。

检测中使用口径为150 mm，F数为11的球面标准镜，子孔径检测半径：

(8)

检测光路如图4所示。

图4 检测装置图 Fig.4 Experimental setup

检测中，对被检测镜规划了5个检测子孔径，其中子孔径规划路径如图5所示。检测中，利用激光跟踪仪对检测光路进行几何量测量，以保证非球面镜与干涉仪位置的正确性，从而保障子孔径检测时调整误差与加工误差的有效分离。

图5 子孔径规划示意图 Fig.5 Schematic diagram of sub-aperture arrangement

图6 子孔径检测结果 Fig.6 Test results of sub-apertures

各子孔径检测结果如图6所示。各子孔径通过标记点确定相对位置，对于中心子孔径，其非零位检测误差如图7所示，对于离轴子孔径，其非零位检测误差如图8所示。在对各子孔径进行非零位检测误差剔除后，全口径拼接结果如图9所示。

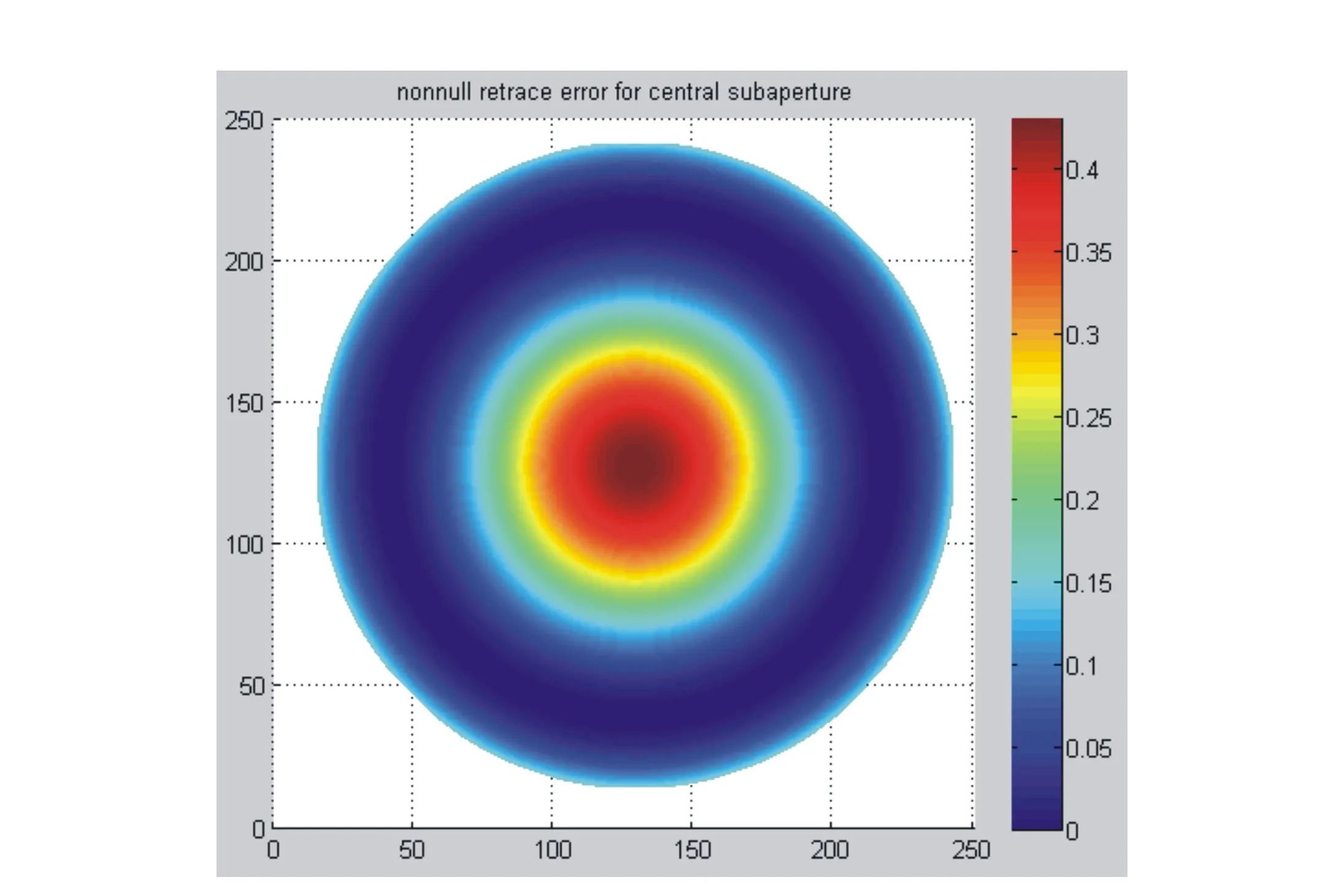
图7 中心子孔径非零位检测误差 Fig.7 Non-null retrace error of central sub-aperture(pv 0.431λ rms 0.116λ)

为了评价拼接精度，通常将拼接结果与全口径检测结果进行对比。然而实际检测中，之所以进行拼接检测，通常是由于无法对其直接进行全口径检测。

为了在无法直接获得全口径检测结果的情况下对拼接精度进行评价，本文采取自检验评价法[16]。

其中自检验子孔径检测结果如图10所示，拼接结果与自检验子孔径检测结果的残差图如图11所示。残差的PV与RMS值分别为0.016λ与0.003λ，验证了拼接检测的精度。

图8 离轴子孔径非零位检测误差 Fig.8 Non-null retrace error of off-axis sub-aperture(pv 0.656λ rms 0.169λ)

图9 子孔径拼接结果 Fig.9 Stitching map of sub-aperture

图10 自检验子孔径检测结果 Fig.10 Testing map of self-examine sub-aperture

图11 残差图 Fig.11 Residual map

4 结 论

本文对凸非球面镜拼接检测技术进行了研究，该方法可以有效拓宽干涉仪测试的动态范围，无需其它辅助光学元件就能够实现对凸非球面的测量，这不仅提高了分辨率，降低了成本，而且缩

短了工期。同时结合工程实例，对一口径为130 mm的凸非球面进行了非零位拼接检测，并基于自检验的评价方式评价拼接精度，全口径拼接结果与自检验子孔径结果的残差图PV与RMS分别为0.016λ与0.003λ，验证了本文拼接算法的可信性与精度。