步进电机驱动的直线变倍成像系统研究

李 铮，戴 明，李嘉全

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033;2.中国科学院大学，北京 100049)

1 引 言

目前，直线变倍成像系统以其变焦范围大、拍摄稳定等优点，被广泛应用于航天航空、军事工业、光电侦查等领域。采用电机驱动代替凸轮驱动实现变焦是国内外该领域的主要研究方向之一。电机驱动可以有效解决传统凸轮曲线加工精度要求高、装配调试难度大和易发生不可逆机械磨损等问题。尤其是电机驱动控制技术的不断发展，使这种驱动方式的优越性愈来愈显著。

随着计算机技术和微电子技术的发展，电机领域研究的不断深入，步进电机的定位精度、响应速度和稳定性等性能进一步提高。目前国内外这方面的研究主要集中于研究符合步进电机矩频特性的加减速控制曲线。而基于数字图像处理技术的图像清晰度评价方法因具有区分度高、判断准确且快速高效等优点受到广泛青睐。基于空间域、频率域和小波域的评价函数多种多样，各具特点[1]。此外，自动聚焦算法也多种多样，例如：斐波那契查搜索算法、扫描反馈搜索算法、焦点检测法、穷举搜索算法以及盲人爬山搜索算法等[2]。目前使用中通常是基于系统特点和适用性要求，对常用算法进行升级和优化。

直线变倍成像系统主要功能的实现包括两个过程，即变焦过程与聚焦过程。在变焦过程中，通过移动活动组透镜的位置来实现系统输出焦距值的改变。而聚焦过程用于补偿前者造成的像面漂移。像面补偿方式有光学补偿法和机械补偿法两种，目前广泛采用机械补偿法[3-5]。

本文在双二相混合式步进电机驱动的机械补偿式连续变焦系统的基础上，将步进电机的速度控制模型运用到变焦算法中，并采用反馈扫描搜索算法和基于图像梯度算子的清晰度评价函数来完成镜头的标定和变焦算法的设计。采用DSP和FPGA结合的图像处理单元，驱动芯片控制步进电机的运行方式实现系统的硬件平台。最后，从步进电机定位精度与系统变焦精度、光学性能和外场拍摄性能3个方面对系统进行测试。

2 直线变倍成像系统介绍

直线变倍成像系统主要由成像模块、图像传感模块、图像处理模块和变焦驱动模块组成，下面将简单介绍这4部分。

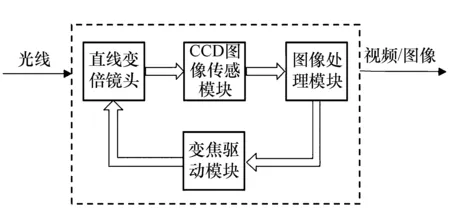
图1 直线变倍成像系统的构成 Fig.1 Composition of continuous zooming system

2.1 系统各功能模块介绍

本文采用机械补偿式连续变焦镜头[6]。变焦原理如图2所示。

图2 直线变倍镜头的变焦原理 Fig.2 Zoom principle of continuous zooming lens

镜头的光学部分主要由4组镜头组成：前固定组、变倍组、补偿组和后固定组[7-8]。4组镜头的具体作用如下：

(1)前固定组：为系统提供固定的像。

(2)变倍组：在变焦过程中多作线性运动，承担系统的变倍(焦距)作用。

(3)补偿组：按特定规律的曲线轨迹作非线性运动，以补偿在变倍过程中变倍组镜头移动所产生的像面漂移，起稳定像面的作用。

(4)后固定组：将补偿组镜头的像转化为最终实像，调整整个变焦系统的合成焦距值、设备孔径光阑，保证在变焦过程中系统的相对孔径不变，并补偿其余3组透镜的像差[9]。

系统变焦时，变倍组透镜沿着光轴按照图中虚线移动，移动过程中，系统的合成焦距值发生改变，同时像面也会发生移动。此时，补偿组透镜沿着光轴按照图中虚线移动，以补偿变焦造成的像面漂移，使整个系统的像面保持稳定，从而使系统输出清晰稳定的像。

图3 变焦机构示意图 Fig.3 Structure diagram of zooming mechanism

图像传感模块的作用是把直线变倍镜头输出的信号进行光—电转换，然后经放大与模数转换电路转换后输出数字图像信号，用于数字图像处理模块的进一步处理。图像处理模块的作用是预处理图像数据、协调通信、图像目标追踪以及自动聚焦策略。

2.2 系统硬件平台的搭建

本文选用的直线变倍镜头的范围为50～500 mm，变焦和聚焦结构均为步进电机+丝杠；选用AD-080CL型CCD逐行扫描相机；图像处理和驱动控制模块由TMS320F28335DSP和FPGA组成；选用28BYG3401型二相混合式步进电机，步距精度为0.02 mm；为了满足质量和体积要求，采用THB6064AH型驱动芯片代替专门的驱动器，最高可实现64细分；选用C8051F336单片机作为微处理器。

3 直线变倍成像系统的算法设计

3.1 步进电机的加减速曲线

步进电机的矩频特性曲线如图4所示，虚线表示电机实际的矩频特性。可见，当驱动脉冲频率较低时，电机转矩较大；当驱动脉冲频率升高时，电机转矩成线性下降。

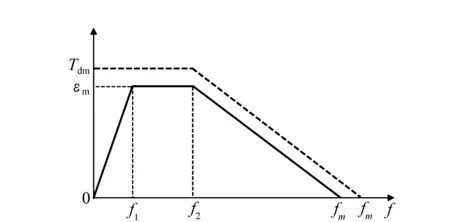
图4 步进电机矩频特性及角加速度曲线 Fig.4 Torque-frequency characteristics and the curves of angular acceleration for stepping motor

当电机平稳运转时，转子的角加速度ε跟脉冲频率f对时间t的微分成正比。如图4中实线所示角加速度ε与脉冲频率f的关系，3段直线都可以表示为一次方程：

(1)

式中：A、B为待定常数。

对式(1)进行拉普拉斯变换、反拉普拉斯变换，并进行整理得：

(2)

式中：C=Aτ-f0；τ=1/B为时间常数。

根据式(2)可以得到与步进电机矩频特性变化规律相对应的加速曲线。

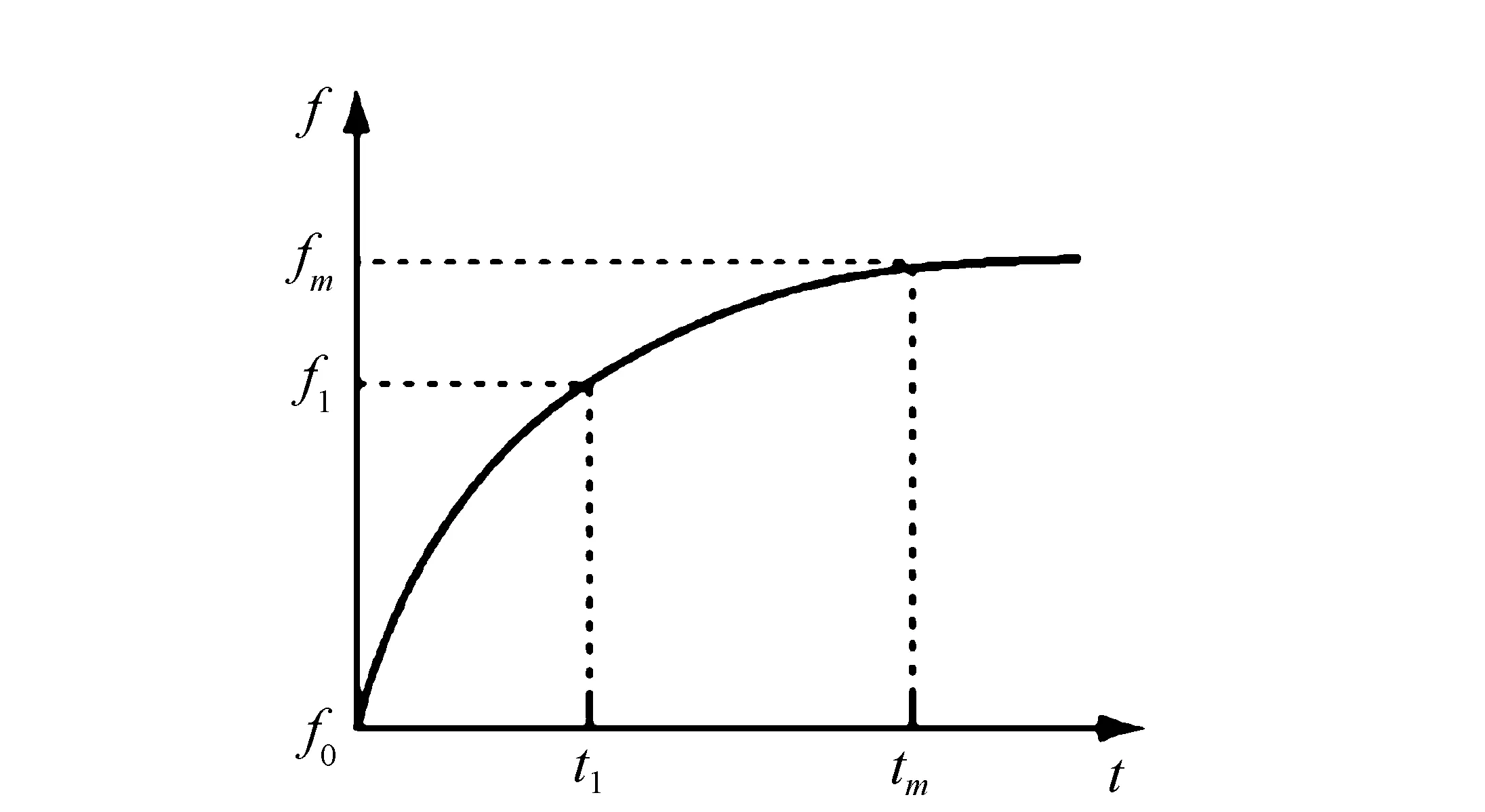
图5 步进电机加速曲线 Fig.5 Acceleration curve of stepping motor

对曲线进行离散化处理，设某一时刻t时，输出第n个驱动脉冲，设N为电机加速时钟脉冲序列，则第n个脉冲的频率可以简化为：

f(n)≈f0+fm(1-e-n/g) ,

(3)

式中：g表示经过脉冲序列N后频率增加的快慢程度。

利用单片机定时中断方式控制I/O口输出电平，每两次中断产生1个周期脉冲T(n)，不断改变定时器的装载值，用离散的办法逼近理想的速度变化曲线。将各个速度离散点所对应定时器装载值提前载入ROM[10]。定时器的装载值K(n)可以通过f(n)转化而来：

(4)

采用16细分驱动，步距角为0.112 5°。设f0=60 Hz，fm=12 000 Hz，N=80，g=50，单片机晶振频率为12 MHz。可以得到K(n)数据表。减速过程曲线与加速过程对称，逆向调用即可。

3.2 聚焦评价函数的构造

本文采用基于空间域图像灰度算子来构造一个简单易行、性能稳定的聚焦评价函数[11-12]。

选取两张标准图片，分别对应于系统短焦和长焦范围的拍摄情况。利用离焦函数以10、15、30的半径进行离焦处理，来模拟镜头的离焦情况[13-14]。

图6 离焦化处理的复杂背景图片 Fig.6 Complex background images after defocusing process

分别计算这组图像的几种评价函数值，并将结果归一化处理，绘制成折线图，如图7所示。

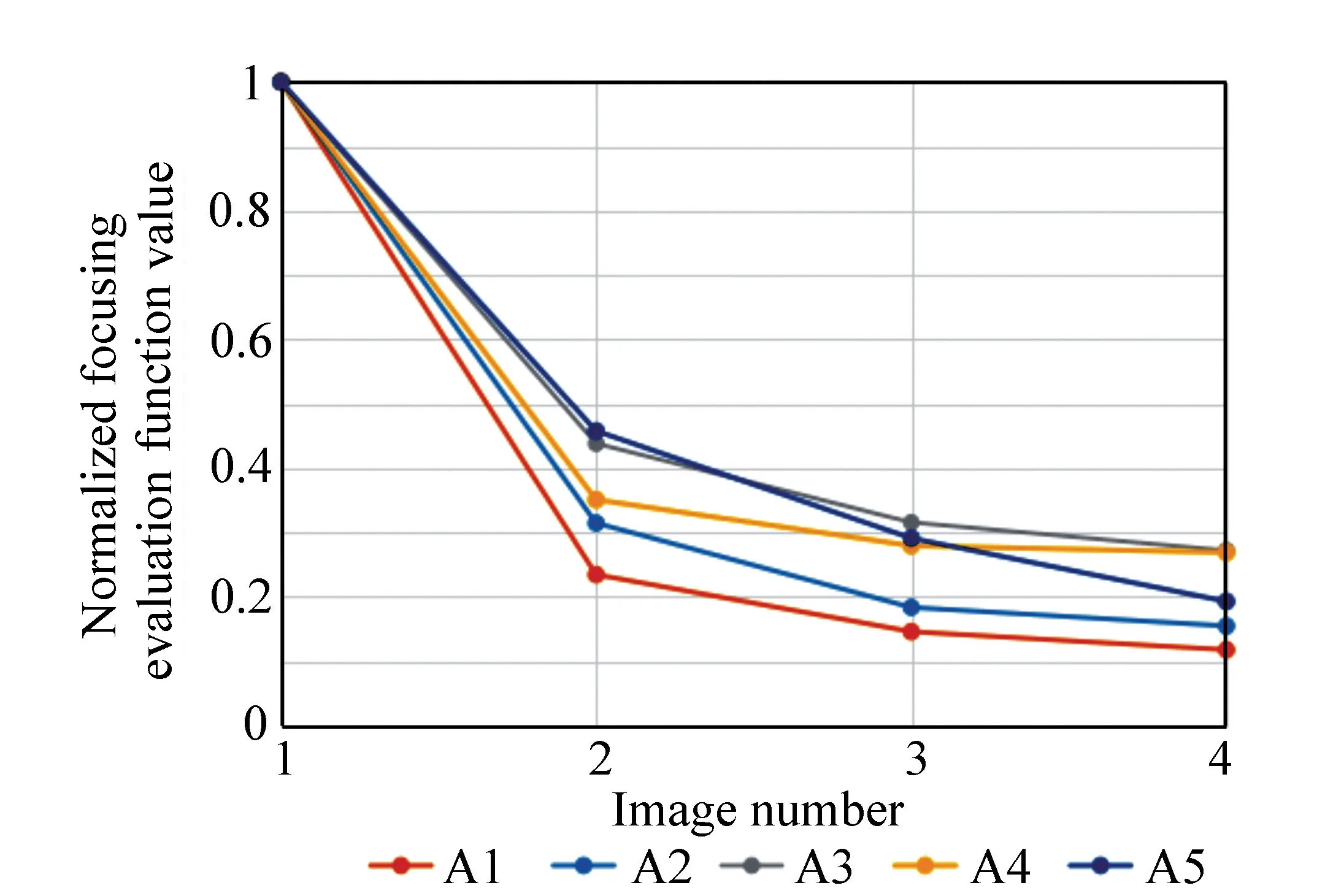
图7 复杂背景各评价函数值折线图 Fig.7 Chart of evaluation function values for complex background image

图中：横坐标“1”“2”“3”“4”分别代表图7(a)(b)(c)(d)；其中，A1为灰度梯度模方和函数；A2为Roberts梯度模方和函数；A3为Prewitt梯度模方和函数；A4为Tenengrad函数；A5为Brenner函数。

图8 离焦化处理的简单背景图片 Fig.8 Simple background images after defocusing

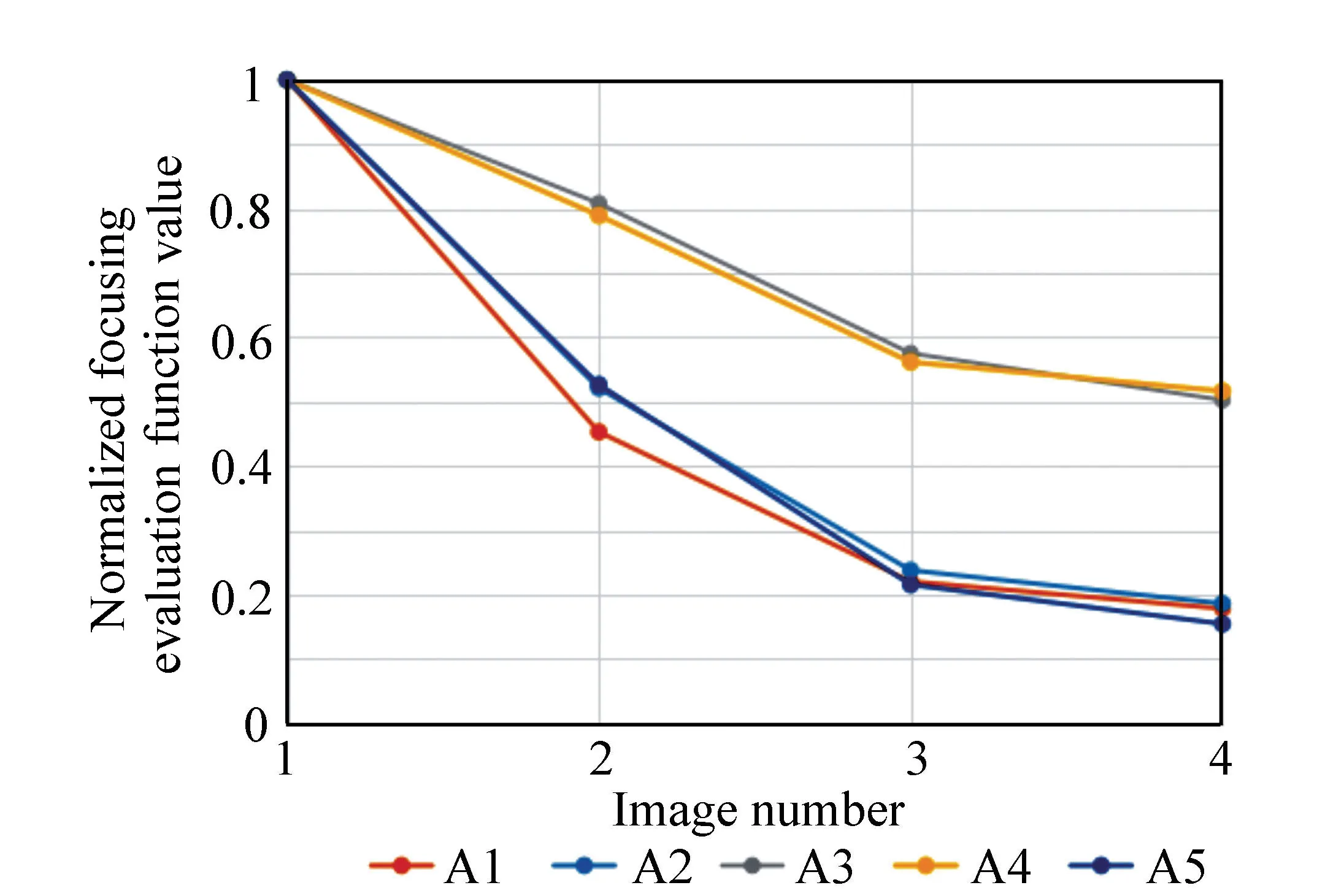
图9 简单背景各评价函数值折线图 Fig.9 Chart of evaluation function values for simple background image

对简单背景与复杂图像作相同处理得到图8、图9。分析图7和图9，可以发现以下规律：

(1)离焦函数半径越大，即离焦情况越严重，评价函数值越低，准确聚焦位置函数值达到最大。

(2)灰度梯度模方和函数与Roberts梯度模方和函数对于离焦程度比其他函数更为敏感。当离焦发生时，其函数值下降趋势较明显，曲线陡峭。

(3)随着离焦函数半径的增大，复杂背景图像与简单背景图像的变化趋势更加明显。

综上，选择灰度梯度模方和函数与Roberts梯度模方和函数的平均值作为聚焦评价函数。

Gx1=[f(x,y+1)-f(x,y)]

Gy1=[f(x+1,y)-f(x,y)]

Gx2=[f(x+1,y+1)-f(x,y)]

Gy2=[f(x+1,y)-f(x,y+1)] ,

(5)

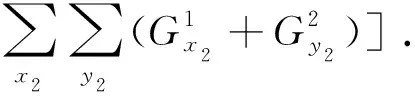
(6)

根据式(5)和(6)计算上述两组图像的聚焦评价函数值，并绘制折线图，如图10所示。

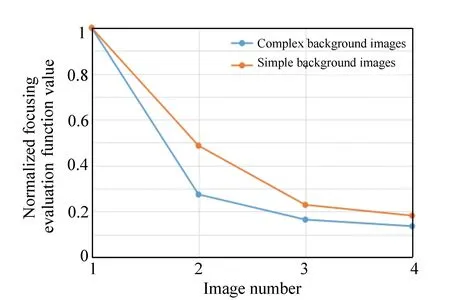
图10 归一化聚焦评价函数值的折线图 Fig.10 Normalized evaluation function value

通过分析归一化的聚焦评价函数折线图，可以发现它具备以下优点：

(1)满足聚焦评价函数的各项要求，如单峰型、无偏性、易于实现等。

(2)随着离焦函数半径的增大，图像的评价函数值迅速降低，说明该函数对图像的离焦程度敏感。

(3)对于复杂背景图像和简单背景图像的评价结果差别不大，满足变焦系统焦距连续变化的要求。

(4)函数是基于空间域梯度算子实现的，运算简单，实时性较好。

3.3 系统的变焦算法

离线标定可以预先得到移动组镜头位移与焦距的对应关系，变焦时直接读取数据，简化算法，节省存储空间，从而提高系统的响应速度和效率[15-16]。

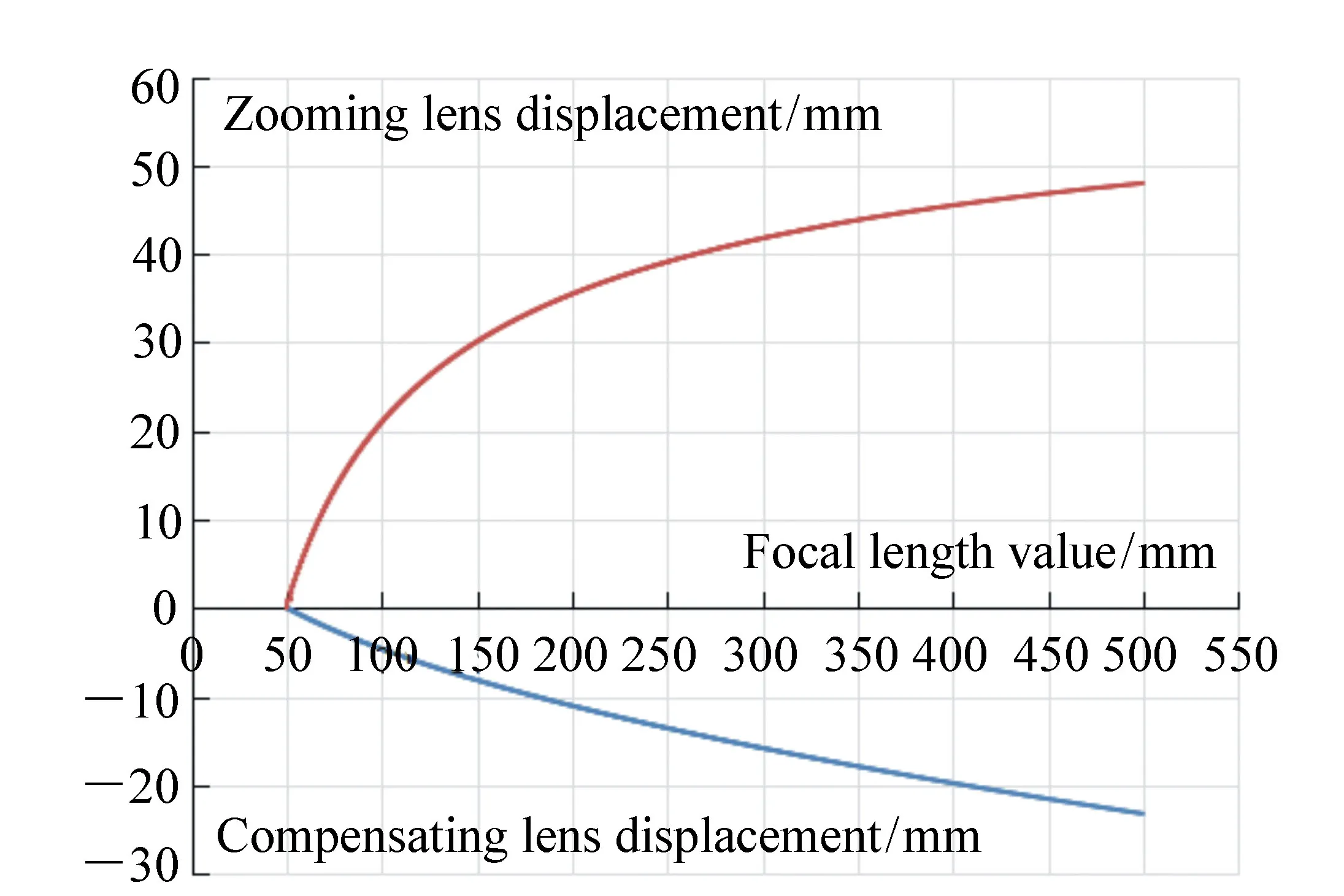
图11 变倍组、补偿组位移与焦距值对应关系曲线 Fig.11 Relation curves of the displacements of zooming lens, compensating lens and the focal lengths

通过标定实验得到的移动组镜头位移与焦距值之间一一对应的数值关系。如图11所示。

将位移数据进行曲线拟合，从而得到变焦距控制方程。如式(7)所示，最高次项为x6，拟合误差SSE为0.034 11，在允许范围内。

y=-0.010 65-0.148x-0.005 153x2+

0.000 279x3-1.545×10-5x4+

3.443×10-7x5-3.334×10-9x6.

(7)

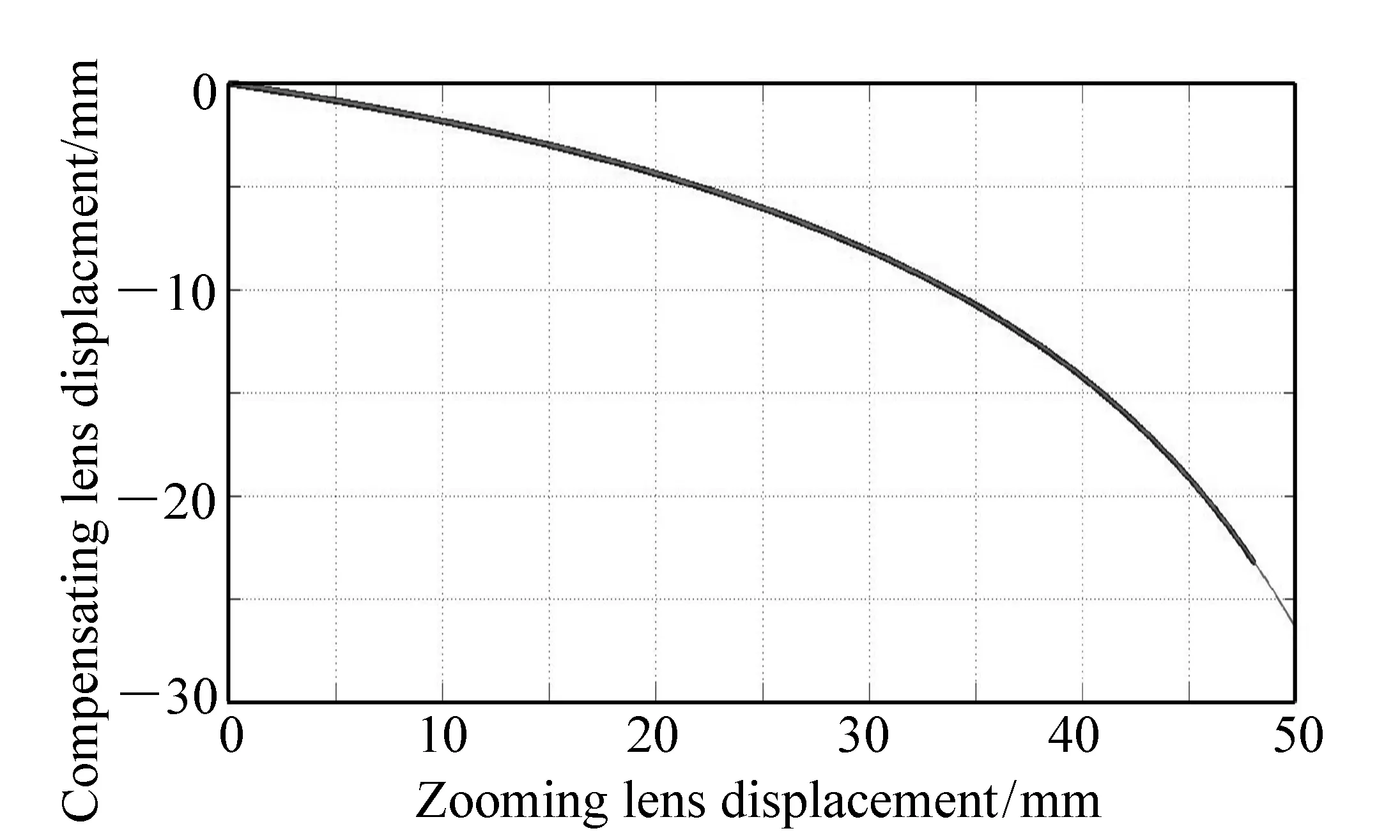
图12 变倍组与补偿组位移关系曲线 Fig.12 Relation curve of displacements of zooming lens and compensating lens

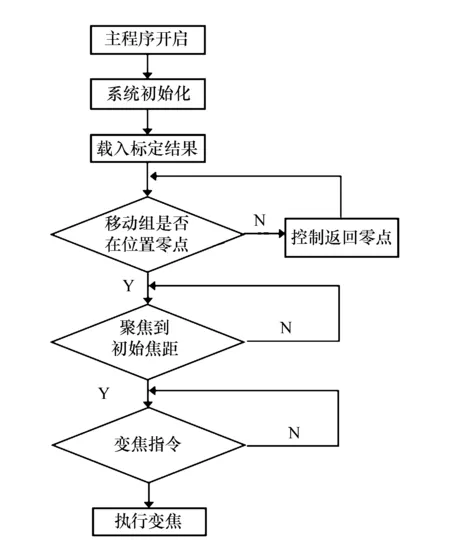
图13 直线变倍成像系统变焦流程图 Fig.13 Zooming flow chart of zooming imaging system

系统的变焦控制流图如图13所示。

4 系统的性能测试及实验分析

4.1 系统的变焦精度

移动组透镜最大位移范围为50 mm。采用和不采用速度控制模型的情况下，分别计算5 mm、10 mm、15 mm、…、50 mm各点的定位误差，如图14所示。图中，曲线1表示未采用速度控制模型的情况，曲线2表示采用速度控制模型的情况。

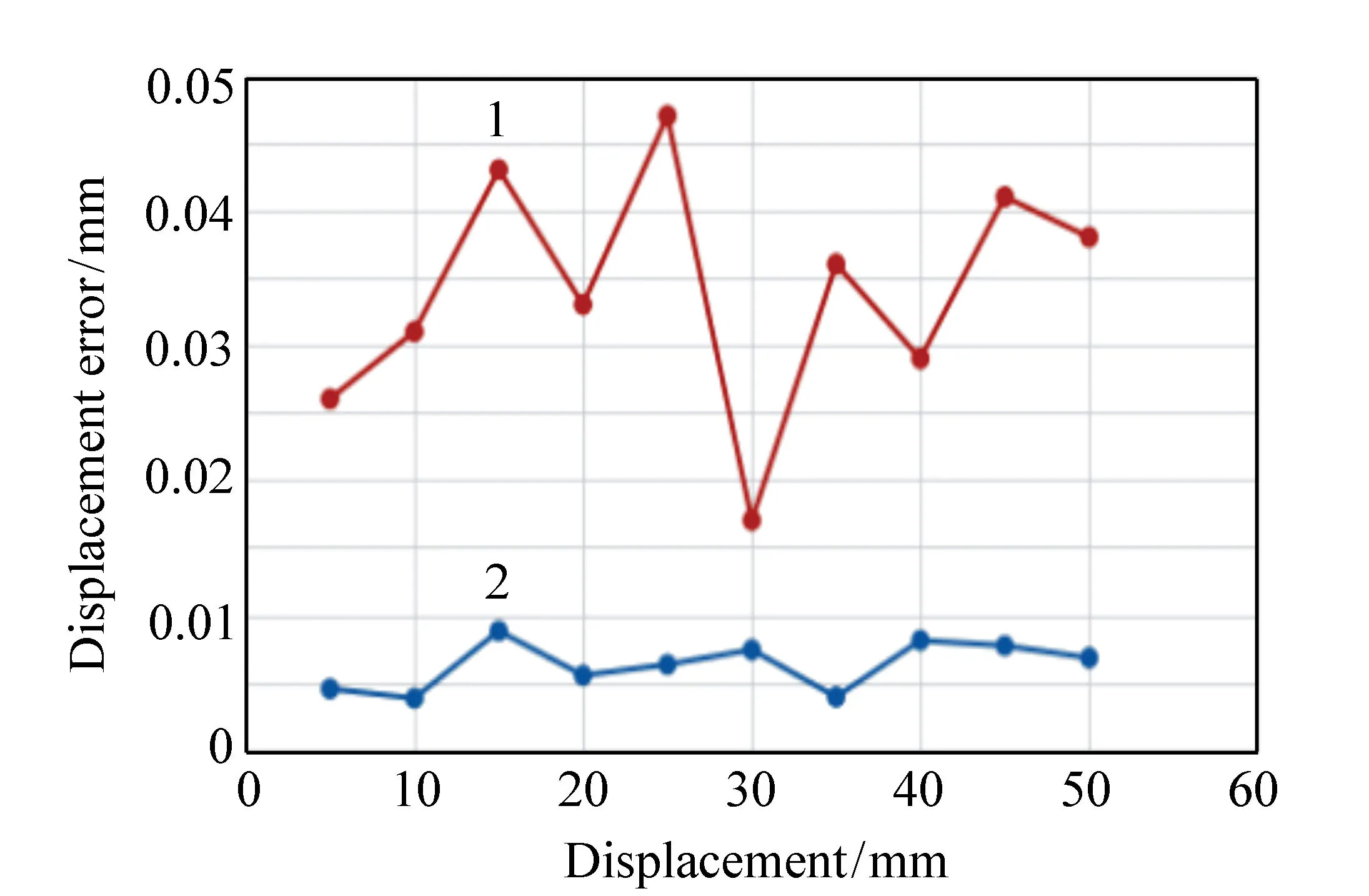
图14 步进电机位移误差 Fig.14 Displacement error of stepping motor

如图14所示，在未采用速度控制时，定位误差在0.015～0.050 mm内。而采用速度控制后，定位误差明显降低，在0.010 mm以下。且前者误差波动较大，后者的误差相对平稳。

从50 mm连续变焦到500 mm的过程中，选取16个点处焦距的标定值与实测值，来计算镜头的变焦精度。

根据表中的数据，系统定位随机误差为：

变焦精度是指定位随机误差与当前焦距值的比值，计算得到镜头在当前焦距下的变焦精度约为0.15%，远小于1%。

表1 焦距标定值与实测值结果Tab.1 Focal length calibration values and measured values

4.2 系统的光学性能

4.2.1 光学传递函数[17-18]

本系统光学传递函数的特征频率为108 lp/mm，波长f为486.12 nm～546.07 nm～656.27 nm，权重为1∶2∶1。利用ZEMAX得到镜头不同焦距下的MTF曲线如图15所示。

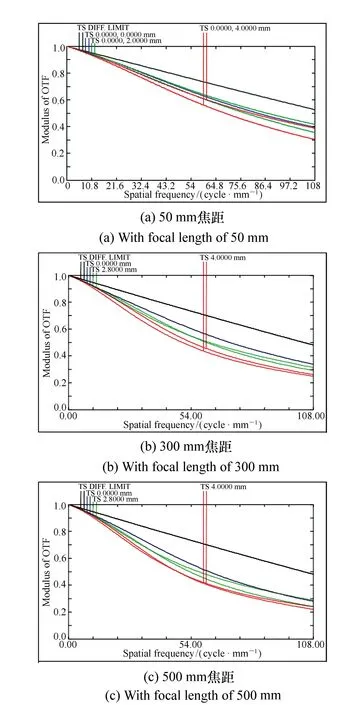
图15 不同焦距下的MTF曲线 Fig.15 MTF curves under different focal lengths

分析镜头不同焦距下的MTF曲线可以发现，3组曲线的MTF值接近1，即线性度较高，反差和分辨率良好。曲线平坦，表明镜头边缘和中心的成像差距较小。每组曲线变化趋势一致且较为接近，表明镜头的焦外成像性能良好。

4.2.2 畸变

利用ZEMAX得到直线变倍镜头不同焦距下的畸变曲线如图16所示。

分析镜头在不同焦距下的畸变曲线可以看出：50 mm短焦、300 mm中焦和500 mm长焦情况下，全视场范围内畸变均控制在0.5%以下，表明镜头的相对畸变较小，成像质量较高，满足系统的要求。

4.3 系统外场拍摄性能

本文的直线变倍成像系统的焦距值为50～500 mm，分别在50 mm短焦距、300 mm中焦距和500 mm长焦距状态下，连续拍摄欠焦、聚焦、过焦图像，如图17～图19所示。图20为不同焦距下所拍摄图像的归一化评价函数。

由图20可见，在焦点位置成像最为清晰，距离焦点越远，图像越模糊。分别计算3种焦距下各组图像的聚焦评价函数值，最后把函数值绘制成折线图。

50 mm焦距情况下，函数值随着离焦程度的递增显著下降；300 mm焦距情况下，这种下降趋势明显变缓；500 mm焦距情况下，函数值下降趋势最缓。各组图像的评价函数值的变化趋势基本一致，均在准确聚焦位置达到最大值，表明系统聚焦性能良好。

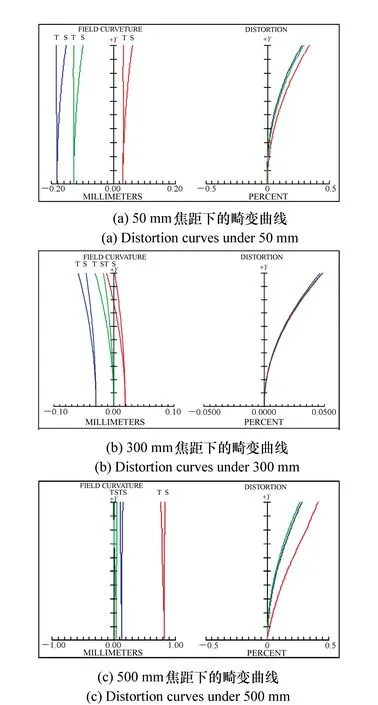
图16 镜头不同焦距下的畸变曲线 Fig.16 Distortion curves under different focal lengths

图17 50 mm焦距焦点附近连续拍摄图像 Fig.17 Continuous imaging results in the area near focus under 50-mm focal length

图18 300 mm焦距焦点附近连续拍摄图像 Fig.18 Continuous imaging results in the area near focus under 300 mm focal length

图19 500 mm焦距焦点附近连续拍摄图像 Fig.19 Continuous imaging near 500 mm focal length

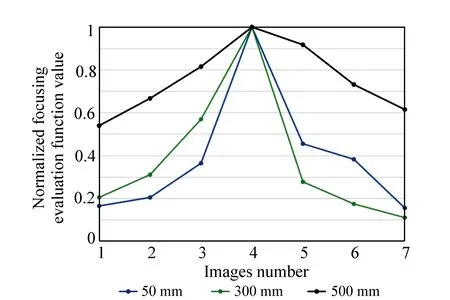
图20 不同焦距下拍摄图像的归一化评价函数值 Fig.20 Normalized evaluation function values of the images under different focal lengths

5 结 论

本文在无人机光电载荷的项目背景下，研究了采用双二相混合式步进电机驱动的机械补偿式连续变焦系统。从系统工作原理着手，分析各功能模块的作用和构成，搭建硬件平台。根据步进电机运行时的矩频特性设计合理的加减速控制曲线，并利用单片机控制步进电机的加减速过程。通过数字图像处理的方式，分析各个基于空间域图像梯度算子的清晰度评价函数，并构造了性能良好适用于本系统的聚焦评价函数。然后，采用扫描反馈搜索算法对直线变倍镜头的焦距值进行标定，并将标定曲线载入系统变焦算法。最后，对系统的变焦精度、光学性能以及外场拍摄性能进行测试。

实验结果表明，采用加减速控制的步进电机的定位精度大大提高，定位误差控制在0.010 mm以内。系统的变焦定位随机误差约为0.73 mm，变焦精度远小于1%。而且，光学性能和外场拍摄性能良好，而且体积小、重量轻，完全满足无人机光电载荷的适用性要求。