不同类型降雨条件下含裂隙土质边坡渗流特性分析

魏凌傲 王正君 郜 迪

(黑龙江大学 水利电力学院， 哈尔滨 150080)

降雨对边坡的稳定性影响巨大，主要体现在：降雨抬高了地下水位，使得土体的有效应力减小[1-2]；降雨使得边坡内部土体的强度减小，土体更容易发生剪切滑动[3-4]．同时，也有研究表明，不同类型降雨对边坡的渗流特性影响巨大：如郁舒阳[5]对不同类型降雨下的不同Fredlund&Xing参数土体的渗流特性进行了研究；王宁伟[6]对在不同类型降雨条件下的边坡入渗深度以及体积含水量变化规律进行了探讨．

在自然的风化作用以及草本植物根系作用下，边坡土体表层难免会产生一定角度，一定深度的裂隙[7]，这些裂隙的渗透性较原状土更高，可以极大的改变降雨过程中的雨水入渗规律，已有学者对其进行了相应的研究：如袁俊平[8-9]系统的对降雨条件下膨胀土裂隙的分布位置，各向异性程度，裂隙角度以及裂隙深度的渗流特性进行了分析；王培清[10]对裂隙性红黏土降雨条件下的边坡渗透稳定性进行了研究；阙云[11]对降雨条件下的裂隙性粘土边坡的渗流特性进行了模拟讨论，但是纵观国内外文献，不同降雨类型下含裂隙边坡渗流特性却鲜有报道，相应的规律还没有一个清晰的认识．

本文以某含裂隙土质边坡模型为例，选取平均型，前锋型，中锋型以及后峰型4种降雨类型，利用有限元分析软件Geo-slope中的Seep/w与Slope/w模块，研究了不同类型降雨条件下裂隙不同深度，不同角度以及裂隙不同渗透比的渗流特性，所得结果为进一步认识不同类型降雨下含裂隙边坡的渗流特性以及治理提供了一定的参考．

1 计算理论与模型

1.1 计算理论

非饱和渗流的控制方程形式为：

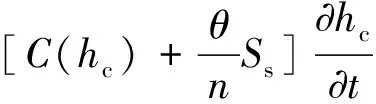
(1)

式中，kr为相对透水率；kij为饱和渗透张量；hc为压力水头；Q为源汇；C(hc)为容水度；θ为压力水头函数；n为孔隙率；Ss为单位贮水量．

土水特征曲线是描述土体渗透系数或者体积含水量与基质吸力的关系，采用VG模型进行估算[12]：

(2)

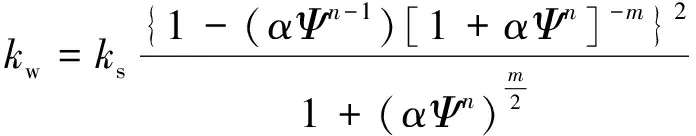
(3)

式中，θw为土体的含水率；θs为土体的饱和含水率；θr为土体的残余含水率；ks为土体的饱和渗透系数；kw为土体的瞬时渗透系数，即相应基质吸力下对应的渗透系数；Ψ为土体的基质吸力；a，m，n为公式的拟合参数，其中n可以表示为：

n=1/(1-m)

(4)

1.2 计算模型及边界条件

模型取自文献[9]，边坡的坡高为10 m，坡比为1∶2，裂隙位置设置在坡顶，如图1所示．在裂隙位置设置一监测面来实时监测不同类型降雨过程中的孔压以及体积含水量的变化规律．模型网格剖分图如图2所示，在坡顶裂隙处网格适当加密，全局一共剖分为755个单元，801个节点．

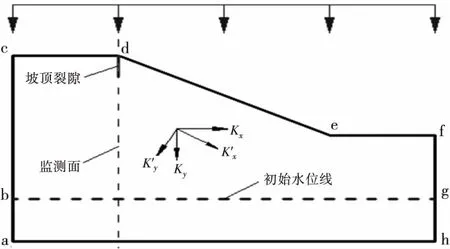
图1 计算模型

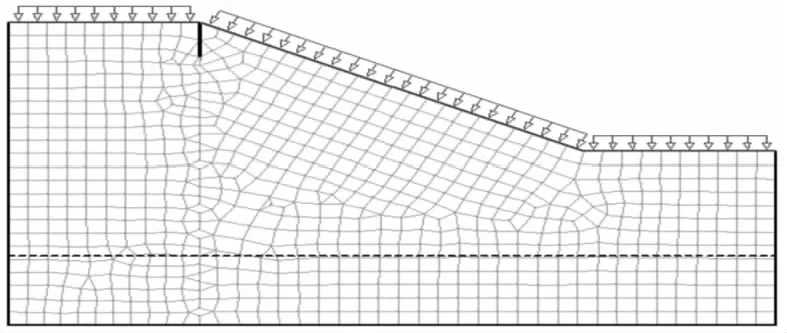
图2 模型网格剖分图

模型初始条件取如图1所示的初始水位下的渗流场作为整个计算工况的初始渗流场，边界条件如下：ab，gh为零流量边界；ah，bc，fg为不透水边界；cdef为降雨入渗边界．

裂隙模拟方法较多，本文取文献[8]的模拟思路，即将裂隙土部分视为一种各向异性材料，而在计算过程中，裂隙的数学描述可以用裂隙长度h，即裂隙沿着深度方向的长度大小；裂隙面与竖直方向的夹角α，以及顺裂隙方向与垂直裂隙方向的渗透系数比值μ来刻画．其中，裂隙单元的局部坐标与整体坐标的转换关系如下式所示：

(5)

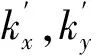
2 计算方案及材料参数

降雨采用4种不同类型降雨，平均型，前锋型，中锋型以及后峰型降雨，降雨过程曲线如图3所示，降雨总量为0.14 m，降雨天数为7 d，同时考虑停雨5 d的情况，总计算时间为12 d．

图3 降雨过程曲线

计算内容考虑裂隙不同深度，不同裂隙方位角α以及不同的渗透系数比值μ(即顺裂隙方向与垂直裂隙方向渗透系数比值)在不同类型降雨条件下的渗流特性，具体计算工况见表1．

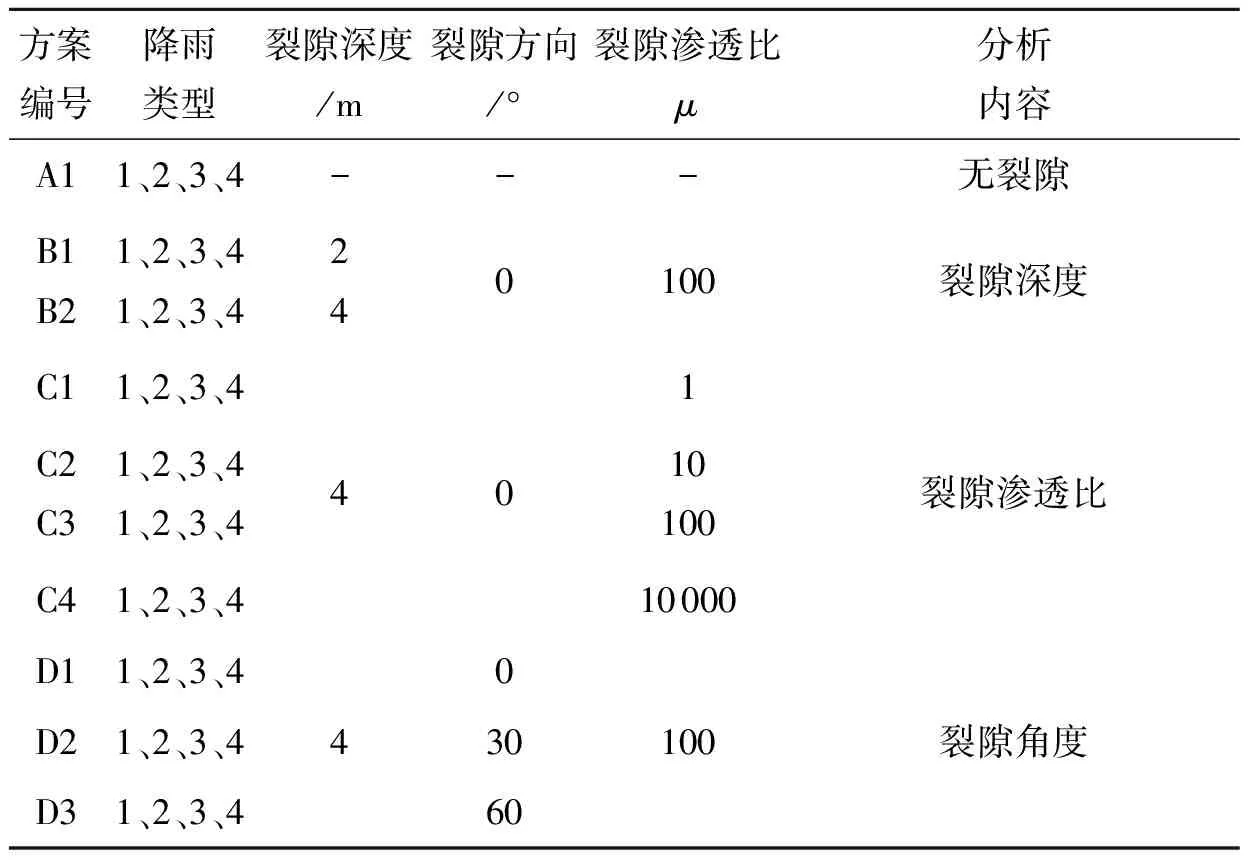
表1 计算工况

注：降雨类型1、2、3、4分别代表平均型降雨，前锋型降雨，中锋型降雨以及后峰型降雨．

土体渗流参数依据文献[9]确定，a=166.7 kPa，n=1.567，θs=0.495，θr=0.262，原状土饱和渗透系数ksat=2.83×10-4m/d，垂直裂隙方向饱和渗透系数ksatx=2.83×10-2m/d，根据公式(2)～(4)，可以得出原状土与裂隙土的土水特征曲线如图4所示．

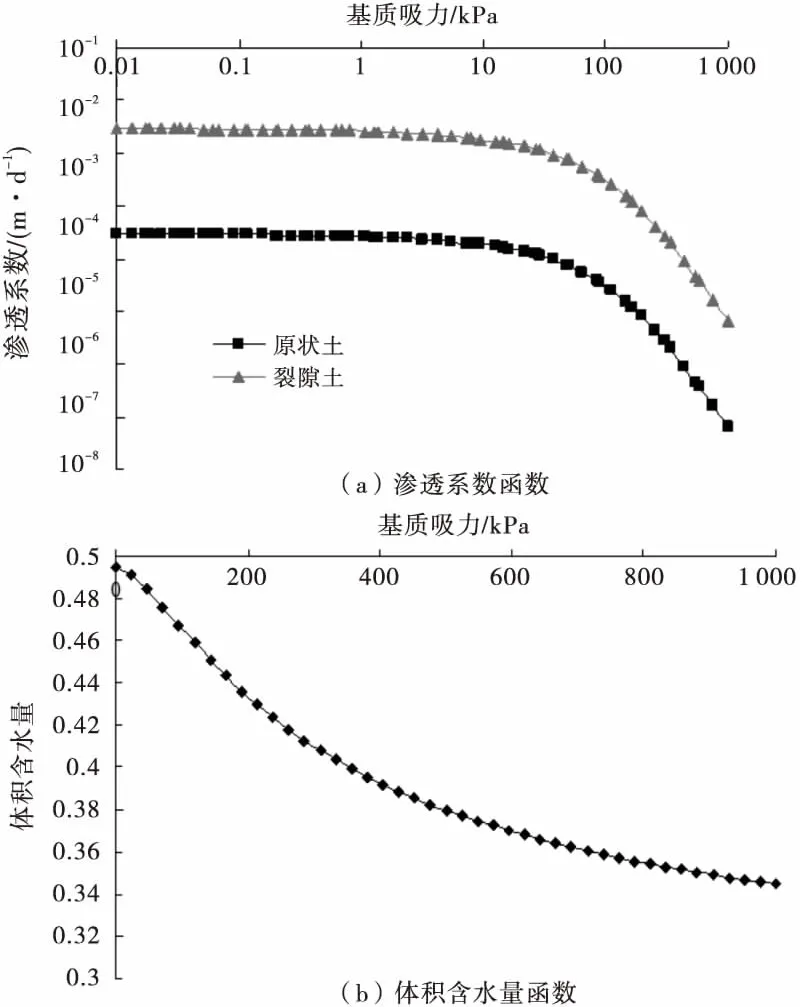
图4 土水特征曲线

3 计算结果分析

3.1 不同裂隙深度渗流特性

边坡无裂隙，坡顶裂隙深2 m以及坡顶裂隙深4 m情况下的监测面体积含水量变化如图5所示．

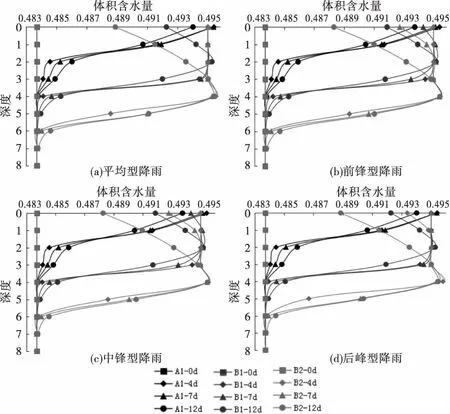
图5 工况A、B体积含水量变化

由图可见，不同降雨类型下，不同裂隙深度下监测面的体积含水量变化呈现不一样的规律，从整体上看，不同类型降雨工况下体积含水量变化存在一个“极限深度”，即湿润锋的最大影响深度，无裂隙工况下湿润锋影响的最大深度为4 m，裂隙为2 m工况下的湿润锋最大影响深度为6 m，而裂隙为4 m工况下的湿润锋最大影响深度为7 m，并且不同类型降雨对湿润锋的最大影响深度没有明显的影响；裂隙深度越深，在停雨后的土体表面体积含水量消散的越快，以图5(a)为例，无裂隙工况停雨后孔压消散最慢，在第12 d土体表层体积含水量为0.494，裂隙为2 m工况下的第12 d土体表层体积含水量为0.492，而裂隙为4 m工况下的第12 d土体表层体积含水量为0.489，因此，土体不含裂隙情况下体积含水量变化规律是随着深度逐渐递减，直到达到“极限深度”后保持不变，而含裂隙情况下体积含水量变化规律是随着深度先增大后减小，并且拐点约为裂隙深度处，最后减小到“极限深度”后保持不变；不同降雨类型对体积含水量变化规律影响不大，对每个瞬时的孔压数值大小稍有影响，以裂隙深度为4 m工况下不同类型降雨在第12 d的孔压为例，平均型降雨下土体表层孔压为0.489，前锋型降雨土体表层孔压为0.488，中锋型降雨土体表层孔压为0.488，而后峰型降雨土体表层孔压为0.489．相应的孔压变化规律如图6所示．

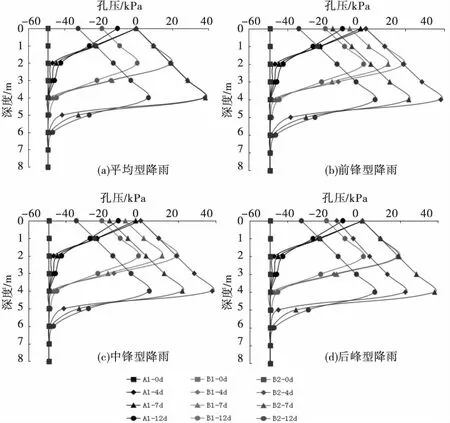
图6 工况A、B孔压变化

可见不同降雨条件下不同深度裂隙土体内部孔压变化规律较为一致，无裂隙土体在降雨过程中孔压呈现随深度逐渐减小的趋势，而含裂隙土体在降雨条件下孔压随时间呈现先增大后减小，最后保持不变的规律，且在裂隙底部孔压达到最大值，同时，裂隙深度越大，裂隙底部的最大孔压值也越大，以图6(a)平均型降雨为例，裂隙为2 m工况下所达到的最大孔压为20 kPa，而裂隙为4 m工况下所达到的最大孔压则为40 kPa,可见降雨过程中的最大孔压与裂隙深度呈正相关，纵向来看，不同类型的降雨只是影响了相应孔压达到最大的时间，对孔压的分布规律则影响较小．

3.2 不同裂隙渗透比的渗流特性

裂隙渗透比为1，10，100，10 000下的土体内部体积含水量变化规律如图7所示．

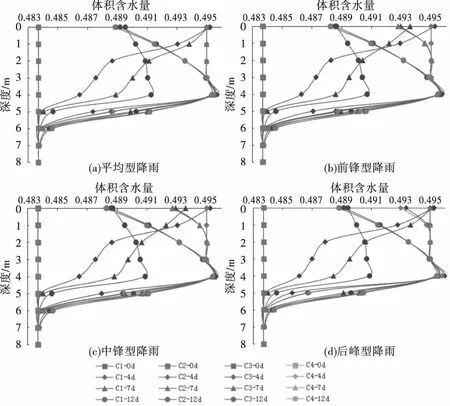
图7 工况C体积含水量变化

不同类型降雨条件下，不同渗透比呈现出明显的规律：即渗透比大于10体积含水量变化规律一致，而渗透比为1有明显的孔压滞后性，即土体表层的孔压消散较渗透比大的工况要慢，究其原因，是因为土体渗透比较大的情况下，垂直裂隙方向的渗透率就等于降雨的入渗强度，所以当渗透比大于10的工况下体积含水量变化规律趋于一致，而当渗透比较小时，降雨强度大于入渗强度，有一部分水被滞留于土体表层，即表现出体积含水量的消散“滞后”现象．不同类型降雨影响了不同时刻的体积含水量变化规律，以工况C1为例，平均型降雨下7 d土体表层一直保持为饱和状态，第12 d土体表层体积含水量减至0.489；前锋型降雨下在第7 d土体表层体积含水量就开始下降至0.4924，在第12 d时体积含水量降至0.487 8；中锋型降雨在第7 d土体表层体积含水量也有所下降，在第12 d降至0.4878；后峰型降雨条件下第7 d土体表面仍为饱和状态，而第12 d降至0.489 2．相应的孔压变化如图8所示．

图8 工况C孔压变化

孔压变化与体积含水量较为相似，即渗透比为1与渗透比大于10的孔压变化差异较大，这也是由于土体渗透比较大的情况下，垂直裂隙方向的渗透率就等于降雨的入渗强度，所以当渗透比大于10的工况下孔压变化规律趋于一致，而当渗透比较小时，降雨强度大于入渗强度，有一部分水被滞留于土体表层，即表现出孔压“滞后”现象；渗透比越大，土体内部达到的最大孔压也越大，同时，渗透比大于10孔压变化较为一致．

3.3 不同裂隙方位角渗流特性

裂隙方位角为0°，30°，60°情况下土体内部体积含水量变化规律如图9所示．

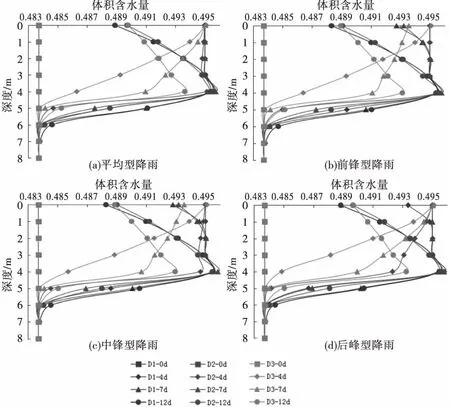
图9 工况D体积含水量变化

由图可见，在不同类型降雨条件下，裂隙方位角为0°与30°时体积含水量变化规律较为一致，而裂隙角度为60°情况下与前两种工况的差异性较大，这是因为裂隙方位角为0°与30°时，裂隙竖向渗透系数较大，雨水入渗较为容易，即两者体积含水量变化规律较为一致，而裂隙角度为60°时，裂隙接近于水平，而垂直裂隙方向的渗透系数较顺裂隙方向的渗透系数要小两个数量级，即雨水较难入渗，所以裂隙角度为60°时的体积含水量变化要滞后于0°与30°的体积含水量变化．不同类型降雨影响了不同时刻土体一定深度内的体积含水量变化，以工况D1为例，平均型降雨下7 d土体表层一直保持为饱和状态，第12 d土体表层体积含水量减至0.489；前锋型降雨下在第7 d土体表层体积含水量就开始下降至0.493，在第12 d时体积含水量降至0.488；中锋型降雨在第7 d土体表层体积含水量也有所下降，在第12 d降至0.488；后峰型降雨条件下第7 d体积含水量降至0.493 2，而第12 d降至0.487 9．相应的孔压变化规律如图10所示．

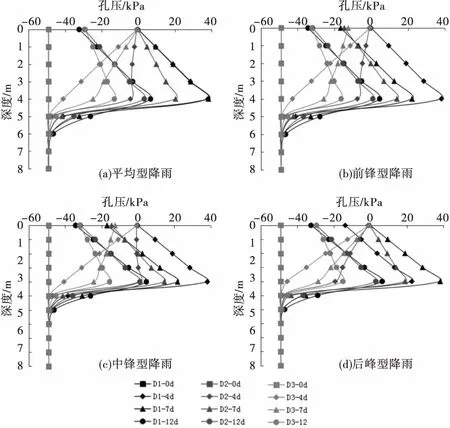
图10 工况D孔压变化

孔压变化与体积含水量变化有较好的吻合性，即裂隙倾角为0°与30°情况较为接近，而60°情况差异较大，这也是由于裂隙方位角为0°与30°时，裂隙竖向渗透系数较大，雨水入渗较为容易，即孔压变化较为一致，而当裂隙角度为60°时，裂隙接近于水平，而垂直裂隙方向的渗透系数较顺裂隙方向的渗透系数要小两个数量级，即雨水较难入渗，孔压变化较为缓慢，但是裂隙角度的差异性也比较明显，即随着裂隙角度的增大，土体表层孔压的消散速度也越来越慢，并且最大孔压也越来越小．不同类型的降雨也只是影响了相应孔压达到最大的时间，对孔压的分布规律则影响较小．

3.4 实例分析

文献[13]中介绍了南水北调南阳现场试验段膨胀土边坡滑坡破坏实例．现场调查结果表明，该现场试验段膨胀土裂隙极其发育，其中长大裂隙有至少2组以上优势方向，裂隙区域土体发现呈明显各向异性．裂隙倾向统计结果显示，主裂隙倾向与坡面几乎平行，即顺裂隙方向与竖向夹角约为50°～75°．现场观测表明，降雨后吸湿区范围约为0.5 m，吸湿区内土体含水率增大约为16.5%，表明这种裂隙倾向条件下，降雨入渗的影响范围和影响程度均较小．这与本文计算结果相吻合，即顺裂隙方向与竖直方向夹角较大时，裂隙各向异性对边坡的渗流影响较小．

4 结 论

1)不同裂隙深度土体内部含水量与孔压均存在一个最大影响深度，裂隙深度越大，影响深度越大．无裂隙土体体积含水量与孔压在降雨条件下随深度呈现先减小后不变的规律，而含裂隙土体体积含水量与孔压在降雨条件下随深度呈现先增大后减小最后保持不变．

2)土体渗透比大于10时体积含水量与孔压差异较小，而渗透比小于10的情况与大于10的情况差异较大，同时渗透比越大，土体表层含水量消散速度越快．

3)裂隙角度越小，土体内部含水量与孔压上升越快，同时，裂隙角度为0°与30°情况体积含水量与孔压变化规律较为接近，而裂隙角度为60°时体积含水量与孔压变化与前者差异较大．

4)不同类型降雨影响了含裂隙土体内部孔压与体积含水量的瞬时数值变化大小，对于孔压以及体积含水量的变化规律影响较小．