多馈入直流输电系统短路比评估方法综述

李 勇，倪晓军

（1.国网浙江综合能源服务有限公司，杭州 310014；

2.国网浙江省电力有限公司电力科学研究院，杭州 310014）

0 引言

交流系统和直流系统的相互作用很大程度上取决于交流系统和直流系统容量的相对大小，即短路比指标。CIGRE（国际大电网会议）工作组将交流系统的短路容量和直流额定功率的比值作为短路比，该指标被广泛应用于交直流系统强度的评估，被全世界范围内学者所认可[1]。

对于LCC-HVDC（基于相控换流器的高压直流输电）而言，短路比的大小决定了系统的强弱，也很大程度上影响了直流系统的运行性能[2]。SCR（短路比）越大，则直流系统的换相失败抵御能力越强、甩负荷后过电压水平越低且故障后系统恢复越快[3-4]。

随着德国慕尼黑联邦国防科技大学的学者Rainer Marquardt教授在2001年提出了模块化多电平换流器的概念，VSC-HVDC（基于电压源换流器的高压直流输电）技术得到迅速发展和应用。广大学者进而将短路比的指标扩展到了VSC-HVDC领域。VSC-HVDC短路比的定义沿用了GIGRE工作组提出的计算方法，只是短路比的大小对VSC-HVDC与LCC-HVDC特性的影响有所不同。理论上来说，只要系统的短路比大于1，VSC-HVDC理论上就有运行的可能性[5]。然而，当VSC-HVDC的短路比接近于1时，VSC-HVDC的稳定运行受到多方面的限制[6]。因而如何在弱系统条件下对VSC-HVDC的控制方式进行改进，使得VSC-HVDC在弱系统中也具备稳定运行的能力成为过去几年的研究热点[7-9]。

随着直流输电线路的增多，多条直流馈入同一个交流系统的情况越来越多，我国华东电网和南方电网的直流落点就十分密集。因此，将短路比指标从单条直流输电线路扩展到多馈入直流输电系统，用以衡量交直流系统间及直流系统与直流系统之间的相互影响程度，显得十分必要。其中CIGRE工作组提出的MISCR（多馈入直流短路比）应用最为广泛[10]。随后，广大学者对MISCR指标进行了改进，并提出了精确度更高的其他指标[11-14]。

同时，随着VSC-HVDC和LCC-HVD直流输电的发展，2种不同类型直流输电馈入同一交流系统的场景日益增多，研究2种直流输电技术的相互影响需要解决的重要问题之一是如何评判混合多馈入直流输电系统的短路比。对此，部分学者也提出了IESCR（基于运行阻抗的有效短路比）、AISCR（视在短路比增加量）等指标[15-16]。

本文主要针对多馈入直流输电系统的短路比评估方法进行研究，分析单馈入直流输电系统中短路比指标对直流输电系统的指导意义及其影响因素，针对多馈入高压直流输电、多馈入柔性直流输电和混合多馈入直流输电3种电网结构，对提出的短路比指标进行了分析。最后，对多馈入直流输电系统的短路比评估方法进行总结和对比，并得出结论。

1 短路比指标定义

1.1 LCC-HVDC的短路比指标

单馈入LCC-HVDC的系统结构示意如图1所示。

图1 LCC-HVDC的系统示意

图1中，Pd为直流额定功率，QF为无功补偿容量，Vt为母线电压，Zt和θ为系统等值阻抗幅值和相角，Es和δ为等值电动势幅值和相角。当考虑无功补偿装置时，通常用ESCR（有效短路比）来描述系统强度。根据CIGRE工作组的定义，SCR和ESCR的计算方法为：

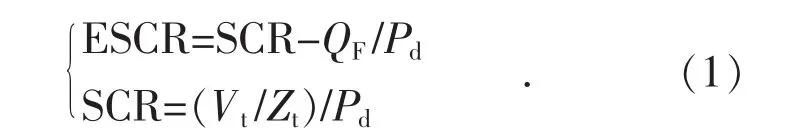
SCR的大小决定了交直流系统的强度，在文献[17]中，将SCR大于3的系统称为强交流系统，SCR界于2和3之间的系统称为弱交流系统，SCR小于2的系统称为极弱交流系统。LCC-HVDC能够正常运行存在一个最小的有效短路比，在更低短路比条件下，LCC-HVDC在理论上不具备运行的可能性。该短路比称为LCC-HDVC的CESCR（临界有效短路比），通常为1.5[17]。当然，文献[18]指出，LCC-HVD的CESCR数值大小还受到交流系统等效电动势、交流系统阻抗角、LCC运行方式等方面因素的影响。

SCR的大小对直流系统的运行稳定性有重要影响，主要体现在LCC-HVDC的换相失败抵御能力、过电压水平和故障后恢复速度等方面。

1.2VSC-HVDC的短路比指标

对于VSC-HVDC，其短路比计算一般也采用式（1）的方法，但如何利用短路比对VSC-HVDC系统的强弱进行划分还没有达成广泛共识。

由于VSC-HVDC可四象限运行，同时没有类似LCC-HVDC的换相失败问题，在传统的认识中，VSC-HVDC可运行在短路比接近1的条件下，即VSC-HVDC的临界短路比为1。但是该结论的正确性主要受到两个方面的影响：第一，与LCC-HVDC的短路比类似，采用式（1）计算VSC-HVDC的短路比，没有考虑交流系统等效电动势大小和交流系统阻抗角对CESCR的影响；第二，VSC-HVDC在临界短路比下的稳定性问题，即实际系统中，VSC究竟能否运行在短路比为1的条件下需要考虑控制器和控制参数的影响。

为了解决第一个问题，文献[19]分析了VSC可传输的有功功率与有效短路比、交流电动势和交流阻抗角的关系，得到了式（2）：

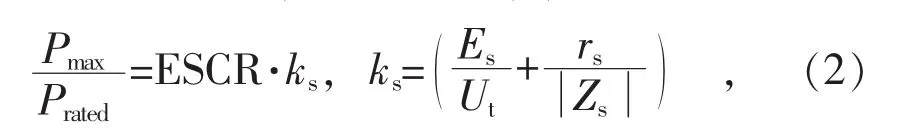
式中：Pmax为VSC-HVDC最大可传输功率；Prated为额定功率；Es为电源电动势；Zs和rs为电源等值阻抗和等值电阻。因此，当采用式（2）中的ks对VSC-HVDC的短路比指标进行修正时，即采用ESCR与ks的乘积来衡量VSC-HVDC的短路比指标时，可以得到当VSC-HVDC达到其有功功率极限时，其短路比确实为1.0。

针对VSC-HVDC在临界短路比条件下的稳定性问题，国内外学者开展了诸多研究。文献[20]建立了VSC-HVDC的小信号模型，通过根轨迹分析，指出锁相环的PI（比例积分）参数对系统能否运行在临界短路比十分重要。此后，诸多学者分析了VSC-HVDC控制器中锁相环参数、交流系统阻抗角、外环控制器参数对系统稳定性的影响[21-24]，并提出了功率同步控制、虚拟阻抗控制、改进型锁相环等控制器改进方式。上述研究的主要目的是使得VSC-HVDC能够运行在临界短路比条件下。

2 多馈入LCC-HVDC短路比评估

2.1 多馈入有效短路比

多馈入LCC-HVDC系统的示意如图2所示。图中 Zi（i=1，2，…，k）为各直流系统等值阻抗，Esi和 δi为各直流系统（i=1， 2， …， k）等值电动势幅值和相角。

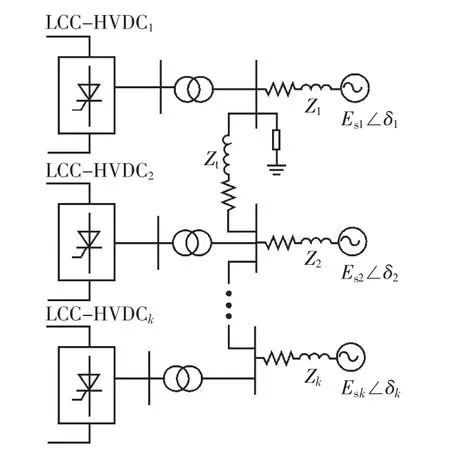
图2 多馈入LCC-HVDC直流输电系统示意

CIGRE工作组提出了MIESCR（多馈入有效短路比）来评估多馈入LCC-HVDC的有效短路比[25]。假设多馈入直流系统中有多个LCC-HVDC换流器，对于LCC-HVDC换流器Ci，其多馈入有效短路比MIESCR为：

式中：SCMVAi为换流器Ci所连接母线的短路容量；QFi为无功补偿容量；Pdci为Ci的额定功率；MIIFji为多馈入相互作用因子，为系统发生扰动时换流器Cj所在母线电压变化量与换流器Ci所在母线电压变化量的比值；Pdcj为多馈入系统中其他换流器的额定功率。

MIESCR的提出为多馈入直流输电系统的有效短路比评估方法提供了理论指导，但是该指标在衡量准确性上存在一些缺陷：第一，MIIF指标通过电磁暂态仿真得到，对于复杂多馈入系统计算较为困难；第二，该短路比为单馈入短路比的一种扩展，但是采用MIIF来描述其他换流站的影响是一种经验公式，缺乏理论依据。

2.2 多馈入有效短路比的改进

为了解决第一个问题，文献[11]提出了如式（4）所示的有效短路比计算方法：

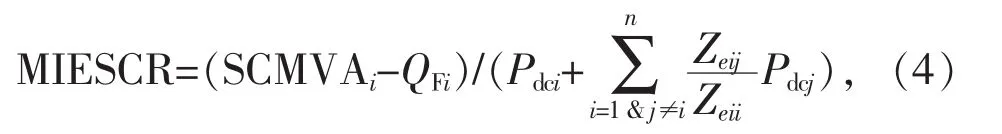
式中：Zeqij为从各直流母线看进去的等值节点阻抗矩阵Zeq的第i行j列元素。文献同时证明了公式（4）与公式（3）的等效性，为 MIESCR中 MIIF的计算提供了理论方法。

文献[26]指出，文献[11]中指出的方法虽然给出了MIIF的理论计算方法，但是当电力系统中存在较多动态元件时，如直流系统、FACTS（柔性交流输电系统）等，计算结果会产生较大误差。为此，文献[26]结合直流系统外特性方程，通过求解系统潮流雅各比矩阵，从理论上推导出多馈入直流系统MIIF求解过程，改进了MISCR的实用计算方法。

文献[13]对公式（3）进行了改进，提出了如式（5）所示的短路比评估方法：

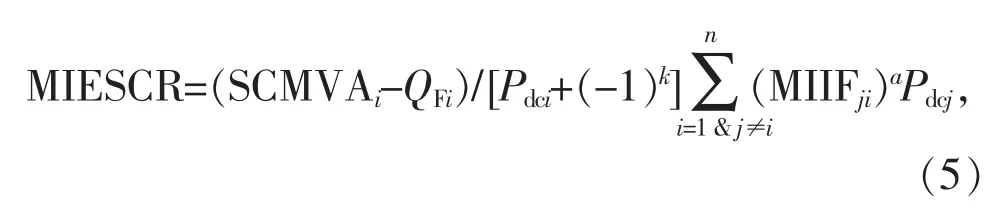
式中：当LCC为逆变站时，a=1，k=0；当LCC为整流站时，a=2.2，k=1。

该方法拓展了MIESCR的应用场景，可以用来评估含有整流站接入的多馈入直流系统强度。但是文章中a值通过仿真和线性拟合确定，系统配置变化时公式的有效性有待进一步验证。文献[14]利用等值阻抗的方法对文献[13]中a值的计算方法进行了改进。

上述文献针对公式（3）中MIIF的取值进行了优化和改进，为了进一步提高MIESCR的精确性，文献[14]和文献[27]提出了异于公式（3）形式的短路比评估方法。

文献[14]利用直流系统的潮流关系和系统特征方程，提出了基于多馈入系统等值直流视在功率的EESCR（等值有效短路比）指标，该指标提高了多馈入有效短路比评估的准确性。

文献[27]提出了一种计及LCC-HVDC交直流系统电压稳定的综合短路比强度指标。该文章通过对VSF（电压稳定因子）的分析来提出新的有效短路比指标。当多馈入直流系统处于静态电压稳定极限时，有VSFi=0。进而得出：

式中：Pd和Qd为直流有功无功功率；Sd为视在功率；U为母线电压；Yeq为系统等值导纳。

文献[27]进一步将公式（7）的左半部分定义为多馈入系统的综合短路比指标。同时，通过利用系统达到电压稳定极限时的临界短路比与1之间的偏差来验证了所提出指标的有效性。该指标更多地是从数学角度将电压稳定极限和临界短路比为1等值起来，该指标与传统ESCR等效性，是一个值得研究的问题。

显然，由于与理论推导相结合，相较于之前的基于经验的MIESCR及其改进的指标，文献[14]和文献[27]提出的指标精确性更高。

3 多馈入VSC-HVDC短路比评估

关于多馈入VSC-HVDC系统的短路比评估方法，目前未见有文献进行研究。主要原因如下：

（1）如何通过短路比大小对VSC-HVDC进行强弱系统划分，还没有一个普遍认可的结论。这点削弱了精确计算多馈入VSC-HVDC有效短路比的必要性和迫切性。

（2）在VSC-HVDC中，除了最基本的功率-相角（P-δ）曲线外，缺少其他的系统典型特性来验证所提出短路比指标的有效性。

（3）在多馈入VSC-HVDC系统中，MIESCR指标无法沿袭。当VSC-HVDC采用定交流电压控制时，母线电压变化量为0，MIIF为0或者无穷大，因此基于MIFF的MISCR概念无法在多馈入VSC-HVDC系统中得以拓展。

然而，当VSC-HVDC运行在接近其临界短路比，也就是诸多学者所述的VSC-HVDC连接弱交流系统时，VSC-HVDC在运行稳定性方面表现出了诸多限制因素，在该条件下对VSC-HVDC进行稳定性研究具有必要性和迫切性。同时，弱系统条件下VSC-HVDC的阻尼、惯量等特性可以有效评判系统稳定性的强弱。因此，在有效短路比接近1条件下VSC-HVDC的稳定性问题吸引了诸多学者的研究。这方面的研究在第1部分中已经有所阐述，也不是本文的研究重点，因此不再展开赘述。

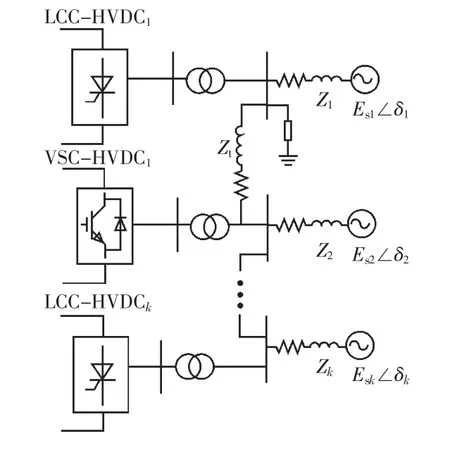
图3 混合多馈入直流输电系统示意

4 混合多馈入直流输电系统短路比评估

混合多馈入直流输电系统的示意见图3。

在包含VSC和LCC 2种类型换流器的多馈入直流有效短路比方面，也有学者开展了研究。

文献[28]提出了混合多馈入系统中LCC-HVDC有效短路比的评估方法，该文献沿用了SCR中短路容量的概念，将混合多馈入系统中的VSCHVDC换流器等效为电流源。但该电流源的数值是在假设VSC-HVDC的电流dq分量因为交流故障而保持在限值的条件下得到的，该指标的意义更多地在于为直流系统的故障恢复提供指导，与传统有效短路比的等效性方面有待进一步验证。

文献[29]提出了AISCR的概念，该短路比指标通过MAP（最大传输有功功率）曲线的插值算法获得。具体来说，首先计算得到在SCR0条件下单馈入LCC-HVDC的MPC（最大有功功率曲线），此时LCC-HVDC能达到的最大功率为MAPA，然后通过理论计算得到混合多馈入直流输电系统中所研究LCC-HVDC的MPC，假设在SCR1条件下LCC-HVDC也能达到最大功率MAPA，则认为混合多馈入系统的视在短路比增加量AISCR为（SCR1-SCR0）。图 4所示为混合双馈入系统中VSC-HVDC采用定交流电压控制时LCC-HVDC的AISCR值，由图可知，VSC-HVDC可以增强LCC-HVDC的短路比，并且当VSC-HVDC作整流器时效果更加明显。

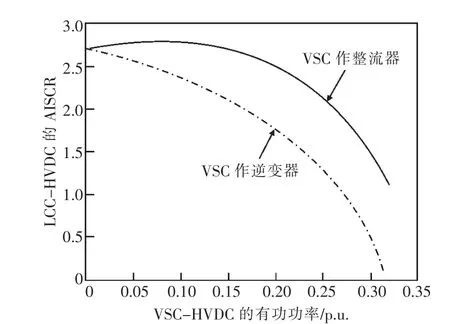
图4 双馈入直流系统中LCC-HVDC的AISCR值

该文献不仅提出了AISCR的概念，也研究了AISCR对LCC-HVDC的换相失败、暂态过电压、故障恢复特性的影响，研究发现AISCR对LCCHVDC的上述特性也具有指导作用。

文献[30]在文献[29]的基础上进行了扩展，研究了VSC-HVDC和LCC-HVDC两者之间存在联络线情况下混合双馈入系统的短路比，研究表明LCC-HVDC和VSC-HVDC两者间的电气距离越小，VSC-HVDC对LCC-HVDC短路比的改善程度越大。

文献[31]提出了IESCR指标。该指标的提出源于短路比的基本计算方法，其将所研究直流系统以外的换流器全部等效为运行阻抗，然后通过电路运算的方式来确定所研究线路的有效短路比，其关键点在于计算换流器的运行阻抗。在解决这个问题时，该文献提出首先需要得到换流器的小信号模型，利用该模型得到换流器交流侧电压和电流的关系，同时结合系统的阻抗矩阵，得到换流器的等效阻抗，其计算思路如图5所示。图5中idq为换流器交流侧电流dq分量，vdq为母线电压dq分量，A，B，C，D为由系统运行状态决定的系数矩阵，Ziequal为换流器运行阻抗。

图5 IESCR的计算方法

文献[34-35]利用系统雅各比矩阵和小信号模型，从特征根角度提出了直流多馈入系统的广义短路比和电力电子多馈入电力系统的广义短路比。使得短路比概念从单馈入扩展到多馈入、从直流设备扩展到电力电子设备，对短路比评估方法的进步具有重要意义。

5 结论

本文介绍了单馈入直流输电系统短路比概念，重点针对多馈入直流输电系统梳理和对比了主要的短路比评估方法，可为工程规划和系统分析提供参考，主要结论如下:

（1）多馈入LCC-HVDC的有效短路比研究相对成熟，以MIESCR的概念为基础，通过利用系统静态阻抗、动态阻抗、潮流、电压稳定性等特性，使得MIESCR的衡量准确性不断提高。

（2）开展多馈入VSC-HVDC的短路比研究具有重要意义，但目前研究VSC-HVDC的短路比指标及强弱系统划分的文献较少，现有研究主要针对VSC-HVDC接近临界短路比的工况进行稳定性分析。

（3）混合多馈入直流系统的短路比研究取得一定的成果，主要的衡量指标有AISCR和IESCR 2种，短路比评估方面还处于在不断发展的过程中。

（4）在短路比评估方法的改进方面，提出一种通用有效短路比评估方法，对于研究交直流系统及直流与直流间的交互影响具有重要作用，且短路比指标的准确性和易操作性等方面需要不断发展改进。

（5）目前短路比指标一般都是用MPC或者P-δ的静态指标来定义和验证，短路比指标对于系统的动态特性，如LCC-HVDC的换相失败特性或者VSC-HDVC系统响应速度等的定量描述还有待研究。