基于独立分量技术的类GIFT算法S盒逆向分析
马向亮 李 冰 习 伟 陈 华 陈财森
1(中国科学院软件研究所可信计算与信息保障实验室 北京 100190)2(中国科学院大学 北京 100049)3(国家信息技术安全研究中心 北京 100084)4(南方电网科学研究院 广州 510663)5(陆军装甲兵学院演训中心 北京 100072)
尽管目前密码学的一个基本安全假设为,密码算法的安全性依赖于密钥及密钥的长度,而不是算法本身的保密性.然而在很多时候,政府或国防军队为了加强安全级别,或企业为了商业应用,对一些密码算法、部件进行保密或修改.在此情况下,对带有未知算法实现的密码系统或模块进行安全性评估至关重要,其中逆向分析是进行安全性评估的前提.逆向分析将直接影响到密码算法实现测评的力度.
目前,已存在的逆向分析方法主要有数学逆向分析[1]、基于故障注入技术的逆向分析[2]和基于侧信道技术的逆向分析[3]等.和数学分析方法相比,基于侧信道和故障注入等旁路技术的逆向分析具有代价低、通用性强等优势.另外,芯片解剖逆向[4]也是一种逆向分析方式,通过还原电路进行逻辑判断、分析,然而由于周期长、代价高、可行性低等原因,该方法不适宜现在工艺发达、高度集成的加密电路芯片.
1) 数学逆向分析
在欧洲密码年会(EUROCRYPT2001)上,文献[1]提出了一种结构分析方法,目的是在减少轮上进行SPN机构的逆向分析.考虑到分析的高复杂度,为了建立未知操作输入和输出之间的关系,利用该方法通过线性和非线性操作发现多重集的特征.在2011年文献[5]使用这种方法实现了类PRESENT算法的逆向S盒分析.
2) 基于故障注入技术的逆向分析
基于差分故障技术的逆向分析模型[6]是1997年由Biham等人最初提出的,即错误发生位置可以控制,但错误的结果未知.他们提出在一个封闭的防篡改设备(如智能卡)中可以逆向恢复未知S盒结构.2014年Clavier等人基于无效故障模型对类AES算法进行了逆向分析[7].在该模型下,即使敌手在不知道密钥,对未保护的或带有常用布尔掩码和乱序防护措施的算法软实现,依然能够完全逆向恢复所有未知参数.
3) 基于侧信道逆向分析
① 传统侧信道逆向分析
2008年文献[8]提出基于硬件设计的未知Feistel结构的逆向分析方案,使用选择明文攻击的侧信道攻击可以逆向分析恢复.2010年文献[9] 提出2种攻击方法,一种是攻击线性反馈寄存器结构算法的未知线性部件;另一种是恢复未知的非线性函数如S盒.2011年文献[10]使用故障注入同时对2个常用的DES和AES算法逆向恢复未知S盒.2016年文献[11]提出了基于线性回归攻击的新型侧信道逆向分析方法,与之前的侧信道逆向分析相比,该方法使用更少的先验知识,并能给出更多的密码实例.
② 基于独立分量攻击(ICA)的逆向分析
2017年文献[12]提出了一种新型的侧信道分析技术,即基于独立分量技术[13](independent com-ponent analysis, ICA)的侧信道分析方法.盲源分离问题是指在原始信号被混合输出后,如何从一组被观测的混合信号中分离出没有被观测到的原始信号.独立分量技术可将侧信道泄露转化为有效的独立分量观测,并直接从泄露的曲线中恢复出中间轮的某个中间状态.与传统的侧信道分析策略不同,该方法没有采取“先猜测后确定”,而是采用了直接恢复的分析策略.该方法可用于未知密码算法的逆向分析中.相比于已有方法,该方法对算法类型和实现条件的限制较少,攻击复杂度较低,适用性好.文献[12]同时给出了一个针对DES实现的攻击实例,结果显示该方法恢复出S盒的等价形式仅需几百条能量迹.
综合以上相关工作,侧信道在逆向分析中具有很大的优势,在一定程度上降低了逆向分析的复杂度,可行性较强.进一步,独立分量技术在侧信道逆向分析中的应用使得侧信道逆向分析攻击的适用性更强、复杂度更低.鉴于独立分量技术的特点,在侧信道逆向分析中,特别适用于密码算法具有比特打乱或比特置换部件.
GIFT算法[14]是在密码硬件与嵌入式系统会议(CHES 2017)上提出的一种轻量级分组密码算法.自该算法提出后,已出现一些针对它的分析结果,但尚没有针对它抵抗逆向分析的安全性评估.
本文提出了一种基于独立分量攻击技术的类GIFT算法S盒逆向分析方法.我们针对GIFT算法中P置换的比特置换特点,构造了有效的独立分量观测值,并从得到的功耗曲线中直接恢复出了第一轮P置换输出值.因此在明文已知的情况下,S盒的内容可以恢复出来.另外我们也进行了GIFT算法的逆向分析实验,实验结果验证了本方法是可行的.最后,我们针对独立分量技术的攻击特点给出了相关防御建议.
1 预备知识
1.1 ICA介绍
1.1.1 ICA定义
ICA是信号处理中解决盲源分离[12](blind source separation, BSS)问题的一种常用技术.利用该技术实现了鸡尾酒会假设的问题,即在酒会上多人在一起讲话,房间的多个麦克风将大家的声音混合在一起经信号转换后进行记录,如何由记录的混合信号还原回原始的各个独立的信号.
ICA模型假设观察到的混合信号变量Y=(y1,y2,…,ym)T,这些变量是由n个独立未知源信号S=(s1,s2,…,sn)线性混合而成.因此混合信号yj和源信号S之间存在关系yj=aj,1s1+aj,2s2+…+aj,nsn,其中ai,j是未知的混合系数.混合信号也可以使用向量表示为Y=AS,A为未知混合系数矩阵.在实际信号处理过程中,通常会考虑噪声的干扰,ICA模型修正为Y=AS+N,N为未知的不可预测噪声,符合正态高斯分布.ICA的作用是仅仅通过观察Y来恢复源信号S和混合系数矩阵A.
1.1.2 ICA约束与不确定性
由ICA定义可知,在混合系数矩阵A未知情况下,由Y直接恢复S是非常有挑战性的.使用ICA方法解决这个难题,需要满足以下3个条件:
1) 观测信号相互独立;
2) 观测信号必须非高斯分布;
3) 观察个数大于等于源信号个数 (m≥n).
由于源信号S和混合系数矩阵A未知,基于ICA模型恢复必然带来了一些不确定结果,不确定性主要有以下2个方面:
1) 无法确定源信号的次序.这个是显而易见的,选择一个可逆矩阵P,由Y=AS,则Y=AP-1PS,若A和S是解,则AP-1和PS也是解.
2) 无法确定源信号的维度.任何一个源信号都可以通过乘一个标量然后在矩阵A中对应的列中除以该标量抵消掉.
1.1.3 ICA算法
ICA自从提出开始已有大量的研究成果,不同的处理算法相继提出.按步骤分类为以下3种:
1) 批处理算法.成对数据旋转法(Jacobi)、特征矩阵的联合近似对角法(JADE)等;
2) 自适应算法.串行矩阵更新及其自适应算法、扩展的Infomax法等;
3) 探查性投影追踪法.梯度算法、固定点算法(Fast ICA)等.
以上算法中Fast ICA类最常用,本文使用该算法进行实验.
1.2 GIFT算法介绍
GIFT算法是Banik等人在CHES2017年会议上提出的SPN结构轻量级算法,是PRESENT算法的升级版,修正了PRESENT算法已知的缺点.该算法有2个版本,密钥都是128 b,明文分组有区别分别为64 b和128 b.本文实验使用的是64 b版本,以64 b为例介绍,但是64 b和128 b攻击效果是一样的.
GIFT算法一共28轮运算,每轮运算由3个步骤组成:S盒替换、比特P置换和与密钥异或运算.
1.2.1 初始化
将加密的64位明文bn-1bn-2…b0作为一个密码状态S,其中b0是最低有效位.也可以将S表示为4位半字节排列,即S=ws-1‖ws-2‖…‖w0,其中s=16.密钥128位可以表示为16位的字排列,即K=k7‖k6‖…‖k0.
1.2.2 S盒替换
S盒是GIFT算法中唯一的非线性部件,将状态S中的每半个字节经查表替换为相应的值.wi←GS(wi),∀i∈{0,…,s-1}.S盒GS如表1所示,表1中的数据使用十六进制.
1.2.3 比特置换
比特置换用来打乱原来的位顺序,将第i位的状态置换为第P(i)位,即bP(i)←bi,∀i∈{0,…,n-1}.P置换表如表2所示.
1.2.4 密钥异或
32位的轮密钥被分为2个16位字排列,即RK=U‖V=us-1…u0‖vs-1…v0.U和V分别和密码状态b4i+1和b4i进行异或运算.即b4i+1←b4i+1⊕ui,b4i←b4i⊕vi,∀i∈{0,…,15}.

Table 1 GIFT S Box GS表1 GIFT算法的S盒GS

Table 2 GIFT Bit Permutation表2 GIFT算法P置换表
与轮密钥异或运算完的密码状态的第63,23,19,15,11,7和3位分别与1和6位轮常数进行异或运算.轮常数为C=c5c4c3c2c1c0,即
bn-1←bn-1⊕1,b23←b23⊕c5,
b19←b19⊕c4,b15←b15⊕c3,
b11←b11⊕c2,b7←b7⊕c1,b3←b3⊕c0.
1.2.5 密钥编排和轮常数
轮密钥RK32位由2个16位字排列组合而成,即RK=U‖V.U←k1,V←k0.密钥每轮更新一次,k7‖k6‖…‖k0←k1>>>2‖k0>>>12‖…‖k3‖k2.其中,>>>i指的是16位字循环右移i位.轮常数使用6位线性反馈寄存器进行更新,6位初始值为0,需要先更新才能使用,更新函数为(c5,c4,c3,c2,c1,c0)←(c4,c3,c2,c1,c0,c5⊕c4⊕1).每轮常数如表3所示:

Table 3 Rounds constants表3 轮常数
2 ICA逆向分析
2.1 ICA逆向分析模型及算法
在本节中,我们详细介绍如何将ICA用于侧信道逆向恢复.依赖数据侧信道泄露模型以及数据之间的独立与非高斯性,通过深入研究算法的特定结构,构造符合ICA攻击条件,将侧信道中需要恢复的中间值数据问题转换为ICA问题.
侧信道常用的数据依赖映射模型为汉明重量模型.对于中间值数据n位的能量泄露值可以表示为
L(x)=a1x1+a2x2+…+anxn,αi∈{0,1},
其中,xi表示中间值x的二进制表示.能量泄露值的汉明重量模型满足ICA线性混合条件.在侧信道环境中,xi是比特信号,取值0或者1,服从伯努利分布,天然满足非高斯和独立性.在此基础上,构造符合ICA观测成为ICA在侧信道逆向分析的关键,由于该问题需要结合特定算法结构进行分析解决,针对本文的GIFT算法观测将在3节介绍.
通过结合算法结构和侧信道相关理论,使得ICA算法在侧信道环境中适用于逆向分析,通过观察T个中间状态x=(x(1),x(2),…,x(T)).由比特置换可知,每个比特之间互相独立,可表示为xi=(xi(1),xi(2),…,xi(T)).相对应的观测为Y=(y1,y2,…,ym)T,而每比特观测为yi=(yi(1),yi(2),…,yi(T)).如算法1所示.
算法1. 用于侧信道逆向的ICA算法[15].
输入:T条能量迹;
① 收集m个观测Y=(y1,y2,…,ym)T.
② 利用Fast ICA算法,得到原观测的n个实值独立分量(IC1,IC2,…,ICn).

while ΔL>thresholddo
E-Step:用当前的参数θ(j),计算对数似然期 望函数L(θ(j));
M-Step:计算最大化对数似然期望函数L的 参数(θ(j+1));
end while

电子噪声在能量曲线采集中不可避免,噪声会改变能量迹中的能量值,从而对逆向分析带来了难度.一个简单直接的办法就是改善采集硬件条件尽可能降低电子噪声和转换噪声,另外就是通过多次采集求均值、滤波技术、奇异谱分析技术等预处理技术,减少噪声的干扰.S盒是分组密码算法的关键非线性部件,它是逆向分析研究的主要分析对象.在针对S盒的逆向分析中,利用算法的特殊结构,ICA可以从能量迹上的能量值直接恢复S盒的输出,本文提出基于ICA的逆向分析模型如图1所示:

Fig. 1 ICA model for SCARE图1 ICA侧信道逆向分析模型
由图1该模型下逆向分析S盒的步骤如下:
1) 选择随机明文,经加密算法M次加密运算,得到M条能量迹,也就得到一组M长的源信号观测,而且相互之间是独立的;
2) 选取S盒输出的能量迹上的相应值观测作为能量值.能量值依据示波器的采用率和分辨率,而且和采样时间长短有关.需要从能量迹上识别出所需的点;
3) 使用Fast ICA算法对能量值进行攻击,恢复出S盒输出二进制序列;
4) 将二进制转化为16进制数据,作为算法S盒输出;
5) 由于S盒输入已知,由输入和输出逆向分析出S盒结果.
2.2 ICA逆向分析成功率

其中,
由于ICA方法直接恢复密码算法的某个中间值,可以使用正确信号(Xc)与ICA计算恢复信号(Xr)之间的最小距离来判断恢复结果的有效性.随着能量迹的增多,D(Xr,Xc)将变大,因此ICA逆向分析成功率可定义为
由D(Xr,Xc)定义可知,ICA逆向恢复成功率最小为0.5;若成功率比较大,远远大于0.5,则说明ICA成功恢复出S盒中间值;若成功率和0.5差不多,则说明ICA计算返回的中间值不可信.
3 GIFT算法逆向分析
本节将详细介绍GIFT算法利用ICA技术进行逆向分析.GIFT算法主要由3部分组成,S盒置换、P置换和与轮密钥、常数异或.因此在GIFT算法ICA观测中,选择比特置换作为观测源,满足ICA观测需求,如图2所示.

Fig. 2 Observations GIFT图2 GIFT算法观测图
在这里我们将分析第1轮S盒输出(它同时也是第1轮P置换的输入)的能量泄露,由于P置换是逐比特进行的,比特之间相互独立,这种方法特别适用于构造ICA观测.xi=(xi(1),xi(2),…,xi(T)).相对应的观测为Y=(y1,y2,…,ym)T,而每比特观测为yi=(yi(1),yi(2),…,yi(T)).通过调用ICA算法,可以直接恢复出S盒的输出值.
随机选择2 000组明文数据,使用GIFT算法对该数据进行加密,得到2 000条能量迹.由上面观测图2和先验知识可知,第1个S 盒输出比特置换位分别为0,17,34和51,这4个比特之间相互独立满足ICA观测要求,因此能量迹上存在4个点产生的能量值作为观测值.以这种观测方式,得到2 000组中间值观测,其他S盒执行类似观测.

Fig. 3 GIFT trace with SNR=0.01图3 信噪比为0.01的GIFT能量迹
将2 000组观测值作为ICA逆向分析算法输入数据进行计算.算法计算完成返回一个2 000行4列二进制数据0或1矩阵.将矩阵中每行4列二进制数据按照相应权重计算为一个16进制数据,由此得到一个2 000行向量,每个值对应为S盒输出数据.由于2 000个明文已知,对应的S盒输出数据已由ICA算法计算获得,从而完成GIFT算法S盒逆向恢复.
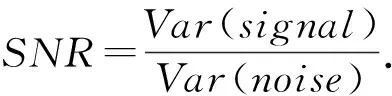

Fig. 4 GIFT trace with SNR=0.04图4 信噪比为0.04的GIFT能量迹

Fig. 5 GIFT trace with SNR=1图5 信噪比为1的GIFT能量迹
由图3和图5能量迹可以直观得出,噪声对侧信道分析的影响也可以从能量迹上直观的看到,信噪比小的能量迹波动很大.信噪比为1的能量迹波动明显小于信噪比为0.01的能量迹波动.利用比特置换P为观测源,通过选取能量迹上4个点能量值作为ICA观测值,通过ICA算法对上述仿真的7组不同信噪比能量迹进行逆向分析的成功率如表4所示.

Table 4 Success Rates Based on ICA for Recovering S Box with Different SNR

Fig. 6 Success rates based on ICA for recovering GIFT S box图6 ICA逆向分析GIFT算法S盒成功率
图6给出了GIFT算法首轮第一个S盒ICA逆向恢复结果.实验中,没有噪声的观测值恢复很快,无疑正确的恢复出了结果;信噪比在接近1以及大于1时的成功率都为1;可以看出信噪比为0.04的逆向成功率为0.757 5,效果也比较理想;但在信噪比为0.01时的成功率较低,仅有0.627 5.
实验中,统一使用的能量迹2 000条,成功率为1的逆向分析实际上用不了2 000条.成功率小于1的随着能量迹条数的增多,成功率会逐渐增大,但是信噪比较低的,成功率不会有大的改善.另外,本实验没有使用任何降噪技术,如果能量迹进行降噪预处理后再进行观测,那么效果会得到改善,可以预计的是攻击条数会有相应减少,信噪比太低的,成功率仍然不会有很大提高,这是由于有用信息已被噪声淹没掉.
4 结 论
对带有未知算法实现的密码系统或模块进行逆向分析具有重要意义,侧信道方法具有一定的优势,在一定程度上降低了逆向分析的复杂度,而且可行性强.与传统的侧信道逆向分析相比,本文提出的一种基于独立分量攻击技术的类GIFT算法S盒逆向分析方法,不需要进行猜测和确定.我们针对该算法中P置换的比特置换特点,构造了有效的独立分量观测值,并从仿真得到的能量迹中直接恢复出了第一轮P置换输出值,从而成功进行逆向分析.
本文提出的基于ICA的逆向分析方法和模型,基于P置换的比特置换特点.对于某些算法结构中,并不存在比特置换特点如国密SM4算法,相互之间不独立,因此无法进行有效观测.如何构建符合ICA攻击的独立观测是一个难点,可以尝试选择特定明文或使明文与一个常数异或,使得该算法在第二轮加密时达到某些观测值之间相互独立.
如果算法工程采用软实现方式,针对本文提出的基于独立分量技术的逆向分析,使用大噪声干扰是一种方案,该方法在一定程度上增加了该攻击难度,如果噪声足够大,则信号将淹没,信噪比很低,无法恢复出有用信号.对于硬实现,暂时没有找到合适的线性模型,观测值之间相互不独立,分离信号有一定的难度,是目前该方法的局限性,因此硬实现是一种比较理想的防护方案.最后统筹考虑安全因素和性能代价,选择没有比特置换特点的算法,使得攻击者无法构建符合ICA攻击的独立观测.尽管该方法不够完美,有一定的局限性,但本方法为密码分析者和测评机构提供了一种新的思路和评估手段,对于其他未知算法的逆向分析也具有参考意义.

