基于遗传算法的FSC赛车转向梯形设计及优化

章文忠，李健，徐生明，陈飚，张众华

(四川交通职业技术学院机电工程系，四川成都 611130)

0 引言

中国大学生方程式汽车大赛(简称“中国FSC，Formula Student China”)是一项由中国汽车工程学会组织国内汽车相关专业在校学生参加的汽车设计与制造竞赛，是培养中国汽车工程师的摇篮。经过八年的赛事积累，中国大学生方程式赛车的综合性能不断增强，提升赛车动态性能逐渐成为赛车底盘开发设计中的重点、难点。传统的阿克曼转向几何理想模型中假定轮胎为刚体，从运动学的角度近似地保证了车辆在曲线行驶过程中4个车轮围绕同一瞬心进行纯滚动，可有效减少轮胎磨损并保证轮胎磨损的一致性，提高车辆轮胎的使用寿命[1-2]。但方程式赛车为了提高轮胎和赛道之间的黏着系数，广泛使用较软的光头轮胎，其侧偏刚度小于传统车辆，因此在赛车阿克曼转向几何的设计中应当考虑轮胎侧偏角的影响，而各参赛车队在转向梯形的设计和优化中很少考虑轮胎侧偏角。本文作者立足于提升赛车动态性能和降低轮胎磨损，以赛车动力学理论为基础进行赛车转向运动学设计，分别推导了基于刚体轮胎和考虑轮胎侧偏角的阿克曼转向理想模型，并以此为目标函数，建立了基于遗传算法的转向梯形断开点优化模型，最后在ADAMS/Car中建立了赛车虚拟样机，并对两种优化后的转向梯形模型进行了仿真与分析。

1 阿克曼转向理想模型

1.1 基于刚体轮胎的阿克曼转向模型

传统的阿克曼转向模型假定赛车转向时速度很慢，一般在5 km/h以下，其侧向加速度很小，可忽略轮胎侧偏角，因此在阿克曼转向模型中将轮胎视为刚体。如图1所示，在赛车转向过程中，为了使各个车轮都处于纯滚动状态，则要求所有轮胎都绕同一个瞬时转向中心作圆周运动，在忽略轮胎侧偏角的情况下，轮胎的速度方向与轮胎平面平行，因此转向瞬心就是赛车后轴的延长线与前轴轮胎旋转中心线的延长线的交点O。结合赛车基本参数，可得赛车前轴内、外车轮转角与车辆轴距、轮距之间的理想关系，如式(1)所示。目前这种阿克曼转向理想模型被各参赛车队普遍采用， 并用于优化转向梯形的硬点位置参数。

(1)

式中：L为赛车轴距；A、B分别为主销中心线的延长线与地面的交点，K为A、B之间的距离。

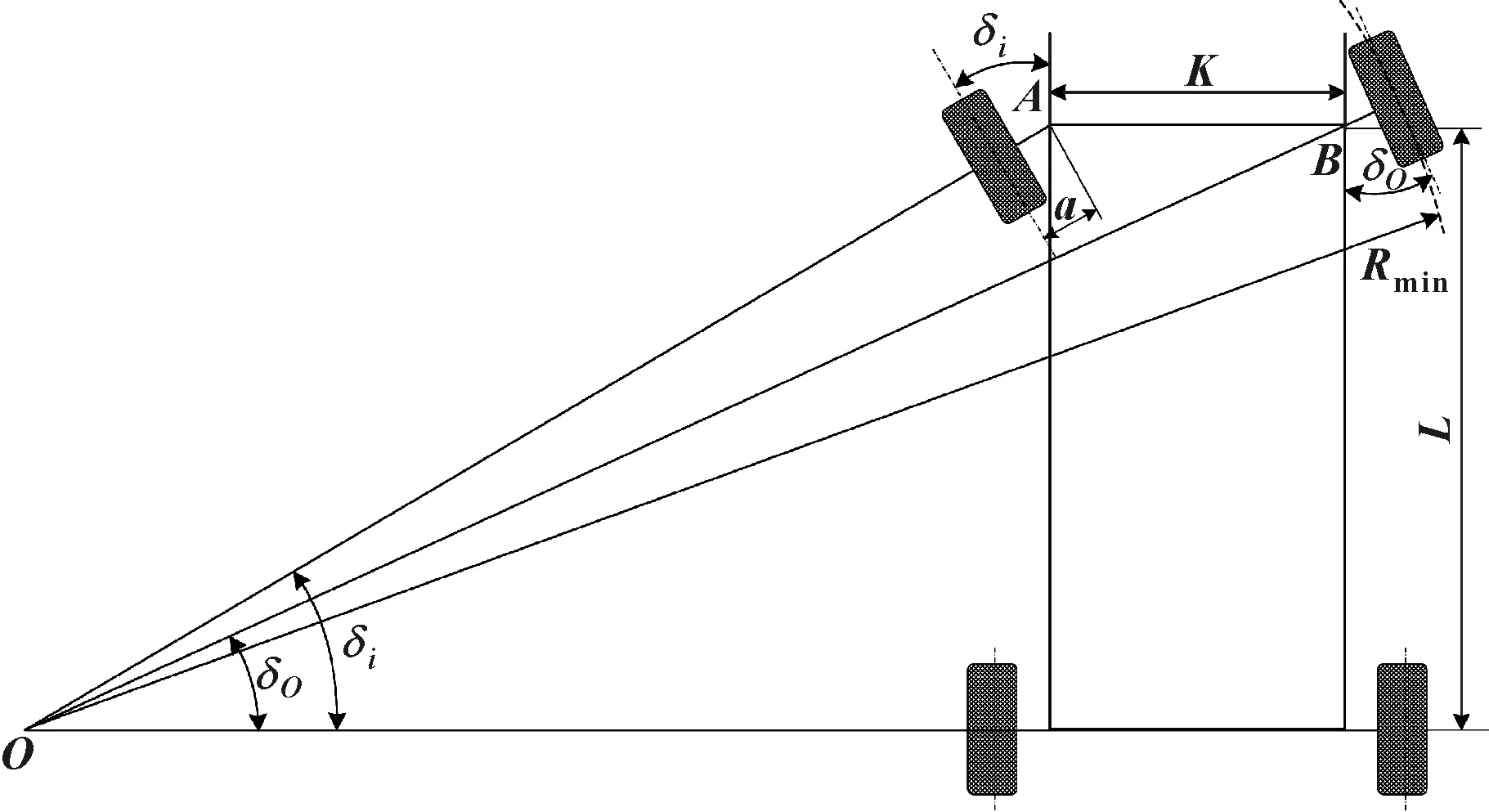
图1 基于刚体轮胎的阿克曼转向几何示意图

1.2 考虑轮胎侧偏角的阿克曼转向模型

赛车轮胎普遍采用半热熔的光头胎，胎地黏着性能好，附着系数高，在专用赛道上一般可达到2.0左右，轮胎的侧偏刚度比乘用车小，在相同侧向加速度条件下，轮胎侧偏角大于传统车辆。在比赛过程中，耐久赛、高速避障赛和燃油经济性赛的合计总分占据比赛总成绩的60%，是大学生方程式竞赛的关键赛项，同时赛道具有弯道段多、直道段少以及绕桩频繁等特点。为了获得最佳的动态成绩，缩短赛车过弯时间是赢得比赛的关键，因此赛车常行驶在较高侧向加速度下，轮胎的侧偏角不可忽略。

如图2所示，在赛车转向行驶时，各个轮胎都产生了侧偏角，使得各个轮胎中心的瞬时速度方向都偏离了轮胎的对称线，轮胎产生了速度偏角β，此时各个轮胎的瞬时转动中心仍然在与其速度矢量相垂直的直线上，相交于O′。可见，由于轮胎侧偏角的影响，赛车的瞬时转向中心相对后轴轴线向前偏移了一个距离ΔL。

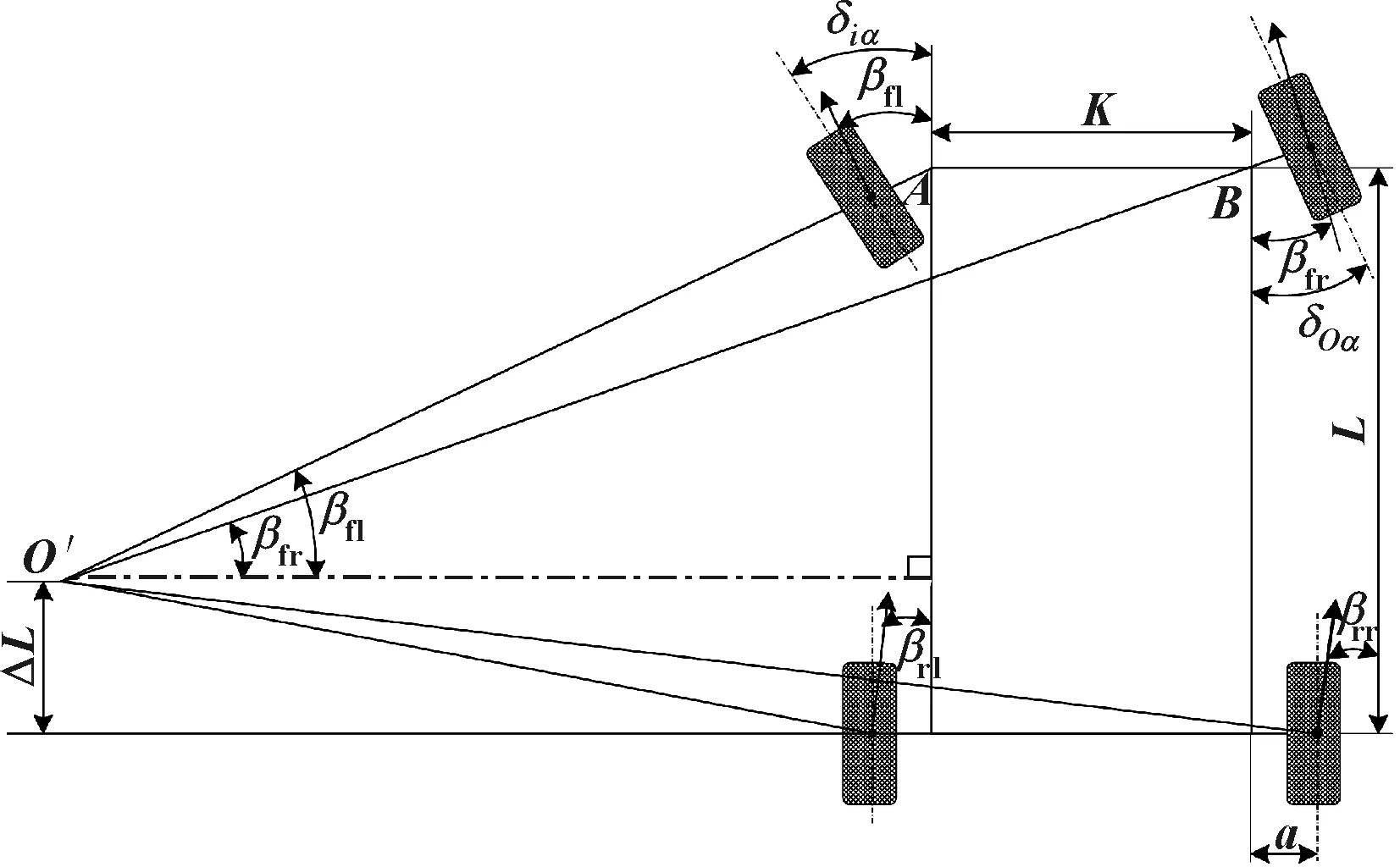
图2 考虑轮胎侧偏角的阿克曼转向几何示意图

根据车轮转向角与轮胎速度偏角和轮胎侧偏角之间的关系[3],可得式(2)。

αj=δj-βj

(2)

式中：αj(j=fl、fr、rl、rr)表示各个轮胎的侧偏角，此处不考虑轮胎侧偏角的正负符号。

由赛车结构参数和阿克曼转向几何关系可得式(3)、式(4)，即为考虑轮胎侧偏角条件下的阿克曼转向理想模型。

(3)

(4)

考虑到赛车在专用赛道中竞技行驶，且弯道多直道少，轮胎侧偏角在3°～6°范围内时侧向力达到极限状态，文中取αfl=αfr=αrl=αrr=3.5°。

1.3 前轴内外轮转角关系

为了使赛车获得良好的操控稳定性和空间布置，广泛采用双横臂独立悬架和断开式转向梯形设计[5]，前轴内、外轮转角关系如图3所示。

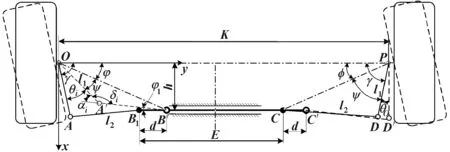
图3 内外侧车轮转角关系图

其中：l1、l2分别表示转向节臂和横拉杆的长度；γ为梯形底角；h为齿条中心至前轴距离；B、C为横拉杆断开点；E为断开点之间的距离。图3所示为赛车向左转弯行驶，齿条向右侧移动以推动左、右车轮偏转，转向梯形OABCDP即决定了左右车轮的转角关系。

当齿条向右移动距离为d时，通过转向横拉杆拉动左梯形臂，左侧车轮转角为θi，转向节臂和横拉杆由实线位置将运动至虚线位置，运用平面运动分析法可得转角θi与齿条位移d的关系如式(5)所示。

(5)

同理，右侧车轮偏转角度为θO，右侧转向节臂和横拉杆由实线位置移动至虚线位置[4]，通过平面几何关系可建立式(6)—(8)。

(6)

(7)

θO=ψ+φ-γ

(8)

因此结合式(5)—(8)，即可得到左、右车轮在齿条运动下的转角关系。

2 基于遗传算法的转向模型优化

遗传算法是一种模拟自然选择和群体遗传机制的优化方法，通过应用编码技术来模拟生物染色体结构。在转向梯形断开点优化中，将“优胜劣汰，适者生存”的生物进化原理引入待优化的编码群体，通过计算机的迭代计算，找到满足判定条件的目标参数。

(1)确定决策变量和约束条件

将梯形底角γ、转向节臂长度l1、齿条中心线至前轴距离h以及横拉杆长度l2作为优化转向梯形的决策变量，以同阿克曼转向理想模型确定的转角关系曲线的差值平方和最小为目标，即简化为求解多变量单目标的优化问题。

约束条件确定了优化过程中各决策变量的取值范围，只要能囊括决策变量的最优值即可，可通过赛车转向梯形的总体布置设计来进行估算。各决策变量的值域范围如表1所示。

表1 各决策变量的值域范围

(2)建立优化模型

由式(5)—(8)确定的左、右车轮在齿条运动下的转角关系为优化模型，其中包含了所有的决策变量。采用MATLAB编写优化程序，进行迭代计算，直到计算出最优的决策变量值。

(3)编码决策变量

选用长度为10位的二进制编码串分别表示4个决策变量γ、l1、h、l2，10位二进制编码串可以表示0～1 023之间的1 024个不同的数，即将γ、l1、h、l2分别离散成为1 024个不同的离散点。从取值范围的最小值到最大值，让它们依次对应0000000000(0)～1111111111(1 023)之间的二进制编码串。

(4)解码决策变量

解码是需要将长度为40位长的二进制编码串分成4个10位长的二进制编码串，然后分别将它们转换为对应的10进制整数数值，分别标记为γc、lc1、hc、lc2。根据个体编码方法和值域离散化方法，按照式(9)将代码变量转换为实数变量γ、l1、h、l2。

(9)

(5)个体适应度评价

在优化计算中，将左侧车轮的转角取值离散化，将右侧车轮转角与理想的阿克曼转向模型确定的右侧转角之间的误差平方和作为目标函数，即遗传算法中每个体的环境适应度值，其数值越小，决策变量越接近最优值，证明个体适应性越强，目标函数如式(10)所示。

(10)

(6)确定基本参数

基本参数如表2所示。

表2 基本参数

(7)优化结果

决定阿克曼转向几何的4个决策变量的优化结果如表3、表4所示。

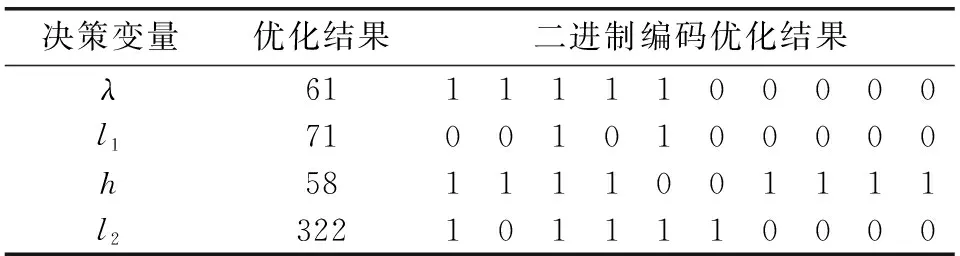
表3 基于刚体轮胎阿克曼转向理想模型优化结果

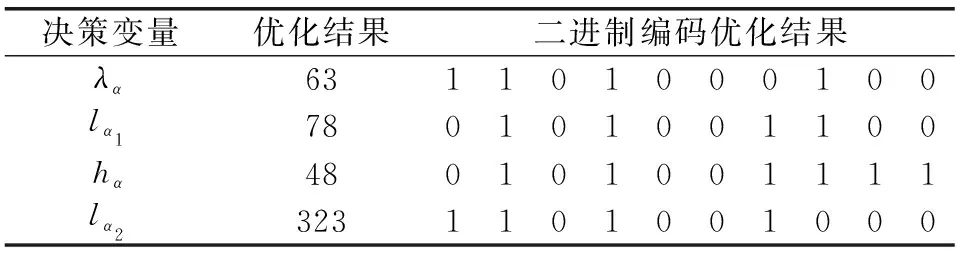
表4 考虑轮胎侧偏角的阿克曼转向理想模型优化结果

基于刚体轮胎假设和考虑轮胎侧偏角影响的阿克曼转向理想模型与优化后的转向梯形决定的内外轮转角关系的对比曲线如图4所示。

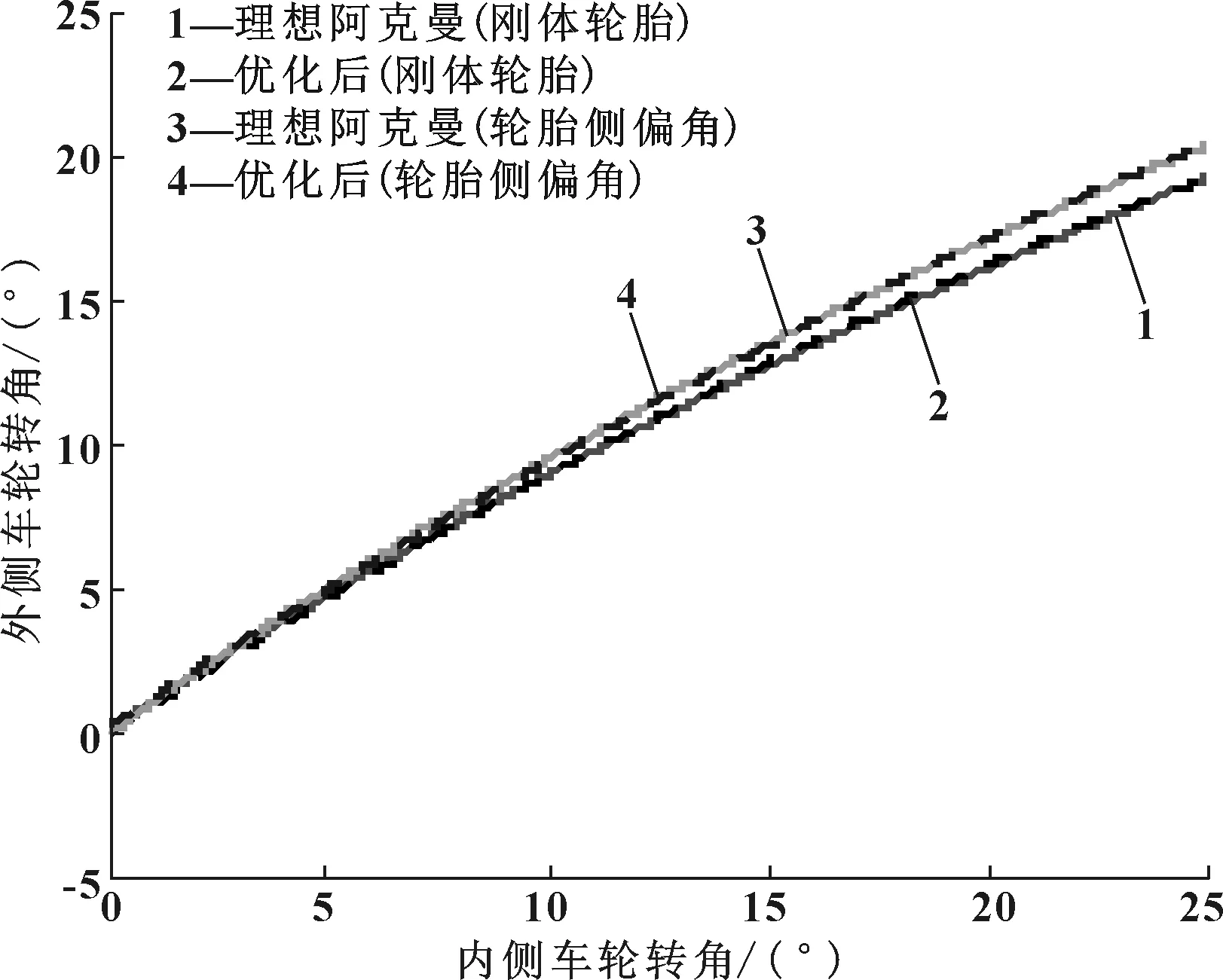
图4 两种理想模型优化前后对比图

优化后的内外轮转角关系曲线与理想模型符合度均较高，证明转向梯形的设计和基于遗传算法的优化模型是有效的；此外，可以看出：考虑侧偏角影响的转向梯形使外侧车轮获得更大的转角，在赛车方向盘大转角输入时尤为明显，使赛车具备更小转弯半径的行驶能力，可提高赛车转向灵活性，同时更好地减小了轮胎的磨损量。

图5所示为个体适应度值与进化代数之间变化曲线，适应度值越小，即证明转向梯形决定的内外轮转角关系与阿克曼转向理想模型之间的符合程度越高，可以看出在进化的初期，适应度值快速减小，逐渐放缓并收敛于某个适应度值，由此证明文中设计的基于遗传优化算法的优化模型具有较好的适应性和优化效果，并具有一定的应用价值和现实意义。

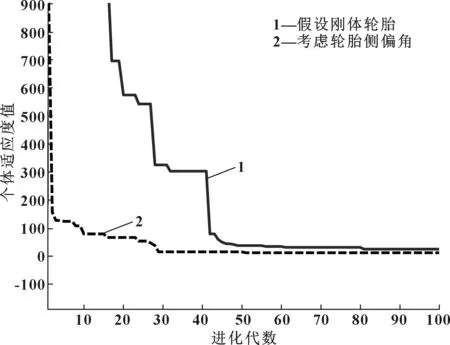
图5 个体适应度随进化代数的变化曲线

3 虚拟仿真试验

为了进一步验证考虑轮胎侧偏角对赛车转向梯形优化设计的影响，在ADAMS/Car中建立了赛车整车动力学模型，分别将两种优化后的赛车转向梯形模型应用于赛车虚拟样机中[6]，在方向盘角阶跃工况下进行仿真计算。如图6所示，在稳态转向行驶时，采用考虑轮胎侧偏角的转向梯形模型使赛车轨迹半径减小；赛车纵向速度曲线如图7所示；各个轮胎侧偏角变化曲线如图8所示，可以看出考虑轮胎侧偏角的转向梯形使赛车的外侧车轮的侧偏角在稳态转向行驶工况下更大，分析其原因是由更大的偏转角响应引起的。

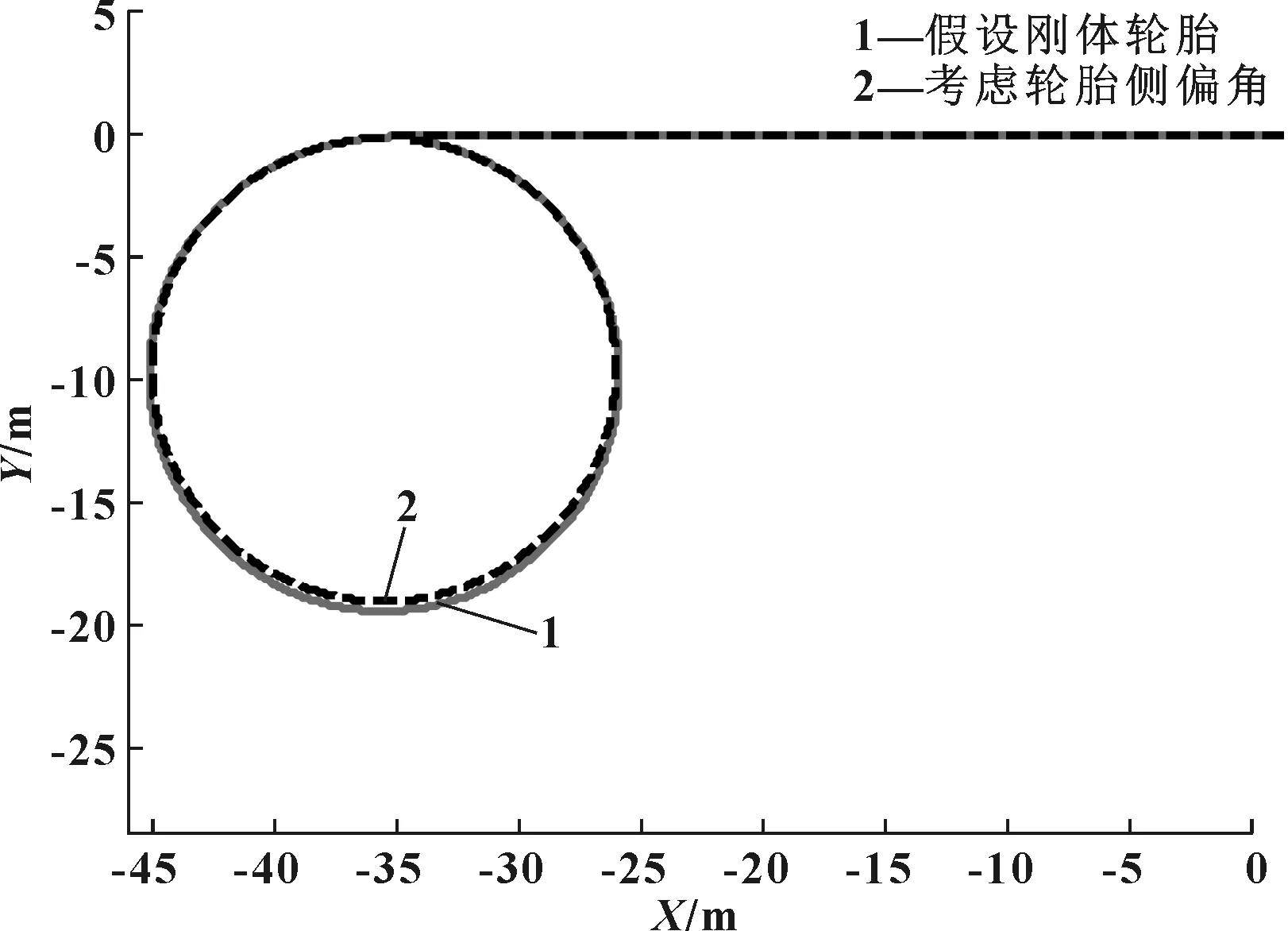
图6 轨迹曲线

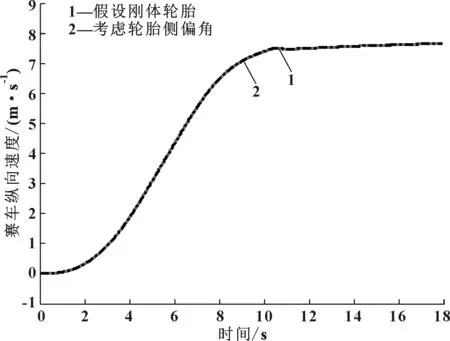
图7 赛车纵向速度曲线

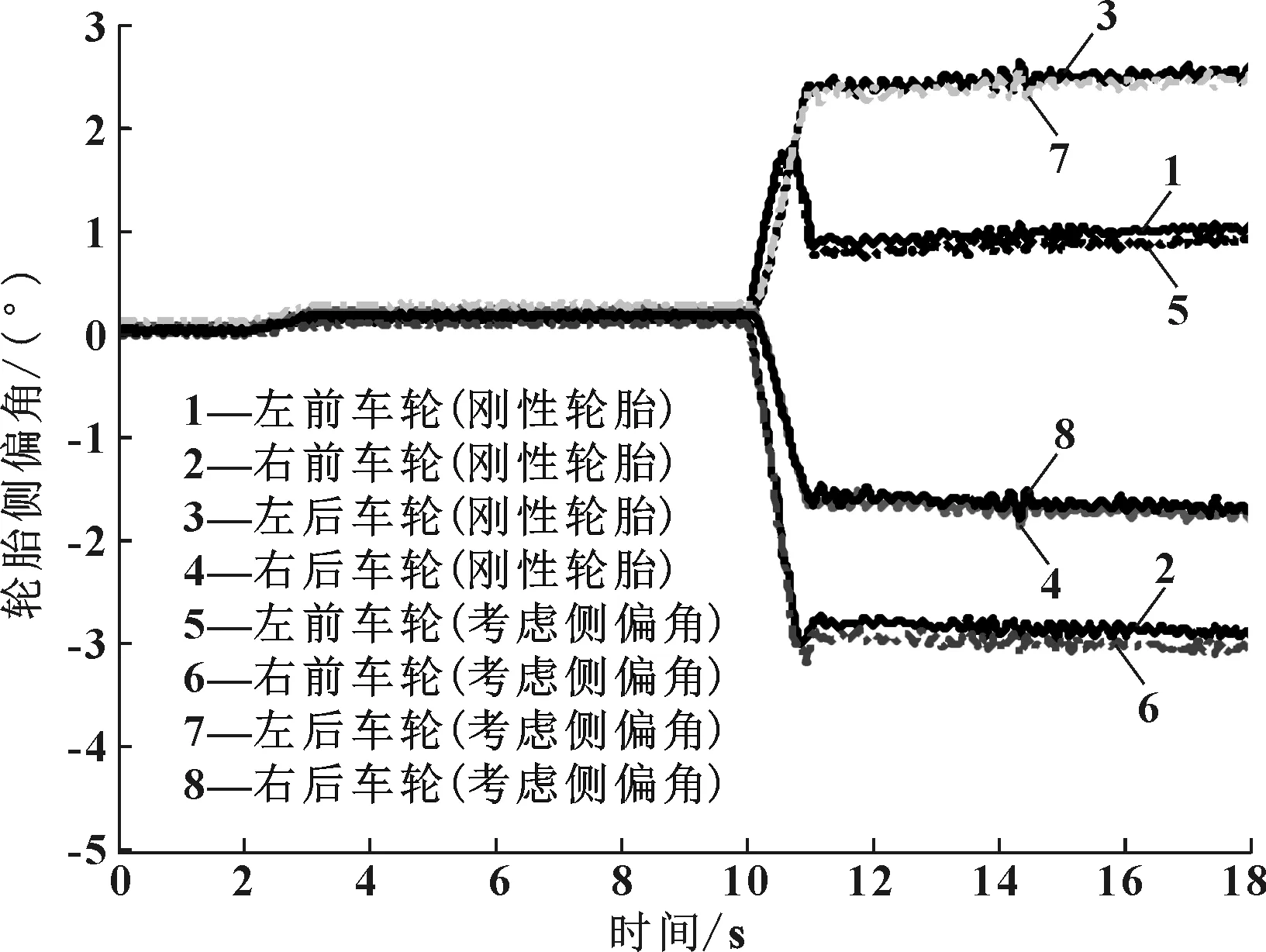
图8 轮胎侧偏角变化曲线

4 结论

考虑轮胎侧偏角的阿克曼转向梯形能使外侧车轮获得更大的转角响应，即减小赛车转弯半径，在弯道中具有更优异转向灵活性和动态响应，因此在赛车阿克曼转向梯形的优化设计中应当充分考虑轮胎侧偏角的影响；此外，基于遗传算法优化后的转向梯形与理想的阿克曼转向模型符合度很高，有效地缩短了赛车转向系统的开发周期。