二分查找判定树的RHC构造法*
徐有为,张宏军,程 恺,陈裕田,周彬彬
(陆军工程大学 指挥控制工程学院,江苏 南京 210000)
0 引言
二分查找又称为折半查找[1],是实现有序表查找的一个非常高效的算法。在对二分查找进行时间复杂性分析和评价时,应用判定树这一工具可以使分析更加科学、形象、直观。然而在结点总数发生变化的情况下,判定树树形也会相应地发生改变。通过分析二分查找算法,本文旨在解决以下两个问题:对于不同结点总数的判定树树形,其结构特点是否具有一般性的规律?针对这一规律,将如何构造判定树,是否存在一个快速并且通用的构造方法?
1 二分查找判定树
二分查找是“基于计算中值地址的”,其原理[2]是:将数组中间位置记录的数据与待查找数据K比较,若两者相等,则查找成功,否则利用中间位置元素将数组分成前后两个子数组,如果中间位置数据大于待查找数据,则进一步查找前一子数组,否则进一步查找后一子数组,重复以上过程,直到找到带查找数据或者查找区间长度为0(即查找不成功)为止。
二分查找由于其高效的平均运算性能,已经广泛应用于计算机科学、通信工程、电子科学等多个学科,其在中文信息处理、中文分词方法[3]、路由查找算法[4]等多个领域的应用均大大降低了传统算法的时间复杂度,取得了满意的结果。二分查找的折半思想也为多目标线性规划寻找近似解[5]、支持向量机分类[6]、最长前缀匹配算法[7]提供了非常高效的解决思路。
以判断选择为主要操作的算法,其流程可以表示成一棵树,称为算法的判定树。判定树由钟鸣等人[8]首次使用,并逐渐广泛应用于算法效率分析中。二分查找判定树是判定树的一种典型应用:把当前查找区间中间位置的结点作为根,左子表和右子表中的结点分别作为根的左子树和右子树。由此得到的二叉树,称为二分查找判定树(Decision Tree)或比较树(Comparison Tree)[9-10]。二分查找判定树是对有序表数据结构很直观形象的表达,便于访问查找。
结点数为13的二分查找判定树如图1所示。

图1 二分查找判定树示意图
判定树传统的构造方法是依照二分查找算法的流程,逐步构造的,需要依次确定根结点位置的元素、缩小范围递归地对左子表进行操作并确定根、缩小范围递归地对右子表进行操作并确定根。图中的每一个结点都代表了一次查找。显然这种面向过程的方法非常复杂,会对有序表的每一个元素都进行比较,尤其当结点数增多时,就显得“耗时耗力”。
李金霞[1]等人提出了一种改进的二分查找判定树构造方法,但是该方法的本质也是一种面向过程的构造方式,同样存在着复杂性的问题。
本文提出的RHC构造方法是面向计算的,有效避免了面向过程构造方法的复杂性,做到迅速准确。为了更好地说明RHC构造法,首先给出倾斜二叉树的定义。
2 倾斜二叉树
2.1 相关定义
定义1(平衡因子):对于二叉树的结点v,其右子树的所有结点个数NR与左子树的所有结点个数NL之差(NR-NL)称为v的平衡因子。
定义2(倾斜二叉树):具有n(n≥1)个结点的二叉树,如果满足,对任意结点v,v的平衡因子等于0或者1,即右子树的结点个数或者比其左子树的结点个数多1,或者与其左子树的结点个数相等,那么称这样的二叉树为倾斜二叉树。
根据定义,对图2所示树形进行判断,显然图(a)是一棵倾斜二叉树,因为所有的结点都满足平衡因子等于0或者1,图(b)不是一棵倾斜二叉树,尽管结点b、c、d、e的平衡因子均等于0,但是a结点的平衡因子等于2,不符合倾斜二叉树的要求。

图2 倾斜二叉树示意图
2.2 构造——开关法
下面给出倾斜二叉树的一种构造方式,结合了面向过程的思想,称为开关法(Switch Method)。假设初态时树为空(即树有0个结点),一共有n个小球,按顺序依次完成进树的过程。每个小球进树到不能进为止(即碰到空结点时停止进树),并在该空结点处填补形成新的结点,比如第一个小球进树填补后成为根结点,以此类推;每个小球变成结点的同时就在对应的结点位置生成出一个开关,开关一共有左右两个状态,用来判定当后续球经过时应该向左走还是向右走,新生成的开关初始状态为右;每有一个小球经过一个开关,该开关的状态发生一次改变。具体构造过程如图3所示。
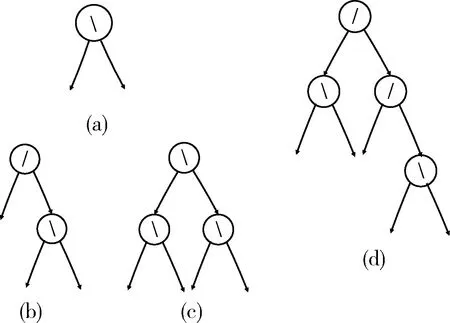
图3 倾斜二叉树的构造示意图
如图3(a)所示,第一个小球进树,变成根结点,生成开关,初始状态向右。图3(b)中,第二个小球进树,遇到第一个开关向右,相应的开关状态变为向左。小球不能再进,变成新的结点,成为根结点的右儿子,生成新的开关,初始状态向右。图3(c)中,第三个小球进树,遇到第一个开关向左,相应的开关状态变为向右,小球不能再进,形成新的结点,成为根结点的左儿子,生成新的开关,初始状态向右。图3(d)中,第四个小球进树,遇到第一个开关向右,相应的开关状态变为向左,遇到第二个开关向右,相应的开关状态变为向左,小球不能再进,形成新的结点和开关,开关初始状态向右。
当所有的小球都完成进树时,就构造出了一棵结点数为n的倾斜二叉树。因为针对单个结点v,凡是经过结点v的小球,都是按照右、左、右、左的顺序进入其子树的,所以对于每个结点v,其平衡因子或者等于1,或者等于0,符合倾斜二叉树的定义。
2.3 性质探究
由倾斜二叉树的定义和构造法,很容易给出以下性质:
性质1:结点数为n的倾斜二叉树树形唯一。
证明采用第二数学归纳法,对n进行归纳。
当n=1或n=2时,结论显然成立,其树形如图3(a)和图3(b)。
假设结论对n≤k均成立,那么当n=k+1时,对n进行奇偶讨论分析。
若n为偶数,令n=2p,由倾斜二叉树的定义可得:根结点的左子树有p-1个结点,右子树有p个结点。因为p-1和p均小于等于k,由归纳假设知,它们的树形是唯一的,所以这种假设下,结点总数为n的树形也是唯一的。
若n为奇数,令n=2p+1,由倾斜二叉树的定义可得:根结点的左、右子树均有p个结点,同理可得此时结点总数为n的树形是唯一的。
故结论对任意的n都成立,证明完毕。
性质1建立了倾斜二叉树与二分查找判定树之间的一一对应关系,确保了两者构造的等价性,是进行后续性质推导的前提。
性质2:倾斜二叉树的左子树、右子树也为倾斜二叉树。
性质3:对于结点数为n的倾斜二叉树,树高为k,其中:k=log2(n+1),为上取整函数。
证明:采用第二数学归纳法,对n进行归纳,
当n=1或n=2时,结论显然成立。
假设结论对n≤k均成立,那么当n=k+1时,对n进行奇偶讨论分析。
若n为偶数,令n=2p,由倾斜二叉树的定义可得:根结点的左子树有个结点,右子树有p个结点,因为p-1和p均小于等于k,由归纳假设知,左子树树高为k1=log2(p),右子树树高为k2=log2(p+1),所以整个树高为log2(p+1)+1,只需证log2(p+1)+1=log2(2p+1),而k2-1 性质4:若n是形如2m-1(m为正整数)的整数,那么结点总数为n的倾斜二叉树是满二叉树。 证明:利用性质二可得,此时树高为m,而树高为m的二叉树结点总数不超过2m-1,当且仅当二叉树为满二叉树时取等,故结点总数为n的倾斜二叉树是满二叉树,证毕。 性质5:对于任意的n,k=log2(n+1),结点总数为n的倾斜二叉树的前k-1层,一定为满二叉树。 证明:同样对n采用第二数学归纳法: 当n=1或n=2时,结论显然成立。 假设结论对n≤k的情况成立,那么当n=k+1时,对n进行奇偶讨论分析。 若n为偶数,令n=2p,由倾斜二叉树的定义可得:根结点的左子树有p-1个结点,右子树有p个结点,由性质2知,左子树树高为k1=log2(p),右子树树高为k2=log2(p+1),因为p-1和p均小于等于k,由归纳假设知,左子树前k1-1层为满二叉树,右子树前k2-1层为满二叉树。若k1=k2,则结论显然成立;若k2=k1+1,则p=2k1,由性质3知,左子树前k1层为满二叉树,结论同样成立。 若n为奇数,同理可证,故结论对任意的n均成立,证毕。 性质2~5简化了对二分查找判定树树形的判断流程,仅仅需要判断底层结点(即叶子结点)的放置顺序而不需要判断整棵树,进一步说明了二分查找判定树与完全二叉树在性质上的相似性。 性质6:如果结点v的平衡因子等于0,那么结点v的左、右子树树形完全一致。 由于结点v的平衡因子等于0,因此结点v的左、右子树结点数相等。根据性质1结点数与树形之间的一一对应关系,故左、右子树树形完全一致。 在给出性质7之前,先定义逆向哈夫曼编码(Reverse Huffman Coding,RHC)。 定义3(逆向哈弗曼编码):对倾斜二叉树上的每条边附上编号,左枝编号为0,右枝编号为1。模仿哈弗曼编码的形式,对第k层上的每个结点,按照从结点到根的路径顺序得到一个二进制编码序列,该序列称为该结点的逆向哈弗曼编码。 图4为一棵逆向哈弗曼编码树,其中第三层上结点的逆向哈弗曼编码依次为(00)2、(10)2、(01)2、(11)2。依照逆向哈弗曼编码的构造特征,可以得到性质7所述的结点放置顺序。 图4 逆向哈弗曼编码树 性质7:如果对倾斜二叉树的第k层的每个结点进行RHC编码,且将第k层的结点按照编码值由大到小的顺序排列,那么第k层的结点一定是由排序序列中前n-2k-1+1个结点构成。 证明:对层数k应用数学归纳法。 当k=2时,显然此结论成立。 假设当k=m时,结论也成立, 那么,当k=m+1时,由性质2可得:根结点的左右子树各有m层,且均为倾斜二叉树。根据RHC的定义,第m+1层的结点编码共有m位,且最低位(即第m位)编码由根结点的枝节决定,前m-1位编码由左子树或右子树决定。结合开关法的过程,结点按照右、左的顺序依次重复出现在根结点的子树上,故结点编码的第m位一定是按1、0、1、0的顺序重复出现。而由归纳假设:前m-1位满足由大到小的顺序,且根据性质6,左、右子树对称一致,所以对于整个m位的逆哈弗曼编码,结点符合编码值由大到小的顺序出现。因此结论成立。 例如:当n=5时,需要在第三层上取两个结点,那么按照编码值排序,应分别取编码为(11)2和(10)2的结点,如图4所示,图中灰色圆形表示第三层上应该包含的结点。 性质6和7,借助二进制哈弗曼编码,以面向计算的方式确立了底层结点的放置顺序,这是RHC构造法成立的理论基础。 根据以上对倾斜二叉树性质的研究,给出二分查找判定树的RHC构造法,具体步骤如下: 第一步:确定二分查找判定树的层数。由性质3可知,对于结点数为n的倾斜二叉树,树高k满足k=log2(n+1)。 第二步:根据性质5,二分查找判定树前k-1层是一棵满二叉树,将前k-1层结点取满。 第三步:对第k层结点按照RHC规则编码,分别计算对应的编码值,将编码值按照从大到小的顺序排列,由性质6,取排序序列中前n-2k-1+1个结点。 第四步:填入关键字,使得中序遍历该树为递增(或递减)序列。 如果结点数增加,不必重新构造该判定树,只要按照如上规则增加一个结点,然后重新填入关键字,使其中序遍历为递增(或递减)序列即可。 至此长度为n的有序顺序表进行二分查找时的判定树构造完成。 下面以结点总数13为例,给出RHC构造法的演示。 第一步:确定树高k,k=log2(n+1)=log214=4; 第二步:前k-1层,即前3层取满; 第三步:对第k层编码,如图5所示,取前n-2k-1+1=6个点; 第四步:按照中序序列填数,最终填数后得到的结果如图6所示。 图5 逆向哈弗曼编码图 图6 结点数为13的二分查找判定树 中序序列填数完成后可以做一个投影,在树形规则的前提下,可以发现投影是一个递增的序列,并把数轴分成了14个区域。 评估构造法效率最直接的方式,是计算使用该构造法需要耗用多少时间。于是,假设一次运算耗时一个单位时间,便将效率分析问题转换为统计运算次数问题。 传统面向过程(Process-oriented)的构造法需要对二分查找判定树上的每个结点运算三次,分别是计算左边界下标、右边界下标和“中值”点下标。因此,对于结点总数为n的二分查找判定树,面向过程构造法需要耗时TP-o(n)=3×n。RHC构造法利用逆向哈弗曼编码和二分查找判定树的中序有序性,只需针对二分查找判定树最底层的结点计算编码值,每个底层结点只运算一次,所以,对于结点总数为n的二分查找判定树,总耗时TC-o(n)满足TC-o(n)=2k-1,其中k表示二分查找判定树的树高,k=log2(n+1)。 根据上述的耗用时间表达式,分别绘制出运算耗费时间随结点数变化的趋势图,如图7所示。 图7 效率对比 从图7中可以看出,面向过程的构造法对应了一条直线,其耗用时间与结点总数呈线性关系。RHC构造法是一个分段函数,运算时间与树高有关。通过比较分析,相较于传统构造法,RHC构造法存在明显的优越性,并且当结点总数增加时,这种优越性更加明显。 另外,当结点总数为n的二分查找判定树树形已知,需要新增一个结点时,面向过程的构造法必须重新构造整个二分查找判定树,因为面向过程的构造法不具有可重复性,由前面的分析可知,这种情况,传统方法需要的时间复杂度是O(n),而RHC构造法只需要在原有树形的基础上额外进行一次运算,该方法对应的时间复杂度是O(1),这大大提高了构造效率。 本文定义的倾斜二叉树实用性强,具有很好的平衡性和单向倾斜性,基于倾斜二叉树性质提出的RHC构造法是一种面向计算的构造法,经对比验证,比传统面向过程的构造法更高效、迅速、准确。该方法对于同类的采用分治方法进行问题求解的算法分析具有借鉴意义。
3 RHC构造法


4 性能分析

5 结束语

