适时补白,丰富教学
——“需要多少钱”教学实践与思考
□ 赖要万
理解乘法的算法和算理是乘除法知识学习的重点,也是难点。“需要多少钱”是北师大版三年级上册第四单元的教学内容,这节课主要学习两位数乘一位数、乘积在百以内的口算乘法,它是学习笔算乘法的基础。通过本节课的学习,让学生经历计算两位数乘一位数的思考与交流的过程,理解两位数乘一位数的乘法意义,探索并掌握两位数乘一位数的口算方法,理解乘法的算理,体验算法多样化,达到用乘法知识解决简单的实际问题的能力,感受数学与生活的密切联系。
“需要多少钱”呈现了一幅海边游泳用品商店的情境图,图上有各种游泳用品的名称和价格。教材首先借助人民币这一实物模型,沟通了实物模型与算法之间的联系;然后引入“点子图”和“表格”两个工具来进行乘法的直观运算,让学生理解笔算乘法的算法。当学生理解了乘法算理,就能逐步脱离对直观的依赖,直接运用算法进行两位数乘一位数的口算,达到算法运算的阶段。
但是,教材只给我们呈现了浅显直观的内容,远不够作为教师课堂传授给学生的全部内容。教师如果能在课堂教学的各个环节中,对教材内容、学生思维的空白处,适时地补白、延伸,将使得课堂教学丰富多彩,饱满而有张力。
一、重构示图,揭示算理
数学源于生活,生活中处处有数学。教学中,如果能密切联系生活实际,贴近学生生活,寻找生活中的数学素材,将学生熟悉的蕴含着数学知识的生活实例引进课堂,就能拉近学生与数学知识之间的距离,从而激发学生的求知欲望,增强其学习数学的主动性。教材正是在这种情境下,出示第一个问题:“买3个泳圈需要多少元?说说你是怎样想的。”
教材呈现两种解决方法:一种是借助已经学过的加法,通过连加“12+12+12”来得出结果;一种是借助人民币模型,得出“10×3=30”,“2×3=6”,“30+6=36”。

教材把这两种解法分开呈现,教师如果只是照着书上这样来教,未免太肤浅,没有抓住两种算法之间的联系。其实教师如能引导学生对两种方法进行深入观察,就能发现加法和乘法之间的联系,如下图所示:

这样,通过生活中熟悉的人民币模型,让学生初步感受乘法算理,体会位值原理,直观易懂,学生在不知不觉中掌握了两位数乘一位数不进位口算的计算方法。
二、设问补白,理解算法
利用贴近学生生活实际的直观模型,初步掌握“12×3”的算法。对小学生来说只是第一步,如何把生活中的直观模型,抽象成符号,进一步深入理解其中原理,是教师必须要做的工作。于是,教材出示了第二个问题:“淘气和笑笑是这样算的,你看懂了吗?与同伴说一说。”

教材在这里第一次出现点子图和表格,指导学生看懂淘气和笑笑如何借助这两样工具来进行乘法运算是关键。在左边的图例中,淘气把“12×3”的点阵平均分成两部分,使之可以用表内乘法分别算出两部分结果,再用加法“合”起来得出结果。
这只是抛砖引玉,教师在教学时,应该鼓励学生充分发挥想象,思考多种分解方法,如:

把两位数乘一位数,分解为表内乘法和加法的组合,这种化新知为旧知,是数学“转化”的思想。
除了点子图,教材还出示了格子图这个工具,帮助学生认识两位数乘一位数的算法。把12看成10+2,分别乘3,再把积相加。
教学如果仅仅停留在让学生模仿着圈一圈、填一填、算一算,那就远远没有达到真正的目的。作为教师,应该能够在关键处进行适时补白,引导学生观察思考:填表格计算的原理是什么?它有什么作用?还可以进行怎样转换?
小结时,让学生思考:淘气和笑笑所用的两种不同的算法有什么异同点?让学生明白,原来点子图和表格式的算法也有相通之处!
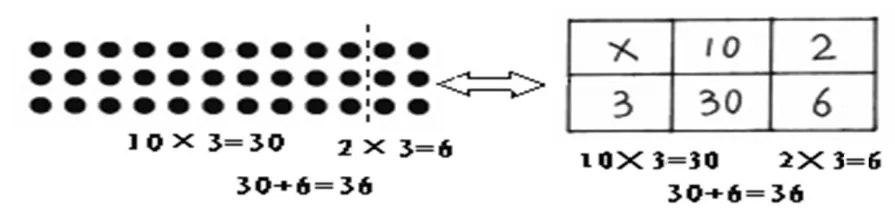
在学生充分交流、讨论的基础上,教师及时小结两种算法共同点:把一个整体“分块”求积,再求各个积的和。
三、横联纵合,融会贯通
不管是借助直观模型、抽象符号,对算法进行直观展示,还是对算理进行深入剖析,教师的教学都是块状的、碎片化的,学生学习的知识是孤立的、点状的。如何让这些孤立的、点状的知识,融入学生的知识结构中,就需要教师适时点拨,横联纵合,找到沟通知识的纽带,使学生恍然大悟,醍醐灌顶。
因此,教学进行到这里时,教师应当适时地对刚才各个环节进行梳理回顾,通过一个个的“”,把各个知识点打通,讲清算法,理清算理,融会贯通,同时,又呼应了课题“需要多少钱”。
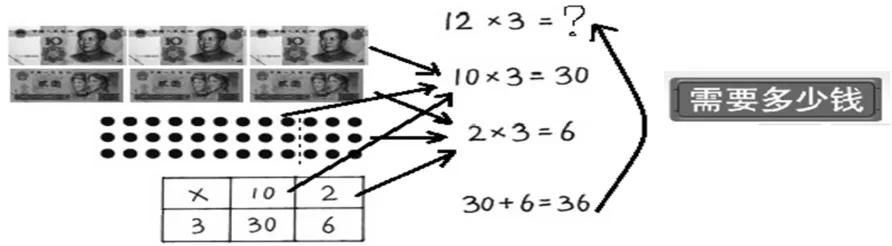
至此,学生头脑中的“?”会变成“!”。对于进入下一阶段“小皮艇的价钱是皮球的4倍,求一只小皮艇多少元?”的巩固练习,也就水到渠成了。
教材是静态的,是通过几幅图、几个问题串,来表达编者的很多意图,这就需要教师读懂文本背后所蕴含的丰富信息,在教材“空白”处适时地补白,适当地延伸,让课堂教学丰富起来。

