随机需求多目标连续均衡网络设计

方文彬，王涛，黄汝晴，黄中祥，曾铃

随机需求多目标连续均衡网络设计

方文彬1，王涛2，黄汝晴2，黄中祥1，曾铃1

(1. 长沙理工大学 交通运输工程学院，湖南 长沙，410004；2. 中南大学 交通运输工程学院，湖南 长沙，410075)

为考察多目标特性以及需求不确定性对网络设计的影响，假设OD(origin destination)需求服从双侧截尾正态分布，构建多目标连续均衡网络设计的双层规划模型。上层规划以系统出行时间的期望最小、路网服务水平可靠性最大和投资预算最小为目标，下层规划采用用户均衡分配刻画出行者路径选择行为。给出基于蒙特卡洛仿真的多目标遗传求解算法，采用测试网络验证模型和算法的有效性。研究结果表明：采用多目标连续均衡网络设计模型可以获得多个非劣解供决策者选择；不同目标之间存在明显的相关关系，尤其是投资手段存在明显的边际递减效应，宜结合交通管理措施共同使用。

连续均衡网络设计；多目标规划；双层规划；服务水平可靠性；第二代非支配排序遗传算法

路网设计是指在给定的约束条件下，通过新建道路或改扩建现有路段，使网络的某种性能指标达到最优，包括离散、连续和混合网络设计3种类型[1]。自ABDULAAL等[2]提出连续均衡网络设计模型以来，国内外学者对网络设计问题开展了深入研究，取得了丰富的研究成果[3]，并形成了以双层规划为代表的研究方法。然而，传统网络设计很少考虑交通系统的不确定性，所获得的路网设计方案鲁棒性较差。近年来，随着对道路网络可靠性研究的不断深入，人们逐步认识到不确定性是交通系统的本质特性之一[4]，要获得更加符合实际的网络设计方案，就必须在网络设计过程中考虑交通系统的不确定性。目前，人们在随机供给和(或)随机需求影响下的交通网络设计方面进行了研究，如：许良等[5]从路段容量的随机变动出发，以概率用户均衡为基础研究了基于路段能力可靠性的交通网络设计；SUMALEE等[6]提出了随机需求下以出行时间可靠性为目标的网络设计模型；CHOOTINAN等[7]在交通需求不确定条件下将容量可靠性引入城市交通网络设计中，建立了基于Probit随机用户均衡的连续网络设计模型；陆化普等[8−9]从发生和吸引交通量的不确定、OD(origin destination)需求的不确定2个方面考察了不确定需求下的离散交通网络设计问题；蒲云等[10]采用部分随机用户均衡模型描述了事故影响下的路网状态，建立了以期望社会成本最小为目标的可靠网络设计模型。CHEN等[11]归纳了不确定需求下的随机网络设计方法，提出了期望值模型、约束机会模型和相关机会模型这3种建模方法。但现有关于不确定环境下的网络设计研究多假定路段容量或交通需求服从正态分布或均匀分布，这些概率分布能否真实、合理地刻画供求的随机性特征还缺乏必要的论证。另一方面，现有关于网络设计的研究多局限于系统总阻抗最小或时间可靠性最大等单一目标。然而，交通规划管理部门对未来的网络除要求其阻抗小之外，还要求网络的运行效率高、建设成本低、承载能力大以及网络能应对较高风险等诸多目标。XU等[12]建立了以系统出行时间与投资预算之和最小为目标的网络设计模型；YIN[13]则以出行时间最小和网络效益最大为目标构建网络设计模型。上述研究虽然考虑了网络设计的多目标特性，但在建模环节常将多目标问题转化为单目标问题求解。事实上，在不确定环境下同时优化多个目标的网络设计更加符合实际，能够满足决策者对未来网络的多种需求，目前该领域的研究成果偏少。CHEN等[14]构建了同时优化容量可靠性和出行时间可靠性的连续均衡交通网络设计模型，陆化普等[15]假设供求随机变化，通过引进风险价值理论建立了考虑决策者风险态度的多目标双层规划模型。为更真实地描述实际问题，本文作者假定交通需求服从双侧截尾正态分布，以服务水平可靠性最大、系统总阻抗和投资预算最小为目标构建随机需求作用下的多目标连续均衡网络设计模型，设计基于蒙特卡洛仿真的多目标遗传求解算法，最后用算例验证该网络设计模型的特性。

1 多目标连续均衡网络设计建模

1.1 交通需求随机性刻画

1.2 网络设计的优化目标分析

一般地，交通系统管理部门总是希望用最少的投资来获得效率最高的网络，同时还要求规划路网能应对一定风险。为此，本文在构建考虑需求随机性的多目标网络设计模型时，主要从交通系统运行效率、路网服务水平可靠性和资金投入量3方面构建网络设计模型的优化目标。

从交通系统运行效率的角度考虑，运行效率越高的路网其总阻抗越小，因此，该目标可以采用系统总阻抗的期望最小化来描述：

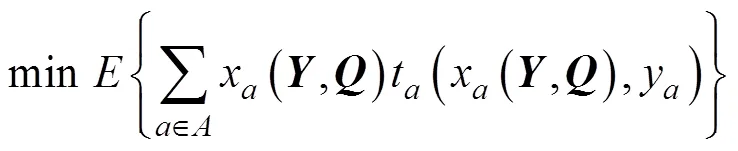
式中：x为路段上的交通量("Î)；y为路段的容量增加值；=(1, …, y, …,|A|)为路段容量增加值向量，||为路段数量；=(1, …, Q, …,|W|)为OD需求向量，||为OD对数量；t(×)为路段的走行时间；(×)表示取均值。本文采用BPR(bureau of public roads)函数作为路段走行时间函数：

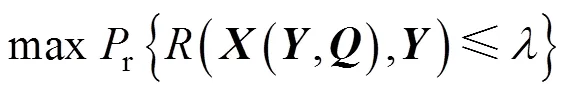
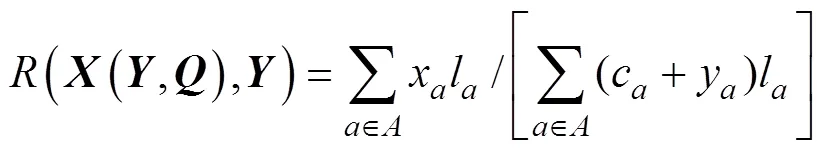
式中：r为概率；=(1, …, x, …,|A|)为路段流向量；为某一指定的饱和度阈值；(×)为路网饱和度；l为路段的长度。

通常1个城市用于交通基础设施建设的资金是有限的，网络设计过程中应尽可能用较小投资来获得较大效益。为此，本文将投资费用最小化也作为网络设计模型的优化目标之一，该目标可表示为

式中：G(×)为投资函数，

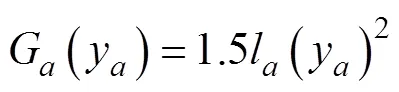
1.3 随机需求多目标连续均衡网络设计模型

网络设计问题是一个典型的“领导者—追随者”问题，通常用双层规划来刻画，其中上层决策者为系统管理者，下层决策者为道路用户。根据前述分析，以系统总阻抗、路网服务水平不可靠性以及投资费用最小作为上层优化目标，上层决策变量为路段容量的增加值。系统管理者对路网的改善会影响道路用户的路径选择行为，出行者会随着网络结构的改变及时调整其路径选择，以确保个体出行费用最小，为此，采用用户均衡来描述下层出行者的路径选择。

随机需求作用下的多目标连续均衡网络设计可以构建成如下数学规划模型。

上层规划：

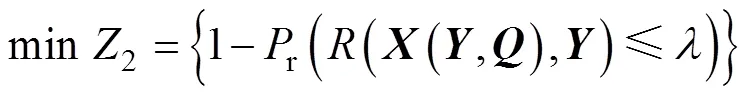
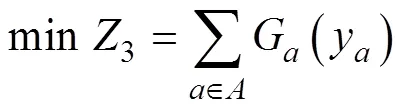
下层规划：

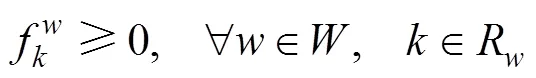
2 模型求解算法

在多目标优化问题中，有多个目标函数需要同时优化。由于目标之间无法比较，甚至存在冲突，最终将导致不一定存在同时满足所有目标的最优解。多目标优化问题通常存在1个解集，其特点是与解集之外的任何解相比，它们至少有1个目标函数比解集之外的解好而其他目标函数又不比解集之外的解差，这种解称为非支配解或Pareto最优解。求解多目标优化问题时，NSGA-Ⅱ算法是被应用得最广泛的算法之一。NSGA-Ⅱ通过非支配排序技术寻找最接近真实Pareto前沿的解；拥挤度用来确保非支配解的多样性，包含最优父代解与最优当前解的精英化策略，增强了算法的收敛性，其具有现代智能优化算法的优点，鲁棒性好，计算高效[16]。以NSGA-Ⅱ算法为基础，结合蒙特卡洛仿真技术，给出求解随机需求条件下多目标连续均衡网络设计模型的算法步骤如下。

步骤1 初始化。定义遗传算法的基本参数，包括编码方式、种群大小、适应度函数和交叉、变异概率以及最大迭代次数。给定OD需求样本规模S，随机生成1个父代种群。在上层模型约束条件对应的搜索空间内随机生成足够可信的个体，令进化代数=1。

步骤2 随机抽样及路段流量分配。

步骤2.1 采用蒙特卡洛仿真方法进行需求抽样，并且对每个OD需求方案采用Frank-Wolfe算法求解下层用户均衡配流模型，得到每个个体对应的路段流量。

步骤2.2 将各路段流量代入上层模型，计算适应度。

步骤3 采用NSGA-Ⅱ更新种群。

步骤3.1 将所有个体按非支配关系排序，令适应度等于非支配序rank。

步骤3.2 选择、交叉、变异生成1个子代种群Q，大小为。

步骤4 迭代。

步骤4.1 将第代产生的新种群Q与父代P合并成R，大小为2。

步骤4.2 对R进行快速非支配排序，产生一系列非支配集F。

步骤4.3 计算F中每个个体的拥挤度。

步骤4.4 将F放入新的父代种群P+1，直到P+1超过，其最后的非支配集为F。

步骤4.5 对F中的个体按照拥挤度算子排序，取前(−|P+1|)个个体，使P+1个体数量达到。

步骤4.6 通过遗传算子(选择、交叉、变异)产生新的子代种群Q+1。

步骤5 判断是否达到最大进化代数，若不是，则返回上述操作步骤2，同时令=+1；若是，则算法结束，输出Pareto最优解。

该算法的具体流程如图1所示。

3 算例

算例网络如图2所示。该网络由9个节点和12条单向路段组成。图2中线上数字为各路段编号。假定只有1个OD对，从节点A到节点I。测试网络各路段的长度、路段自由流时间、路段现状通行能力以及路段容量增加值的上限等特性参数的取值设置如表1所示。

设OD对AI之间的需求均值为3 000辆/h，需求下限为2 000辆/h，上限为4 000辆/h，需求的均方差设为均值的0.3倍。为确保抽样精度，设抽样次数为 1 000。遗传算法的主要参数设置如下：种群规模为100，最大代数为100，个体采用二进制编码，交叉概率为0.8，变异概率为0.01。BPR函数的参数=0.15，=4，路网饱和度阈值取为=0.85。在上述参数下，运用本文建立的模型和算法求解算例网络，获得随机需求作用下考虑多目标的连续均衡网络设计模型的Pareto最优解如图3所示(其中，以投资预算、系统出行时间的期望值和路网饱和度小于0.85的概率为坐标轴)。

图3表明：Pareto最优解由36个非劣解组成，表明当出行时间期望值增大时，交通拥堵加剧，路网服务水平可靠性逐渐下降，路网出行条件变差。受需求随机性的影响，Pareto最优解在图中的分布不是特别集中，但在一定程度上仍回归于1个曲面；每个点均代表了1种路段容量改善方案，这与单目标网络设计只能获得某一确定的最优解有明显不同。在多目标作用下，系统管理者在权衡总出行时间、服务水平可靠性和投资预算多个目标后，可以获得多样化的路段容量改善方案并可根据实际需要选取某一种方案进行实施，这有效地提高了网络设计的弹性。系统总阻抗的期望、服务水平可靠性与投资预算这3个目标两两之间的Pareto最优解见图4。

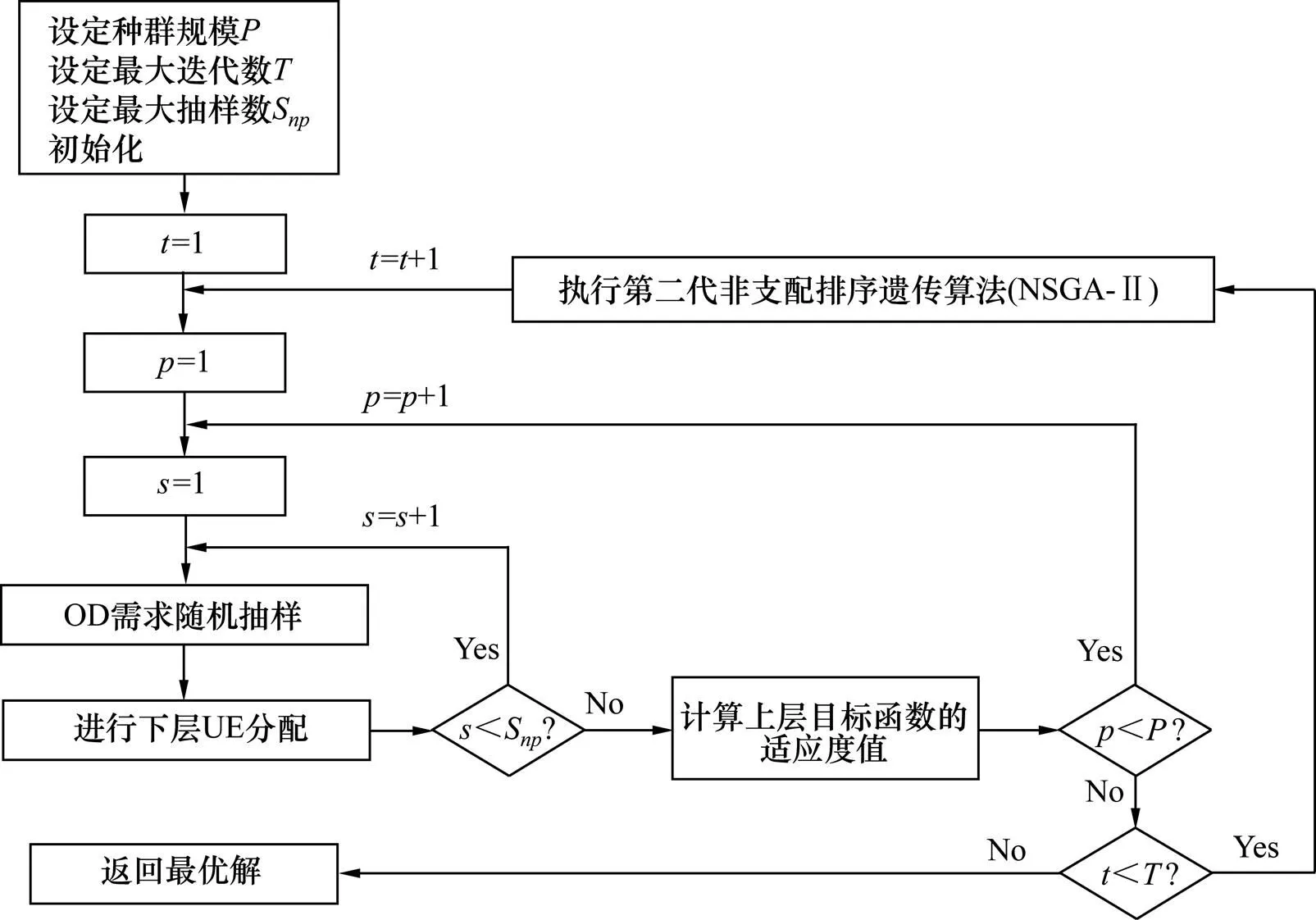
图1 算法流程

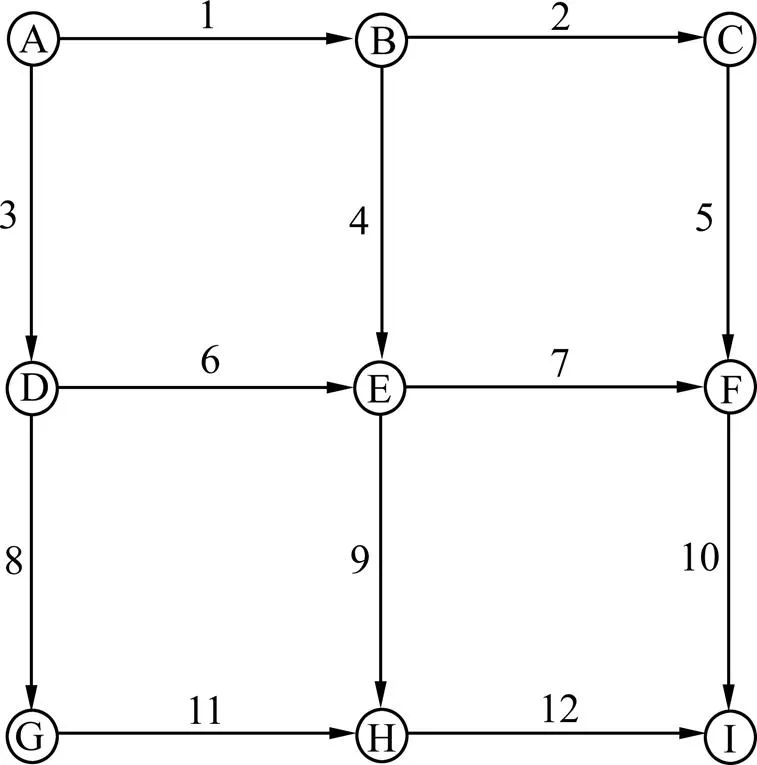
图2 算例网络

表1 路段特性参数

从图4(a)可见：系统出行时间的期望值与服务水平可靠性之间存在着相关关系；随着系统出行时间期望值增加，路网饱和度小于0.85的概率逐渐减少。

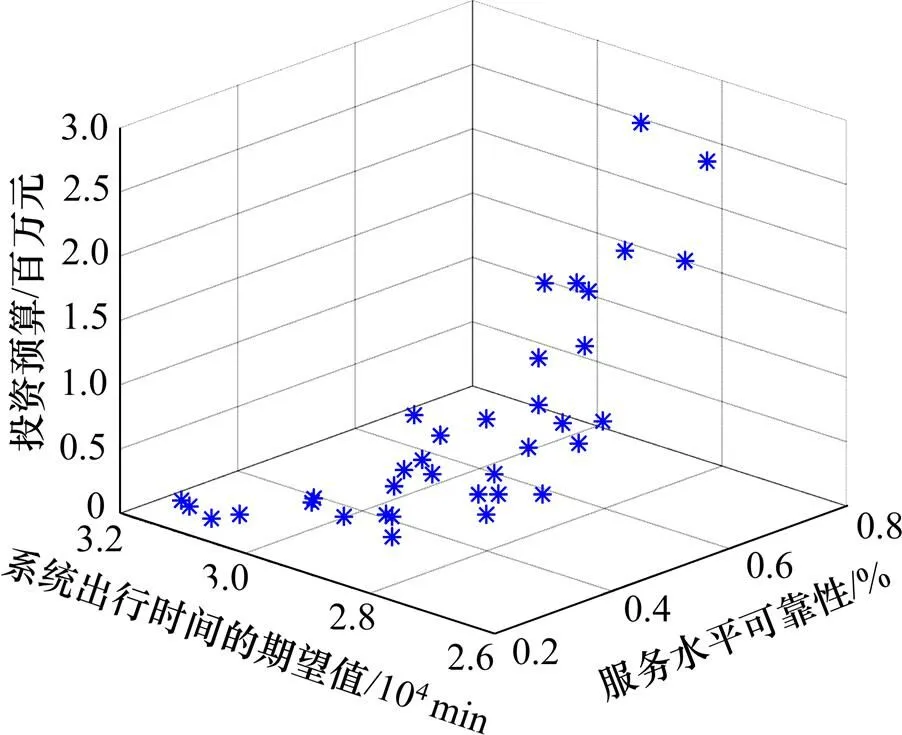
图3 多目标双层规划模型的Pareto最优解

(a) 服务水平可靠性与系统出行时间期望值的关系；(b) 服务水平可靠性与投资预算的关系；(c) 系统出行时间期望值与投资预算的关系

从图4(b)可见：随着投资预算增加，网络饱和度小于0.85的概率逐渐增加，但可靠性增加的幅度不断变小并趋于平缓。这说明路网服务水平可靠性随投资预算的增大而增大，且单位资金投入对网络服务水平可靠性的提高逐渐减少，呈现出边际递减效应。

单位资金投入的边际效应递减现象在投资预算和系统出行时间的期望值之间更明显，如图4 (c)所示。前期投资使得系统出行时间的期望值明显下降，而投资进一步增加对出行时间期望值的影响明显减弱。这表明单位投资在网络设计的前期作用较明显，后期效果逐渐减弱。

4 结论

1) 网络设计本质上是1个多目标规划问题。与单目标网络设计相比，本文提出的方法在对多个目标进行综合衡量后，可以给出多样化的决策方案。

2) 系统总阻抗与服务水平可靠性及系统总阻抗与投资预算之间均存在负相关关系，而投资预算与服务水平可靠性之间存在着正相关关系。

3) 增加预算能够减少系统出行时间和增加路网服务水平可靠性，但其存在明显的边际递减效应，不能作为缓解拥堵和提高交通系统运行效率的一种长期有效措施。

[1] 高自友, 张好智, 孙会君. 城市交通网络设计问题中双层规划模型、方法及应用[J]. 交通运输系统工程与信息, 2004, 4(1): 35−44. GAO Ziyou, ZHANG Haozhi, SUN Huijun. Bi-level programming models, approaches and applications in urban transportation network design problems[J]. Journal of Transportation Systems Engineering and Information Technology, 2004, 4(1): 35−44.

[2] ABDULAAL M, LEBLANC L J. Continuous equilibrium network design models[J]. Transportation Research Part B: Methodological, 1981, 15(4): 249−266.

[3] 《中国公路学报》编辑部. 中国交通工程学术研究综述·2016[J]. 中国公路学报, 2016, 29(6): 71−77. Editorial Department of China Journal of Highway and Transport. Review on China’s traffic engineering research progress: 2016[J]. China Journal of Highway and Transport, 2016, 29(6): 71−77.

[4] 况爱武, 黄中祥. 随机供求下的道路服务水平可靠性[J]. 系统工程, 2007, 25(6): 25−30. KUANG Aiwu, HUANG Zhongxiang. On the service reliability in stochastic supply and demand[J]. Systems Engineering, 2007, 25(6): 25−30.

[5] 许良, 高自友. 基于路段能力可靠性的城市交通网络设计问题[J]. 中国公路学报, 2006, 19(2): 86−90. XU Liang, GAO Ziyou. Urban transport network design based on link capacity reliability[J]. China Journal of Highway and Transport, 2006, 19(2): 86−90.

[6] SUMALEE A, WATLING D P, NAKAYAMA S. Reliable network design problem: case with uncertain demand and total travel time reliability[J]. Journal of the Transportation Research Record, 2006, 1964(1): 8l−90.

[7] CHOOTINAN P, WONG S C, CHEN A. A reliability-based network design problem[J]. Journal of Advanced Transportation, 2005, 39(3): 247−270.

[8] 陆化普, 蔚欣欣, 卞长志. 发生吸引量不确定的离散交通网络设计模型[J]. 统计与决策, 2011(6): 8−12.LU Huapu, WEI Xinxin, BIAN Changzhi. Discrete traffic network design model under attracting quantity uncertainty[J]. Statistics and Decision, 2011(6): 8−12.

[9] 陆化普, 蔚欣欣, 卞长志. OD需求不确定的离散交通网络设计模型研究[J]. 公路交通科技, 2011, 28(5): 128−132. LU Huapu, WEI Xinxin, BIAN Changzhi. Model and algorithm of discrete network design problem under OD demand uncertainty[J]. Journal of Highway and Transportation Research and Development, 2011, 28(5): 128−132.

[10] 蒲云, 刘海旭. 基于部分随机用户均衡的可靠性网络设计[J]. 西南交通大学学报, 2011, 46(2): 321−325. PU Yun, LIU Haixu. Reliable network design based on partial stochastic user equilibrium[J]. Journal of Southwest Jiaotong University, 2011, 46(2): 321–325.

[11] CHEN A, KIM J Y, LEE S, et al. Models and algorithm for stochastic network designs[J]. Tsinghua Science and Technology, 2009, 14(3): 341−351.

[12] XU Tianze, WEI Heng, WANG Zhuande, et al. Study on continuous network design problem using simulated annealing and genetic algorithm[J]. Expert Systems with Applications, 2009, 36(2): 2735−2741.

[13] YIN Yafeng. Multiobjective bi-level optimization for transportation planning and management problems[J]. Journal of Advanced Transportation, 2002, 36(1): 93−105.

[14] CHEN A, ZHOU Zhong, CHOOTIANA P, et al. Optimizing capacity reliability and travel time reliability in the network design problem[C]// Proceedings of the 12th International Conference of Hong Kong Society for Transportation Studies. Hong Kong, China, 2007: 223−232.

[15] 陆化普, 李锐, 蔚欣欣. 供给与需求不确定的离散交通网络设计模型[J]. 东南大学学报(自然科学版), 2012, 42(6): 1221−1226. LU Huapu, LI Rui, WEI Xinxin. Discrete traffic network design model under supply and demand uncertainty[J]. Journal of Southeast University(Natural Science Edition), 2012, 42(6): 1221−1226.

[16] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi⁃objective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182−197.

(编辑 陈灿华)

Network design of multi-objective continuous equilibrium with stochastic demand

FANG Wenbin1, WANG Tao2, HUANG Ruqing2, HUANG Zhongxiang1, ZENG Ling1

(1. School of Traffic and Transportation Engineering, Changsha University of Science and Technology, Changsha 410004, China;2. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

To investigate the impacts of multi-objective characteristics and the uncertain traffic demands on road network design, a bi-level programming model for the continuous equilibrium network design with multiple objectives was proposed with the assumption that the OD(origin destination) demands followed the bilaterally truncated normal distribution. The upper-model was a multi-objective programming model with the minimum expected network travel time, the maximum reliability of network service level and the minimum investment budget. The lower-level model was a user equilibrium distribution model. A multi-objective genetic algorithm was employed to solve the problem based on the Monte Carlo simulation. A small-scale network was used to demonstrate the validity of the model and the algorithm. The results show that the multi-objective continuous equilibrium network design model can measure some indicators comprehensively, and obtain as many non-inferior solutions as possible for decision makers to choose. There is a clear correlation between the objectives. In particular, the investment has significant marginal diminished effect, and should be used together with traffic management measures.

continuous equilibrium network design; multi-objective programming; bi-level programming; service level reliability; non-dominated sorting genetic algorithm-II

10.11817/j.issn.1672-7207.2018.09.031

U491

A

1672−7207(2018)09−2350−06

2017−10−15；

2017−12−16

国家自然科学基金资助项目(51338002，51208064)；湖南省研究生科研创新项目(CX2015B342) (Projects(51338002, 51208064) supported by the National Natural Science Foundation of China; Project(CX2015B342) supported by the Research and Innovation Program of Graduate Students in Hunan Province)

黄中祥，教授，博士生导师，从事交通运输规划研究；E-mail: mehzx@126.com