强风沙环境下动车组塞拉门预防性维修周期研究
李荧,戚峰,尹鹏飞,葛盛昌,鲁寨军
强风沙环境下动车组塞拉门预防性维修周期研究
李荧1, 2,戚峰3,尹鹏飞3,葛盛昌3,鲁寨军1, 4, 5, 6
(1. 中南大学 交通运输工程学院,湖南 长沙,410075;2. 中国铁路北京局集团有限公司,北京,100860;3. 中国铁路乌鲁木齐局集团有限公司,新疆维吾尔自治区 乌鲁木齐,830011;4. 中南大学 轨道交通安全教育部重点实验室,湖南 长沙,410075;5. 轨道交通安全关键技术国际合作联合实验室,湖南 长沙,410075;6. 轨道交通列车安全保障技术国家地方联合工程研究中心,湖南 长沙,410075)
针对强风沙运用环境与长交路运行工况对动车组关键系统及部件故障的影响特性,建立基于系统可用度的预防性维修周期决策模型;考虑兰新(甘肃兰州—新疆乌鲁木齐)高铁开行时间短、检修经验不足等问题,提出基于Monte−Carlo思想的统计模拟算法。利用兰新客运专线强风沙运用环境下的塞拉门服役故障信息,对决策模型分布函数进行定义、参数估计和假设检验;利用建立的模型在MATLAB环境下仿真计算塞拉门预防性维修周期,结合现场实验验证维修决策模型和算法的有效性。研究结果表明:塞拉门故障服从形状参数为0.779、尺度参数为315 158.178的双参数威布尔分布;随预防性维修周期增加,塞拉门的可用度先增加后减小,考虑到预防性维修的人员组织、均衡作业和修程间隔等因素,确定其维修保养运行里程为10万km。
强风沙;维修周期;动车组;塞拉门;兰新客运专线
兰新(甘肃兰州—新疆乌鲁木齐)高铁长期处于强风沙、高温、高寒、长运行路径等特殊的环境中[1],动车组各系统、部件及整体综合性能面临严峻考验。为了使动车组对特殊运用环境有良好的适应性,一方面,人们针对受环境影响敏感的系统进行合理研发与改造;另一方面,在运用维修上,需结合季节、天气、故障规律等实际因素,制定合理的预防性维修范围和周期,尽可能提前防止故障发生,以保障动车组安全、准时运行和提高乘客满意度。国内外许多学者对复杂设备维修周期进行了大量研究,如吕立波等[2−6]针对非动车组复杂设备,建立了周期决策模型,并提出了相应计算方法。在动车组预防性维修周期方面,丁阳喜等[7]对动车组车轮旋修周期进行了研究;赵泽平等[8]提出了一种基于可靠性来确定预防性维修周期的方法,并以CRH1型动车组高压电气系统为例进行了验证;赵金方等[9−11]针对动车组零部件预防性维修周期进行了研究。目前,人们对考虑环境因素对动车组维修周期的研究较少,为此,本文作者针对兰新高铁强风沙运用环境的实际现状,根据可靠性理论,通过收集、分析动车组目标系统故障数据,建立相应的维修周期决策模型,采用模拟仿真的方法确定预防性维修周期,以便为动车组运用维修部门提供参考依据。
1 维修周期决策模型
兰新高铁于2014年11月开通运营至今,由于人员、时间、技术、设备和动车组自身状态等原因,动车组故障数据和设备检修经验不足,通过动车组运用维修信息和经验来推断预防性维修周期不具备可行性。设备故障的发生具有随机性,针对动车组环境敏感的部件和系统,根据积累的动车组真实服役故障数据,确定系统的故障分布函数,结合相关标准与兰新高铁动车组运用维修实际的可操作性,建立科学合理的运用维修周期决策模型,是确定强风沙地区动车组运用维修周期的重要途径。
1.1 仿真模型定义
动车组故障发生与系统、部件的工作时间有关。工作时间与运行里程密切对应,我国实行以运行里程为主、运行时间为辅的检修制度。设强风沙环境对某系统或系统组件有显著影响,且其故障服从某分布函数,在1个预防性维修周期内(预防性维修周期与预防性维修作业时间之和)发生了多次故障,发生故障后需在动车组运用所进行动车组故障处理,由于动车组件多为模块化设计,故障处理多以更换故障件和清洁保养为主,故障后维修如新;运行途中发生故障时,返所进行故障处理以及预防性维修均会降低动车组的利用率,其耽误的时间和造成的行车影响折算为运行里程。以动车组可用度(1/(1+2),其中,1为工作时间,2为不能工作时间)[12]为目标函数,建立以下最佳周期仿真优化模型。
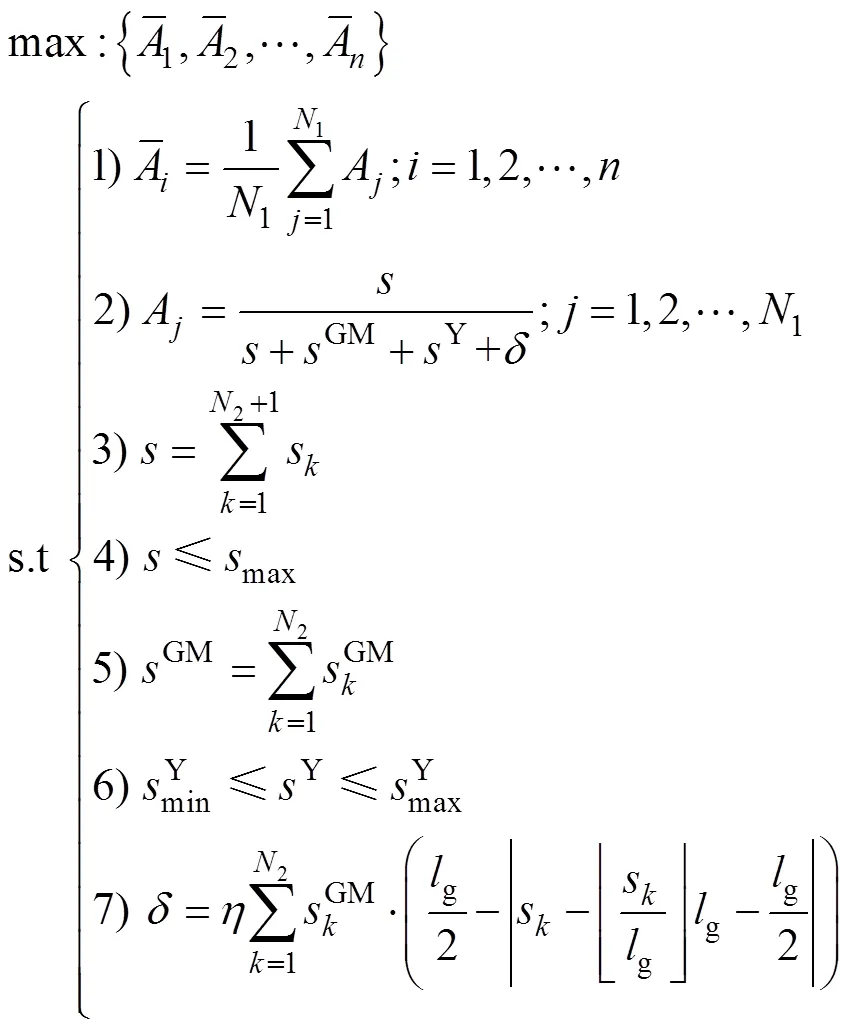
各约束条件含义如下:
约束条件1) 表示平均可用度的计算公式,即1次计算的可用度平均值。
约束条件2) 表示可用度的计算方法,即以上线总运行里程为分子,上线总运行里程、故障修耽误折算的总运行里程、预防性维修耽误折算的运行里程与惩罚函数值的总和为分母的比值。
约束条件3) 表示1个预防性维修周期内动车组上线总运行里程。1个预防性维修周期内发生了2次(为随机变量)故障,故其总运行里程为2+1次上线运行里程之和。
约束条件4) 表示不能超期检修。由于中国铁路总公司规定了动车组各项目的预防性检修周期,故可以根据实际情况适当缩短检修周期,但不能进行超期检修。
约束条件5) 表示1个预防性维修周期内发生2次故障,进行2次故障处理所折算的累积运行里程。
约束条件6) 表示预防性维修作业时间太短时检修作业质量不能得到保证,时间太长将影响其他检修项目作业。为保证预防性维修的作业质量,同时考虑作业效率,预防性维修的作业时间需介于上、下限之间,相应地,预防性维修时间折算的运行里程也需介于上、下限之间。
约束条件7) 为惩罚函数,即在1个预防性维修周期内,运行途中所发生故障对动车组可用性的总影响。一方面,动车组入库进行故障处理和周期预防性检修会直接影响动车组的可用性;另一方面,动车组故障常在运行途中发生,当故障发生后,动车组需降速、停车甚至救援,均会影响动车组的可用性。考虑1个预防性维修周期内故障发生的次数和时机,故障次数越多,影响越大;同时,由于故障在运行途中无法修复,运行途中发生故障的时机不同,对运用的影响也不同,故障发生时刻越靠近始发或终到站,对行车影响越小,相反则越大,且这种影响与故障处理时间成正比关系。所以,1个周期内总影响表达为故障发生时,距始发或终到站的距离与进行此故障处理折算的运行里程乘积的累积和。
1.2 Monte-Carlo统计模拟算法
兰新高铁长1 776 km,经历多个大风区,自开通运营以来,一些对风沙敏感的系统、部件和部位因强风沙而发生故障,采用长期统计分析大量此类故障发生的季节、天气、运行里程等,确定出1个具体的维修周期更符合实际,但这需要长时间的动车组运行故障数据积累。本文利用筛选的样本故障信息,推导出目标系统或部件的故障分布函数,然后采用Monte− Carlo模拟仿真的方法来确定维修周期,能准确模拟现实故障发生的随机性,是比较合理、科学的解决方案。
Monte-Carlo统计模拟流程如下:首先收集、筛选因强风沙因素导致的动车组设备故障信息;然后确定系统的故障分布函数,利用筛选的故障数据,对分布函数进行参数估计和假设设检;最后利用确定的故障分布函数,采用Monte-Carlo随机模拟的方法来决策最佳的预防性维修周期。算法流程如图1所示,其中∆为仿真模拟时运行里程增加的步长,其他变量和参数的含义与模型(1)中的相同。算法的思想是逐步增加预防性维修周期,采用Monte-Carlo统计模拟方法,计算每个预防性维修周期下的可用度。为保证计算的稳定性与可靠性,在每个周期下迭代模拟1次,取平均值为该预防性维修周期下的可用度,当达到最高运行里程时结束计算。
2 算例分析
2.1 塞拉门故障数据
自2014年联调联试开始至2017年底,兰新高铁在特殊环境下运行的CRH5型动车组多次在途中发生某车门无法打开或关闭故障,入库检查各控制、机械部件均无异常,原因多为风沙、冰雪进入密封胶条,一段时间后导致胶条上的润滑油脂变质老化、干涩、卡滞、密封不良,通过对密封胶条进行清洁、保养后,车门开闭良好。对此类故障进行整理,故障时对应的运行里程如图2所示。

图1 算法流程
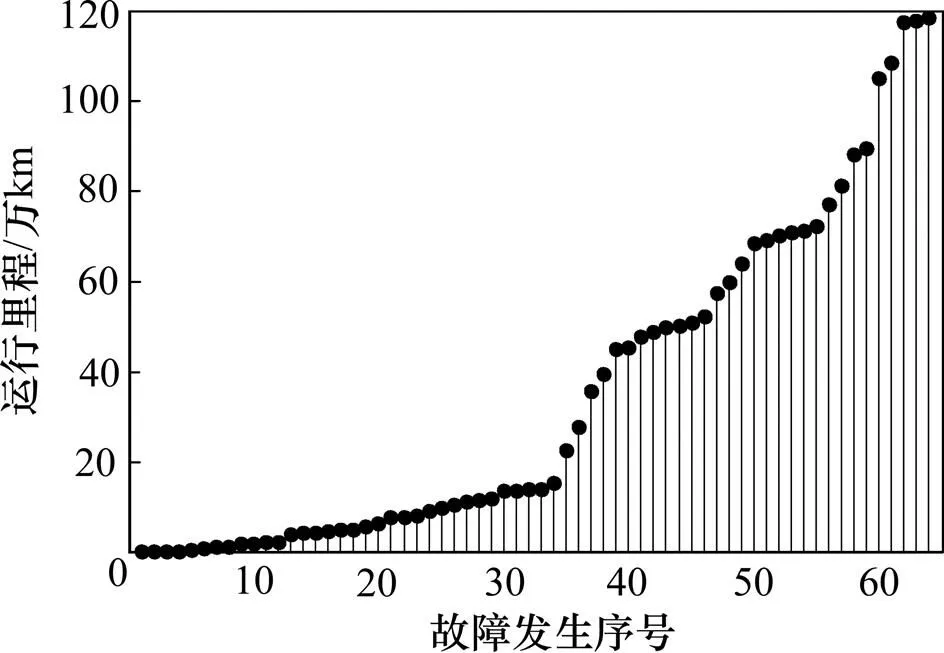
图2 塞拉门故障里程分布
2.2 确定塞拉门故障分布函数
常用的故障分布函数有正态分布、指数分布和威布尔分布。威布尔分布是一种适应面较广的分布形式,在复杂系统的故障率及可靠性研究方面得到广泛应用[13−14]。两参数的威布尔分布函数为:
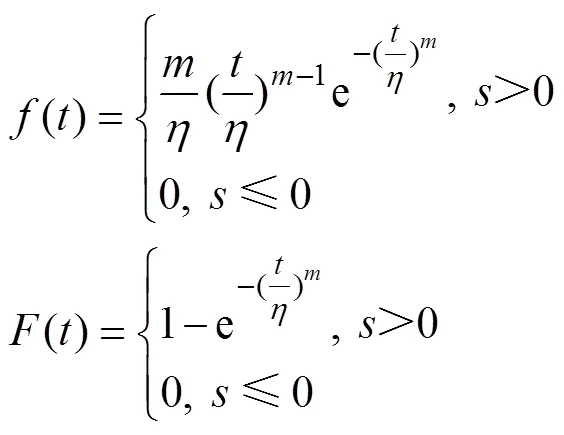
其中:为形状参数;为尺度参数。
参数估计是确定故障分布函数的关键环节,参数估计方法有矩法估计、最小二乘法和极大似然估计等。在各估计方法中,极大似然估计可靠性较好[15−18]。设塞拉门故障服从两参数的威布尔分布函数,利用MATLAB软件,采用极大似然估计法计算各参数值,结果如表1所示。
分布检验是推断故障数据是否服从初步分析所选定的分布类型的一种检验方法。拟合优度是故障数据分布与所选定理论分布之间符合程度的度量,K-S是一种常用的拟合优度检验方法,通过建立统计量D[19]来表征:
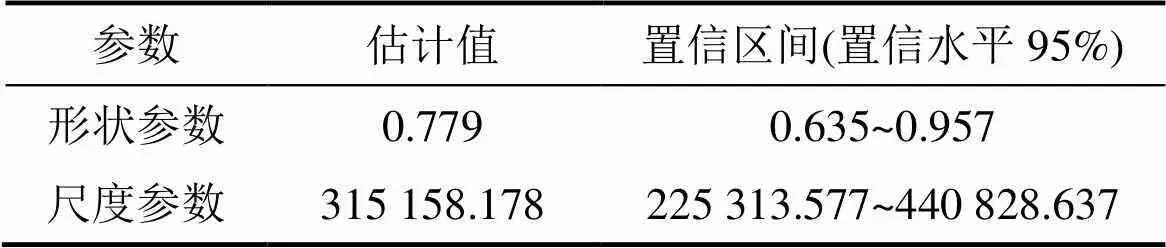
表1 威布尔分布参数估计

其中:0()为计算的分布函数;F()为经验分布函数。当假设问题0:0()=F()成立时,对于给定的可以得到D的精确分布和→∞的极限分布。

1—经验分布函数;2—故障分布函数。
图3 Weibull故障分布函数与经验分布函数对比
Fig. 3 Comparison between Weibull distribution function and empirical distribution function
2.3 塞拉门预防性维修周期计算
通过对班组故障处理和预防性维修作业时间进行统计,其分布分别服从均值为1.72 h和7.53 h、方差为0.12和0.21的正态分布。兰新高铁全长1 776 km,故进行预防性维修的运行里程约为1 770 km的整数倍,故仿真递进步长∆=g=1 770 km;三级(120万km)及以上高级修程,令max=120万km。为保证算法的可靠性与稳定性,每个周期下随机模拟计算2 000次,即1=2 000次;采用不断变化的惩罚等级,即在1个预防性维修周期内,故障越多,惩罚等级越高。
利用各分布函数及上述算法,在MATLAB环境下编程计算,计算结果如图4所示。从图4可以看出:随着预防性维修周期不断增加,动车组可用度先增大,在10万km左右达到最大值,然后随周期增大不断减小。由于CRH5型动车组运用维修修程(一级修除外)为5万,10万,15万和30万km等,最小修程为 5万km,其中塞拉门预防性维修、保养周期为15万km。考虑人员组织及其均衡作业的因素,根据上述仿真计算结果,兰新高铁在强风沙运用环境下,动车组塞拉门的最佳预防性维修周期为10万km。根据现场验证观察,当维修周期为10万km左右时,各塞拉门密封胶条内积尘较明显且存在异物,部分门边胶条上的润滑、密封油脂很少,开始变得干涩,必须进行清洁和保养。

图4 可用度与周期的关系
3 结论
1) 兰新高铁开通后,面临大风、长交路及强风沙的运用环境,与国内其他地区的运用环境存在很大差异。对于运用维修部门而言,预防性维修周期是所面临的主要问题之一。考虑到强风沙环境因素对部分系统的预防性维修周期有很大影响,针对长运行路径及运行途中故障发生时机对动车组有不同影响的特点,建立了基于可用度的预防性维修周期决策模型。
2) 针对兰新高铁开行时间短、运用维修数据少和检修经验不足等问题,提出了利用故障分布函数的Monte−Carlo统计模拟算法。该算法简洁、易实现,实用性强。
3) 对积累的塞拉门故障数据进行筛选、整理,通过故障分布函数类型的假设、参数估计和假设检验,确定了受风沙影响的塞拉门故障服从形状参数为0.779、尺度参数为315 158.178的两参数威布尔分布。利用建立的周期决策模型、算法和故障分布函数,在MATLAB平台下计算了塞拉门预防性维修周期,结合人员组织与均衡作业的因素,得出兰新高铁强风沙环境下CRH5G型动车组的塞拉门预防性维修保养周期为10万km。
4) 由于兰新高铁开行时间较短,受人员素质及技术手段的限制,对风沙敏感的系统、部件如滤网、设备舱等的风沙数据积累还很少,确定这些系统、部件、检修项目的预防性维修周期还需进一步研究。
[1] 康卫林. 高速动车组设备舱通风格栅气粒分离特性的数值模拟[D]. 兰州: 兰州交通大学机电工程学院, 2015: 10−23.KANG Weilin. Numerical simulation of gas-solid separation characteristics on ventilate equipment cabin grille of high-speed train[D]. Lanzhou: Lanzhou Jiaotong University. School of Mechanical Engineering, 2015: 10−23.
[2] 吕立波, 高崎, 李有为, 等. 基于蒙特卡洛仿真的设备维修周期建模与优化[J]. 计算机与数字工程, 2011, 39(4): 47−49. LÜ Libo, GAO Qi, LI Youwei, et al. Maintenance modeling and optimization of equipment based on Monte Carlo simulation[J]. Computer & Digital Engineering, 2011, 39(4): 47−49.
[3] 葛阳, 高崎, 黄照协. 基于可用度的复杂设备维修周期决策模型[J]. 数学的实践与认识, 2012, 42(8): 174−179. GE Yang, GAO Qi, HUANG Zhaoxie. Maintenance interval period decision-making model of complex equipment based on availability[J]. Mathematics in Practice and Theory, 2012, 42(8): 174−179.
[4] MELCHOR-HERNÁNDEZ C L, RIVAS-DÁVALOS F, MAXIMOV S, et al. A model for optimizing maintenance policy for power equipment[J]. International Journal of Electrical Power & Energy Systems, 2015, 68(68): 304−312.
[5] WU Changjie, LI Yanting, XI Lifeng. A preventive maintenance model for leased equipment subject to internal degradation and external shock damage[J]. Reliability Engineering & System Safety, 2016, 154: 1−7.
[6] VILARINHO S, LOPES I, OLIVEIR J A A. Preventive maintenance decisions through maintenance optimization models[J]. Procedia Manufacturing, 2017, 11: 1170−1177.
[7] 丁阳喜, 唐玉杰, 朱韶光, 等. 动车组旋修周期验证研究[J]. 铁道机车车辆, 2015, 35(4): 25−30. DING Yangxi, TANG Yujie, ZHU Shaoguang, et al. Research on the verification of reprofiling cycle for EMU[J]. Railway Locomotive & Car, 2015, 35(4): 25−30.
[8] 赵泽平, 姚建伟, 张可新. 基于可靠性理论制定动车组子系统最佳预防维修周期的方法研究[J]. 铁道机车车辆, 2014, 34(4): 85−89. ZHAO Zeping, YAO Jianwei, ZHANG Kexin. Study of method to calculate the best preventive maintenance period for EMUs subsystem based on reliability theory[J]. Railway Locomotive & Car, 2014, 34(4): 85−89.
[9] 赵金方. 动车组零部件预防性维修周期决策模型的研究[D]. 北京: 北京交通大学机械与电子控制工程学院, 2010: 35−41. ZHAO Jinfang. The study of EMU components preventive maintenance period decision model[D]. Beijing: Beijing Jiaotong University. School of Mechanical, Electronic and Control Engineering, 2010: 35−41.
[10] 孙超. 基于可靠性分析的轨道交通车辆转向架维修周期研究[D]. 南京: 南京理工大学自动化学院, 2014: 37−55. SUN Chao. Research on maintenance cycle of rail vehicle bogie based on reliability analysis[D]. Nanjing: Nanjing University of Science and Technology. School of Automation, 2014: 37−55.
[11] 王彩霞. 高速动车组主要零部件损伤规律及维修周期的研究[D]. 北京: 北京交通大学机械与电子控制工程学院, 2012: 56−62. WANG Caixia. The damage rules and the maintenance cycle of the main components of the high-speed EMU[D]. Beijing: Beijing Jiaotong University. School of Mechanical, Electronic and Control Engineering, 2012: 56−62.
[12] CHARLES E E. 可靠性与维修性工程概论[M]. 康锐, 译. 北京: 清华大学出版社, 2010. CHARLES E E. An introduction to reliability and maintainability engineering[M]. KANG Rui, trans. Beijing: Tsinghua University Press, 2010.
[13] BISTOUNI F, JAHANSHAHI M. Evaluating failure rate of fault-tolerant multistage interconnection networks using Weibull life distribution[J]. Reliability Engineering and System Safety, 2015, 144: 128−146.
[14] GUILANI P P, AZIMI P, NIAKI S T A, et al. Redundancy allocation problem of a system with increasing failure rates of components based on Weibull distribution: a simulation-based optimization approach[J]. Reliability Engineering and System Safety, 2016, 152(C): 187−196.
[15] 金良琼. 两参数Weibull分布的参数估计[D]. 昆明: 云南大学数学与统计学院, 2010: 21−24. JIN Liangqiong. Two parameter estimation for Weibull distribution[D]. Kunming: Yunnan University. School of Mathematics and Statistics, 2010: 21−24.
[16] COORAY K. A study of moments and likelihood estimators of the odd Weibull distribution[J]. Statistical Methodology, 2015, 26: 72−83.
[17] JIAN Xiang, WANG Dong, JIANG Ping, et al. Inference on the reliability of Weibull distribution with multiply Type-I censored data[J]. Reliability Engineering and System Safety, 2016, 150: 171−181.
[18] AYDOĞDU H, ŞENOĞLU B, MAHMUTKARA. Parameter estimation in geometric process with Weibull distribution[J]. Applied Mathematics and Computation, 2010, 217(6): 2657−2665.
[19] 王灵芝. 以可靠性为中心的高速列车设备维修决策支持系统研究[D]. 北京: 北京交通大学机械与电子控制工程学院, 2011: 41−43. WANG Lingzhi. Research on reliability-centered maintenance decision and support system for high-speed train equipments[D]. Beijing: Beijing Jiaotong University. School of Mechanical, Electronic and Control Engineering, 2011: 41−43.
(编辑 陈灿华)
Study on preventive maintenance cycle of sliding plug door of high-speed train in strong blown-sand area
LI Ying1, 2, QI Feng3, YIN Pengfei3, GE Shengchang3, LU Zhaijun1, 4, 5, 6
(1. School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China;2. China Railway Beijing Group Co. Ltd., Beijing 100860, China;3.China Railway Urumuqi Group Co. Ltd., Urumuqi 830011, China;4. Key Laboratory of Traffic Safety on Track (Central South University),Ministry of Education, Changsha 410075, China;5. Joint International Research Laboratory of Key Technology for Rail Traffic Safety, Changsha 410075, China;6. National & Local Joint Engineering Research Center of Safety Technology for Rail Vehicle, Changsha 410075, China;)
To investigate the blown sand environment influence on train-set fault occurrence under long routing operation, a preventive maintenance period decision model based on system availability was proposed. With inadequate running time and maintenance experience on Lanzhou—Xinjiang high-speed railway line, Monte−Carlo-based algorithm was presented for statistical simulation. Real service fault occurrence information of sliding plug door was employed for distribution function definition, parameter estimation and hypothesis testing. Finally, preventive maintenance period of sliding plug door was calculated with MATLAB programming using the suggested model, which was then validated by field test. The results indicate that the fault occurrence of sliding plug door submits to two-parameter Weibull distribution, where the shape parameter is 0.779 and scale parameter is 315 158.178. With the increase of preventive maintenance period, the availability of sliding plug door increases at first and then decreases. Taking factors such as personnel organization of preventive maintenance, balanced operation and repair interval into account, the maintenance period of sliding plug door is determined to be 100 000 km.
strong blown-sand; maintenance cycle; train-set; sliding plug door; Lanzhou—Xinjiang railway for passenger traffic
10.11817/j.issn.1672-7207.2018.09.030
U279.3
A
1672−7207(2018)09−2344−06
2017−11−12;
2018−01−22
国家重点研发计划项目(2016YFB1200104)(Project(2016YFB1200104) supported by the National Key R&D Program of China)
李荧,高级工程师,从事风区铁路行车安全研究;E-mail:liying8806@163.com

