高速钻骨过程中切削力的仿真与实验研究

张立斌，王宇，赵宏强，赵世佳，胡颖

高速钻骨过程中切削力的仿真与实验研究

张立斌1, 2，王宇2, 3，赵宏强1，赵世佳2，胡颖2

(1. 中南大学 机电工程学院，湖南 长沙，410083；2. 中国科学院 深圳先进技术研究院，广东 深圳，518055；3. 哈尔滨工业大学(深圳) 机电工程与自动化学院，广东 深圳，518055)

基于弹塑性有限元模型，实现高速钻骨时骨组织−器械交互状态的仿真；根据动物标本钻骨实验结果，通过优化方法实现模型损伤参数的快速辨识；结合有限元仿真和标本骨实验，研究高速钻骨过程中切削力随不同钻削参数的变化规律。研究结果表明：钻削轴向力仿真结果与实验结果较吻合，验证了损伤参数的有效性及有限元模型的适用性；手术中应该选择较小的进给量和更高的钻速以实现安全钻削。

有限元方法；高速钻骨；损伤参数；优化方法

在骨科手术中，一些骨科疾病如骨折经常会用钢钉等植入体固定骨头，钉道的质量会影响植入体的固定效果及术后恢复，因此钻钉道是关键的手术流程。在钻钉道过程中产生的过大钻削力可能会对骨周围组织造成一定损伤甚至引起裂纹[1]。为了优化钻削效果，有必要对钻骨过程中的钻头与骨组织的交互作用进行研究。作为实验方法的重要补充，计算模型特别是有限元模型已被广泛应用于组织−器械交互的研究[2−6]。LUGHMANI等[1]建立了一个精确的有限元模型研究了低速条件下改变钻削参数而引起的钻削皮质骨的轴向力和扭矩变化规律。SEZEK等[7]基于有限元方法研究了不同的转速、进给量、钻头尺寸等参数和不同性别的骨在钻削过程中所发生的温度变化和热坏死现象。ALAM等[8−9]基于有限元探究了在平面切削皮质骨时切削深度、切削速度等参数对切削力和切削温度的影响。JIN等[10]基于力信号提出了在钻削过程中骨科手术机器人系统状态感知的方法。张青云[11]通过有限元法和实验进行钻削皮质骨性能的研究。国内一些研究人员基于实验分析了在不同钻削参数下皮质骨钻削温度和钻削力的变化规律，如宋金榜等[12]研究了高速微细骨钻过程中的切削力和切削温度的变化规律。上述基于有限元模型模拟钻骨过程的研究中，采用的钻削转速与实际临床医用钻速相差过大，不具临床参考价值。钻削仿真中涉及材料的损伤，而其中损伤演化的位移参数设置尤为重要。本文作者基于优化方法，通过实验数据验证，实现有限元在模拟高速钻骨时模型的关键参数——损伤演化的等效塑性位移的快速辨识，进而完善皮质骨钻削的有限元模型，用于高速钻削过程研究；通过钻骨实验验证损伤参数的有效性，其中钻削转速设置为8 000~23 000 r/min，接近临床中医用骨钻的转速。

1 有限元模型

1.1 几何模型

本文采用标准医疗钻头，其结构参数如下：直径为2.5 mm，顶角为118°，螺旋角为25°，长度为2.5 mm。首先，用SolidWorks软件绘制钻头三维几何模型，然后导入ABAQUS中，进行材料属性赋予、网格划分以及边界条件加载等操作。

研究使用微细的标准医疗钻头，在钻骨过程中钻头对骨头的作用区域仅是很小的一部分，因此，在皮质骨的建模中将骨组织简化为圆柱体，直径为6 mm，高为2 mm。

1.2 材料属性

1.2.1 骨组织力学特性

骨组织的力学行为在弹性范围内遵循Hill的各向异性材料潜在理论和与速率相关的弹性准则[1]。由于皮质骨在力学上具有较低的各向异性相关性，为了便于分析，本文把皮质骨定义为各向同性的弹塑性材料。钻头与皮质骨材料属性如表1所示[1, 13]。

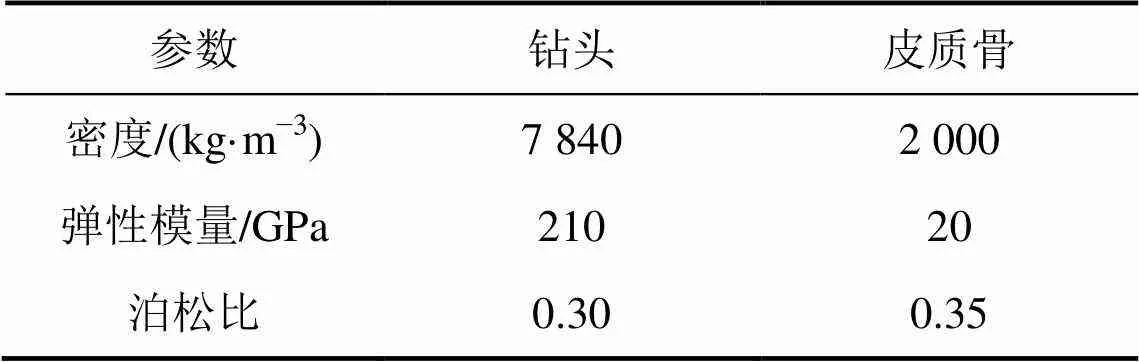
表1 材料参数[1, 13]

1.2.2 骨组织本构模型

在钻削加工中，力的变化是一个非线性过程，材料处在高温、大应变和大应变率情况下。Johnson-Cook模型很适合描述这种依赖应变−应变率的材料属 性[14]。Johnson-Cook材料模型本构方程如下：

表2 Johnson-Cook模型参数

1.2.3 材料失效准则

1.3 网格划分

钻头部分采用自由网格划分技术，划分四面体单元，单元类型为C3D4。骨模型采用细分网格技术，这对模拟大变形和非线性材料行为有很重要的意义。首先分割模型，在钻孔附近细化网格，其他部位使用粗网格，这样划分更加科学有效还可以提高计算效率，节省计算资源。减缩积分单元能更好地模拟网格扭曲十分严重的问题，因此，骨模型单元类型为C3D8R。减缩积分单元容易变形扭曲，产生零能模式，这里使用增强型沙漏控制。本文骨组织有限元模型共80 124个单元，钻头模型共33 615个单元，网格模型如图1所示。

图1 网格模型

1.4 边界条件和接触

在有限元仿真中，皮质骨模型侧面被固定，以限制6个自由度。钻头被约束为刚体，同时设置参考点，并对参考点施加转速和进给量以控制钻头的运动。

接触使用通用接触运算法则，该法则产生的接触力基于罚摩擦公式。钻头和皮质骨接触时的摩擦模型用库仑摩擦来描述，该模型用摩擦因数来表征2个表面之间的摩擦行为，摩擦因数为0.3[15]。

2 钻骨实验

2.1 实验方法

为了验证模型的有效性，探究高速钻骨时轴向力的变化规律，进行不同钻削参数下的钻骨实验。钻骨实验在三轴直线机器人上进行，实验装置如图2所示。骨钻的动力由Maxon电机提供，钻头通过骨钻带动。实验材料选用新鲜的猪肩胛骨，钻头为直径2.5 mm的标准医疗不锈钢钻，使用ATI(Nano43)力传感器采集数据，传感器通过采集卡连接电脑。

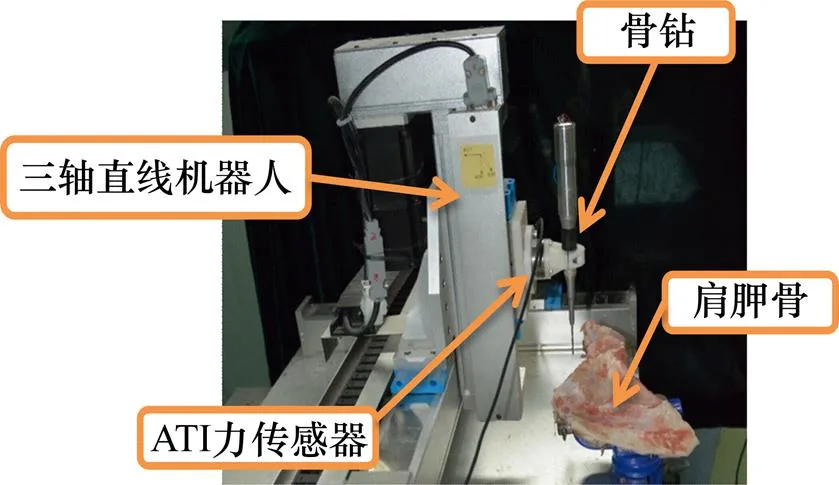
图2 钻骨实验装置

实验开始时，钻头和骨皮质处于接触状态，待钻头转速达到平稳状态，三轴直线机器人带动骨钻以预先设置的进给量穿透皮质骨，同时，ATI力传感器实时记录并保存钻削轴向力数据。

钻骨实验中采用的钻削参数如表3所示。钻头与皮质骨接触时的力有一定波动，取峰值时的力在MATLAB软件中进行均值方差计算，将其计算结果作为实验结果。在有限元仿真中，计算后的力波动较大，使用MATLAB对数据滤波后取均值。

表3 钻削参数

2.2 实验结果

根据上述方法进行实验，实验结果分别如表4和表5所示。

表4 不同进给量下的轴向力(N=8 000 r/min)

表5 不同转速下的轴向力(f=1 mm/s)

3 损伤演化参数辨识

3.1 梯度下降法

梯度下降法是一种最早也最简单的优化方法，其迭代方式简单，易于理解，因此，本文采用梯度下降法对损伤参数进行优化。梯度下降法是沿负梯度方向搜索，求解表达式最小值(或沿上升方向搜索求最大值)的一种方法，过程中越接近目标值，步长越小。

钻削时材料在损伤演化阶段，函数关系如下[1]：

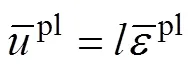
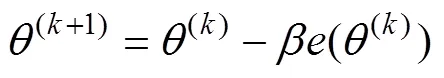
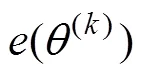
3.2 损伤演化的位移参数辨识

ABAQUS通过损伤演化模拟损伤的发生，损伤演化的类型使用位移模式，在保持模型其他参数不变的情况下，损伤演化的等效塑性位移决定了轴向力，通过调整等效塑性位移参数优化仿真结果。本文参数调节具体流程如图3所示。图3中，为仿真与实验结果的误差，其表达式为

式中：FEA为仿真轴向力；EXP为实验轴向力。

实验时保持转速为8 000 r/min，进给量为 1.5 mm/s，实验得到的轴向力为10.3 N。建立有限元模型，设置初始损伤演化的等效塑性位移参数并计算仿真结果。

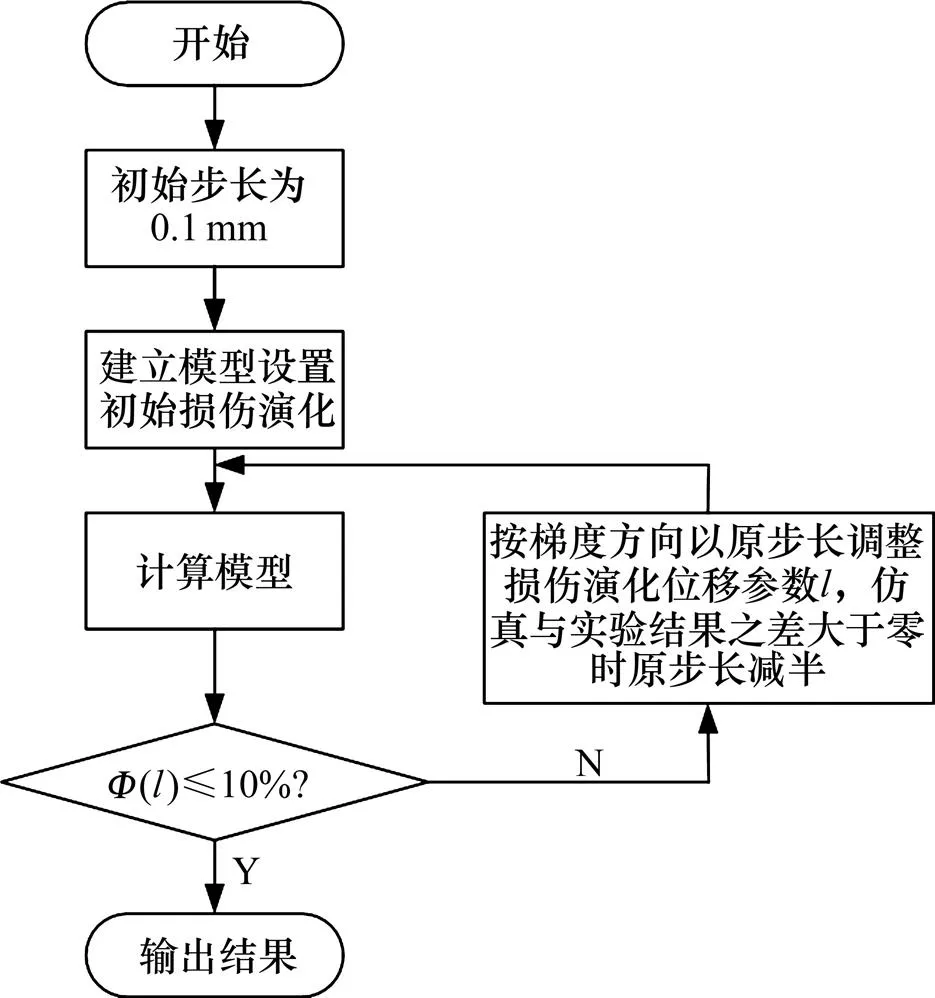
图3 损伤演化调节流程图

将此结果与实验结果进行对比，若相对误差超出10%，则说明此位移参数不合理，然后以一定步长调整此参数，优化仿真结果，最终确定1个合理的位移参数。

仿真实验中等效塑性位移调整了4次，结果如图4所示。保持转速为8 000 r/min，进给量为1.5 mm/s，设置初始位移参数为0.10 mm，初始步长为0.1 mm，仿真得到的轴向力为7.5 N，与实验结果相比误差为27%；随后设置位移参数为0.20 mm，仿真结果仍在误差范围外，相对误差为13%；然后设置位移参数为0.30 mm，计算后相对误差为21%，且仿真与实验结果之差大于0 N，此时步长减半；位移参数取0.25 mm，结果相对误差为2%，在允许的范围内。因此，最终本文等效塑性位移设定为0.25 mm。

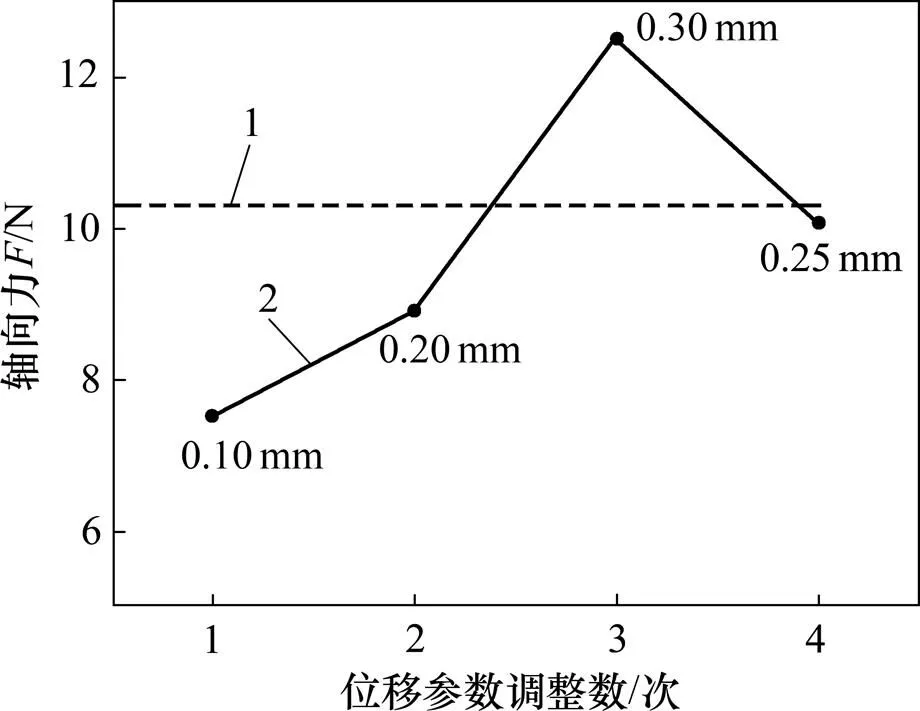
1—实验结果；2—仿真结果。

4 实验验证

4.1 切削应力

钻骨Mises应力云图如图5所示。在仿真研究中材料分离时的最大应力约为150 MPa，这与文献[6]中切削骨仿真和拉伸实验断裂时的应力基本一致。

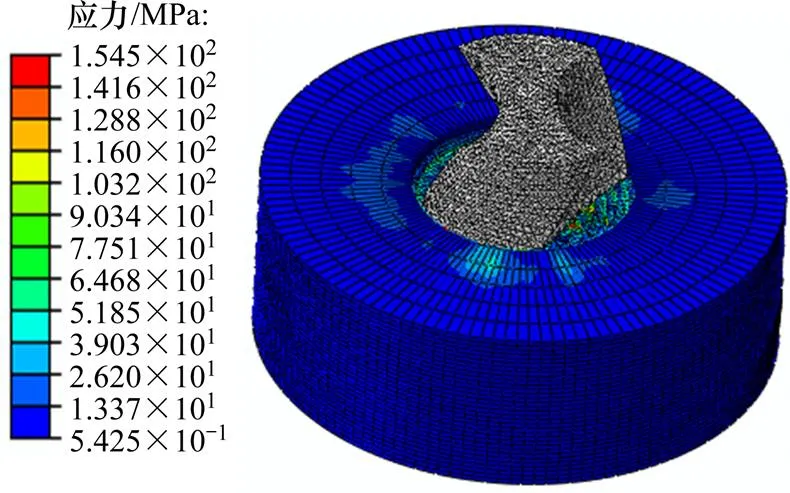
图5 钻骨Mises应力云图

4.2 不同钻削参数下轴向力变化

保持等效塑性位移为0.25 mm不变，改变进给量和钻速，计算仿真结果并与实验结果对比，结果分别如图6和图7所示。

从图6可以看出：保持钻速为8 000 r/min不变，随着进给量增加，轴向力也逐渐增大；当进给量从 1.0 mm/s增加到2.0 mm/s时，轴向力在8~15 N范围内波动。实验轴向力从最低到最高增加了7.12 N，仿真轴向力增加了6.64 N，尤其是在实验过程中，轴向力几乎呈线性增长。保持进给量为1.0 mm/s不变，钻速从8 000 r/min起每次增加5 000 r/min，直至 23 000 r/min(见图7)，随着钻速增加，轴向力减小 2.13 N。因此，在手术过程中，在其他条件不变的情况下，应尽量减小进给量，增加钻速，从而产生更小的切削力。

由图6和图7可知：改变进给量时轴向力变化幅度为6~7 N，波动较大，而改变钻速时轴向力变化幅度小于3 N，波动相对较小。通过对比可知进给量对轴向力的影响比钻速的影响大，这也符合钻削轴向力经验公式所体现的规律。

1—实验结果；2—仿真结果。

1—实验结果；2—仿真结果。

本文作者使用相关系数对数据进行量化，相关系数表达式为

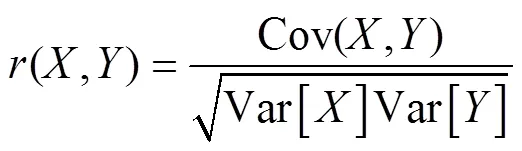
式中：和为变量；Cov(,)为和的协方差，Var[]和Var[]分别为和的方差。通过求解可得图6和图7中2组数据相关系数分别为1=0.997 2，2=0.982 0。从2个相关系数可以得到在改变进给量和钻速时，仿真所得到的钻削轴向力结果与实验结果有很高的吻合度。这证明了本文作者所提的基于优化方法，通过实验验证，实现位移参数快速辨识方法的正确性，同时也证明了仿真所设置的等效塑性位移参数设置是合理、有效的，表明本文作者建立的有限元模型适用于模拟高速钻骨过程。

5 结论

1)建立了1个弹塑性有限元模型用来模拟高速钻骨过程，基于优化方法，通过实验验证，实现了有限元在模拟高速钻骨时模型的关键参数即等效塑性位移参数的快速辨识。

2)在手术中，为了避免过大的切削力对骨周围组织的损伤，应该选择较小的进给量和更高的钻速；在临床手术中，为了不产生过大的切削力，进给量应小于1.0 mm/s，转速应高于23 000 r/min。

[1] LUGHMANI W A, BOUAZZA-MAROUF K, ASHCROFT I. Drilling in cortical bone: a finite element model and experimental investigations[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2015, 42(8): 32−42.

[2] ZHAO Shijia, GU Linxia, FROEMMING S R. On the importance of modeling stent procedure for predicting arterial mechanics[J]. Journal of Biomechanical Engineering, 2012, 134(12): 121005-1−121005-6.

[3] 聂涌, 马俊, 胡钦胜, 等. 髋臼假体放置角度对髋臼周围应力分布的影响[J]. 医用生物力学, 2014, 29(4): 1−7..NIE Yong, MA Jun, HU Qinsheng, et al. Influence from acetabular component orientation on stress distribution of periacetabulum[J]. Journal of Medical Biomechanics, 2014, 29(4): 1−7.

[4] Karaca F, Aksakal B, Kom M. Influence of orthopaedic drilling parameters on temperature and histopathology of bovine tibia: an in vitro study[J]. Medical Engineering and Physics, 2011, 33(10): 1221−1227.

[5] Wang Yu, Cao Meng, Zhao Xiangrui, et al. Experimental investigations and finite element simulation of cutting heat in vibrational and conventional drilling of cortical bone[J]. Medical Engineering and Physics, 2014, 36(11): 1408−1415.

[6] Qi Lin, Wang Xiaona, Meng M Q. 3D finite element modeling and analysis of dynamic force in bone drilling for orthopedic surgery[J]. International Journal for Numerical Methods in Biomedical Engineering, 2014, 30(9): 845−856.

[7] SEZEK S, AKSAKAL B, KARACA F. Influence of drill parameters on bone temperature and necrosis: a FEM modelling and in vitro experiments[J]. Computational Materials Science, 2012, 60(5): 13−18.

[8] ALAM K, MITROFANOV A V, SILBERSCHMIDT V V. Finite element analysis of forces of plane cutting of cortical bone[J]. Computational Materials Science, 2009, 46(3): 738−743.

[9] ALAM K, MITROFANOV A V, SILBERSCHMIDT V V. Thermal analysis of orthogonal cutting of cortical bone using finite element simulations[J]. International Journal of Experimental and Computational Biomechanics, 2010, 1(3): 236−251.

[10] JIN Haiyang, HU Ying, DENG Zhen, et al. Model-based state recognition of bone drilling with robotic orthopedic surgery system[C]// The 2014 International Conference on Robotics and Automation (ICRA). Chicago, USA: IEEE,2014: 3538−3543.

[11] 张青云. 基于ABAQUS的皮质骨钻削性能的仿真和试验研究[D]. 天津: 天津理工大学机电工程学院, 2014: 46.ZHANG Qingyun. Finite element analysis and experimental research of cortical bone drilling performation based on ABAQUS[D]. Tianjin: Tianjin University of Technology. School of Mechanical Engineering, 2014: 46.

[12] 宋金榜, 陈明, 赵梓涵, 等. 高速微细骨钻过程中切削力与切削温度试验研究[J]. 机械设计与制造, 2015(4): 137−139. 143. SONG Jinbang, CHEN Ming, ZHAO Zihan, et al. An investigation on cutting force and temperature during high speed micro-drilling on bone[J]. Machinery Design & Manufacture, 2015(4): 137−139, 143.

[13] TU Yuankun, CHEN Liwen, CIOU J S, et al. Finite element simulations of bone temperature rise during bone drilling based on a bone analog[J]. Journal of Medical & Biological Engineering, 2013, 33(3): 269−274.

[14] 刘森. 骨铣削过程中切削力和温度的仿真与实验研究[D]. 哈尔滨: 哈尔滨工业大学机电工程与自动化学院, 2014: 58.LIU Sen. Research on simulation and experimentation of cutting force and temperature for bone milling[D]. Harbin: Harbin Institute of Technolog.School of Mechanical Engineering and Autmation, 2014: 58.

[15] MELLAL A, WISKOTT H W A, BOTSIS J, et al. Stimulating effect of implant loading on surrounding bone[J]. Clinical Oral Implants Research, 2004, 15(2): 239−248.

[16] 陈海波, 吕咸青, 乔彦松. 梯度下降法在沉积物粒度分布拟合中的应用[J]. 数学的实践与认识, 2011, 41(13): 78−87. CHEN Haibo, LÜ Xianqing, QIAO Yansong. Application of gradient descent method to the sedimentary grain-size distribution fitting[J]. Mathematics in Practice and Theory, 2011, 41(13): 78−87.

(编辑 伍锦花)

Computational simulation and experimental research on cutting force during high-speed bone drilling

ZHANG Libin1, 2, WANG Yu2, 3, ZHAO Hongqiang1, ZHAO Shijia2, HU Ying2

(1. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;2. Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China;3. School of Mechanical Engineering and Automation, Harbin Institute of Technology, Shenzhen 518055, China)

A finite element model was constructed to simulate the interaction between bone tissue and device during high-speed bone drilling. Based on the result fromdrilling experiment and the optimization method, the damage parameter used in the finite element model was identified. Combining the finite element simulation and theexperiment, variations of cutting force along with the changes in drilling parameters during the process of high-speed bone drilling were studied. The results show that simulation result of drilling axial force coincides with that ofexperiment, which validates the effectiveness of damage parameter and the applicability of finite element model; lower feeding rate and higher drilling speed should be adopted to ensure drilling safety in orthopedic surgery.

finite element method; high-speed bone drilling; damage parameter; optimization method

10.11817/j.issn.1672-7207.2018.09.011

TH781

A

1672−7207(2018)09−2191−06

2017−10−31；

2017−12−19

国家自然科学基金资助项目(61573336)；深圳市基础研究重点项目(JCYJ20160608153218487) (Project(61573336, U1613224) supported by National Natural Science Foundation of China; Project(JCYJ20160608153218487) supported by Key Fundamental Research Program of Shenzhen)

胡颖，博士，研究员，从事医疗机器人研究；E-mail: ying.hu@siat.ac.cn