光电复合海缆导体温度计算及参数修正

潘梦琦，唐永卫，陈元林，卢学佳

（1.上海海事大学信息工程学院，上海 201306；2.国网衡水供电公司，衡水 053000；3.江苏海上龙源风力发电有限公司，南通226408）

0 引言

导体温度是决定海缆寿命的重要因素[1]，也是确定载流量的重要依据[2]，因此需要准确计算导体温度。

目前对单芯电缆进行导体温度计算的研究案例较多[3,4]，但对于三芯电缆，其径向结构不对称，使用热路法计算导体温度困难，中文期刊中仅有少量与三芯电缆导体温度计算相关的文献。文献[5]建立了三芯电缆的暂态热路模型，运用IEC 60287计算模型参数。文献[6-8]建立了三芯电缆稳态热路模型，研究电缆表面温度与导体温度的关系。IEC 60853标准建立暂态热路模型时同时考虑了热阻和热容两种参数；计算多阶跃下的导体温度时，它指出需考虑损耗随电流变化的情况。文献[5-8]相较于IEC 60853标准，在计算变负荷下导体温度的过程中均未加入热容参数，且没有考虑损耗随电流变化的情况。另外，电缆内各层结构的热阻会随导体温度发生变化，IEC 60853标准在计算时忽略了这一点。

本文考虑以上文献存在的不足，找到了一种更为可靠的方法。以某海上风电场220kV三芯光电复合海缆为例，对各层结构热阻进行灵敏度分析，找到对计算结果影响最大的热阻参数；通过布里渊光纤时域分析仪（BOTDA）实测得到光纤温度变化量，根据有限元建模分析光纤与导体温度变化量的对应关系；最后利用导体温度变化量修正热阻参数，从而提高计算结果的准确性。

1 IEC 60853计算导体暂态温升方法简介

IEC 60853标准是IEC（国际电工委员会）制定的用于计算电缆周期性负载和紧急负载的通用准则。其中IEC 60853-2针对110kV以上高压电缆提出一种基于热路法的导体暂态温升计算方法。

针对三芯电缆计算导体暂态温升，IEC 60853标准首先在总导体损耗不变的情况下将其等效成单芯结构；之后采用热回路-电回路类比模式，将热阻比拟于电阻、热容比拟于电容、热流量等效于电流、温差等效于电压来构造电缆暂态热路模型；为了能够描述完整的绝缘储热性能，该标准利用Van Wormer[9]因子分配导体和护层间的绝缘热容，通过合并热阻、热容将复杂的暂态热路模型简化为双口网络结构；最后根据电流持续时长将暂态温升计算公式分为三种情况。

本文将基于热路法的导体暂态温升计算过程分为三芯海缆结构确定、单芯结构等效、热路模型建立与简化和导体暂态温升计算4个步骤。导体温度计算流程如图1所示。

图1 导体温度计算流程

2 热阻灵敏度分析

IEC 60853标准在计算实时导体温度时假设热阻不变，但实际上热阻会随导体温度的变化而改变，因此若不考虑绝缘层热阻的变化情况会影响计算结果的准确性。由于电缆结构层热阻参数较多，需要对热阻进行灵敏度分析。

设θ为由热路模型法计算得到的导体暂态温升，假设结构层i的热阻Ti变化百分比为P，θi为结构层i热阻参数变化后得到的导体暂态温升，定义结构层i的热阻灵敏度为Si[10]。

结合本文第3节中实际海缆参数，根据IEC 60287标准计算得到稳态下的绝缘层热阻T1、填充层和内垫层热阻之和Tf以及外被层热阻T3分别为0.589、0.056和0.037。对海缆施加负载电流300A，稳定后的导体暂态温升为6.52℃。将三个热阻参数分别增加50%，重新计算导体暂态温升，进一步得到热阻灵敏度Si，热阻灵敏度对比如表1所示。

表1 热阻灵敏度对比

由表1可知：绝缘层热阻变化对计算结果影响最大，故需要对该参数进行修正。

3 绝缘层热阻参数修正方法

3.1 修正方法概述

由IEC 60853标准给出的导体暂态温升计算公式θ=f(ΔI,T1,Z)，其中ΔI为电流变化量，T1为绝缘层热阻，Z代表其它未列出的海缆结构、热阻、热容等参量。可见在已知ΔI、θ及Z的条件下，可求得绝缘层热阻T1，从而达到实时修正该参数的目的。

3.2 修正实现的难点分析

实际工况中无法通过测量工具直接获取导体温度，即难以得到导体暂态温升。针对以上问题，本文提出一种有效的方法。通过布里渊光纤时域分析仪（BOTDA）实时获取不同负荷电流下的光纤温度变化量ΔTfb，利用光纤与导体温度变化量的对应关系，推算得到导体温度的变化量ΔTc，将其代入式θ=f(ΔI,T1,Z)中可实时修正绝缘层热阻T1。因此，准确获取光纤与导体温度变化量的对应关系显得尤为重要。

3.3 光纤与导体温度变化量对应关系分析

目前在研究光纤与导体温度关系方面使用较多的是热路模型法和有限元法。热路模型法从理论上证明三芯海缆中导体与光纤温度之间满足固定的线性函数关系，此关系与外界环境温度无关[11]。然而实际工况中的海缆结构和边界条件复杂，利用热路模型法分析光纤与导体温度间的对应关系会造成一定的计算误差。

故本文采用有限元法构建海缆各层结构，分析海缆本体和周围环境温度场，对不同负载电流下的光纤温度和导体温度数据进行分析，从而获得海缆中光纤温度变化量与导体温度变化量的对应关系。

对本文第4节实验中使用的海缆进行有限元分析，土壤与海水表面传热系数为200W/m2∙℃，对海缆施加不同的负荷电流，仿真环境温度在20℃条件下的温度分布，提取光纤温度与导体温度数据，结果见表2。

表2 环境温度20℃时不同负荷下光纤与导体温度数据

用最小二乘法对光纤温度和导体温度进行线性拟合，得到20℃环境温度下导体温度与光纤温度的关系：

式中，Tc是环境温度20℃下的导体温度；Tfb是环境温度20℃下的光纤温度。拟合确定系数0.999、方均根误差0.05℃。可见，导体温度与光纤温度存在线性关系，光纤温度每变化1℃，导体温度相应变化2.89℃。

4 实例验证

本文以某海上风电场采用的型号为HYJQF41-F 127/220 3×500+2×36C220kV的三芯光电复合海缆为计算实例。海缆结构如图2所示：

图2 三芯光电复合海缆截面图

实验中的海缆结构参数、材料参数和环境参数如表3所示。

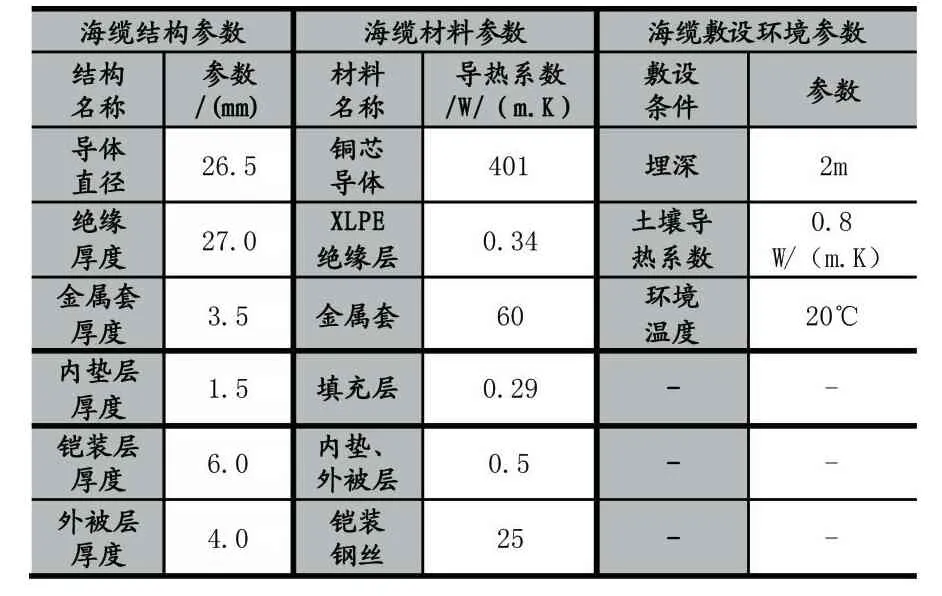
表3 海缆参数表

4.1 负载电流采样

本文利用实际工况中24小时内电流连续上升与下降的情况来分析导体的温度变化。将海缆尚未通入电流时刻作为初始状态，每1小时对负荷电流采样一次，数据记录于表4中。

表4 负荷电流值和持续时间表

4.2 光纤温度采集

本试验利用布里渊光时域分析（BOTDA）设备对光纤温度进行连续测量，每隔一小时记录一次光纤温度数据并计算光纤温度变化量，如表5所示。

表5 光纤温度信息采集表

4.3 实时修正绝缘层热阻

根据文中3.3节得到的导体与光纤温度变化量对应关系，结合表5中光纤温度变化量数据，计算出导体温度的实际变化量ΔTc1。将IEC 60287计算出的稳态绝缘层热阻值0.589作为暂态计算的初始值，并由其生成搜索区间[0，1]，利用穷举法按照间隔为0.001将搜索区间内的数值代入导体暂态温升计算过程得到导体温度的理论变化量ΔTc2。比较ΔTc1与ΔTc2之间的偏差，当偏差小于设定的阈值0.01时，则认为当前代入的数值即为实时绝缘层热阻，修正后的绝缘层热阻值如表6所示。

4.4 导体暂态温升曲线对比

本文根据实时负荷和环境温度分别在考虑绝缘层热阻变化与未考虑绝缘层热阻变化两种情况下推算出导体暂态温升，并将其绘成如图3所示的曲线。图3中，横轴为时间，纵轴为导体暂态温升。蓝色曲线对应未考虑绝缘层热阻变化的导体暂态温升；黑色曲线对应考虑绝缘层热阻变化的导体暂态温升；将由光纤温度变化量推算得到的导体温度变化量作为导体暂态温升的实际值，对应图中的红色曲线。

图3 导体暂态温升曲线对比

导体暂态温升正值表示导体温度升高，负值表示导体温度降低。由图3中三条曲线的正负数值可以看出，导体温度的变化趋势基本一致。类似于向量的相似度，本文将欧氏距离的长短作为评判数据间偏差大小的依据，分别计算蓝色曲线、黑色曲线与红色曲线间的欧氏距离为2.75、1.54，说明黑色曲线与红色曲线间的距离更近，即考虑绝缘层热阻变化的导体暂态温升数据与实际值的偏差更小。

5 结语

本文介绍了IEC 60853标准中基于热路法计算导体暂态温升的方法；利用有限元建模分析光纤与导体温度变化量的对应关系，由此关系实时修正绝缘层热阻，从而提高导体暂态温升计算的准确性。通过与实际数据对比并进行偏差分析，验证了此方法的可行性。根据此方法可以提高110kV以上高压光电复合三芯海缆导体温度计算的准确性，为海缆寿命以及动态载流量的确定提供更有力的依据。

创新点说明：

（1）导体温度计算过程中考虑绝缘层热阻变化对计算结果的影响（首次发表）

（2）利用光纤温度变化量修正绝缘层热阻（首次发表）