基于基因表达调控概率的基因选择方法

储宇强

安徽大学经济学院，合肥，230601

根据中国癌症中心发布的《2017年中国肿瘤登记年报》显示，我国每天约有1万人被确诊癌症，平均每分钟就有7人，其中肺癌的发病率和死亡率高居榜首。此外，癌症种类复杂多样，且具有较长潜伏期和较高复发率[1]，早期癌症的医学诊断和分类成功率不容乐观。因此，积极探索实用有效的方法对癌症进行精确诊断和预测至关重要。

1 研究背景与现状

DNA微阵列(DNA Microarray)，又称基因芯片，可监测细胞基因表达水平，具有高效率、高通量和集约化的特性[2]。从发病机制看，癌症是复杂的基因病，通常由基因突变以及基因表达的改变所导致。因此，基于基因表达谱数据中差异表达信息，能够识别并筛选出癌症关键基因[3]。众所周知，基因表达调控(regulation of gene expression)是指对基因转录和翻译的起止及发生速率的调节过程。转录的进行要有RNA聚合酶来催化，RNA聚合酶对DNA序列的特异性识别须转录因子(transcription factor)介导[4]，转录因子对DNA序列的绑定具有双重作用，通常称能促进基因转录活动的调控为“上调控”，抑制基因转录活动的调控为“下调控”。

截至目前，已有各种不同的方法用于解决基因选择的难题。1999年Golub等人在分析白血病DNA微阵列数据时提出了“信噪比”(signal-to-noise ratio)准则，引领了利用基因表达谱数据解决肿瘤基因筛选难题的方向[5]。随后，研究者提出基于概率模型的基因选择算法，且实验结果更显著有效。Baldic等人提出了进行降维的贝叶斯方法[6]；2005年，李颖新等人提出“分类信息指数”分类标准，使用SVM-RFE 的方法进行基因选择[7]。2006年，李建中等人提出一种与样本类别分布没有联系的基因筛选算法[8]。由于绝大多数的变量信息隐藏在数据中，需要通过概率统计模型推断或集成得出，所以,使用概率统计方法对DNA微阵列数据分析具有必要性。本文基于基因表达调控概率，筛选癌症关键基因，并在肺癌数据集上进行模拟验证，结果表明本文所提出的方法能够高效实现癌症关键基因的选择。

2 建立基因表达调控概率模型

2.1 基因调控概率的定义

外部环境会影响基因的表达水平。通过建立基因表达调控概率模型，可以预测有特定表现型的关联基因或疾病。考虑到二元的情况，假设微阵列数据可以用G行S列的微阵列表达数据矩阵E表示。其中，元素ag1s1指基因g1在样本s1中的表达水平测得值。在矩阵E中行向量代表基因，纵向量代表样本，把所有样本分为两类，分别以Y=1和Y=-1表示。假设Y=1类中的样本数目为m，Y=-1类的为n，每一个目标样本s可以由Ys∈{1,-1}表示，则有m+n=S恒成立。

相对于某种外部环境，基因在差异环境下可能具有三种表达调控状态:非显著调控状态、上调控状态和下调控状态。下文分别给出各调控状态的数学定义及计算公式。

定义1上调控概率。对于一基因g，令

(1)

(2)

pgsu指以Y组类为参考时，基因g在样例s中的上调控概率。(其中，a为基因在参考组样例中的表达值，ags为基因g在样本s中的表达值，q为参考样例数目)

定义2下调控概率。对于一基因g，令

(3)

(4)

pgsd指以Y组类为参考时，基因g在样例s中的下调控概率。(其中，a为基因在参考组样例中的表达值，ags为基因g在样本s中的表达值，q为参考样例数目)

2.2 基因调控概率的计算

从统计的角度，由一个样本推断基因的潜在规则是不够的。因此，本文对每一个基因定义了如下两种调控事件：

定义3调控事件U。基因g在样类Y=1中的表达水平总是高于在样类Y=-1中的表达水平，即U:(ag(y=1)>ag(y=-1)) ，该事件的发生概率被称作上调控事件概率并以符号P(U) 表示。

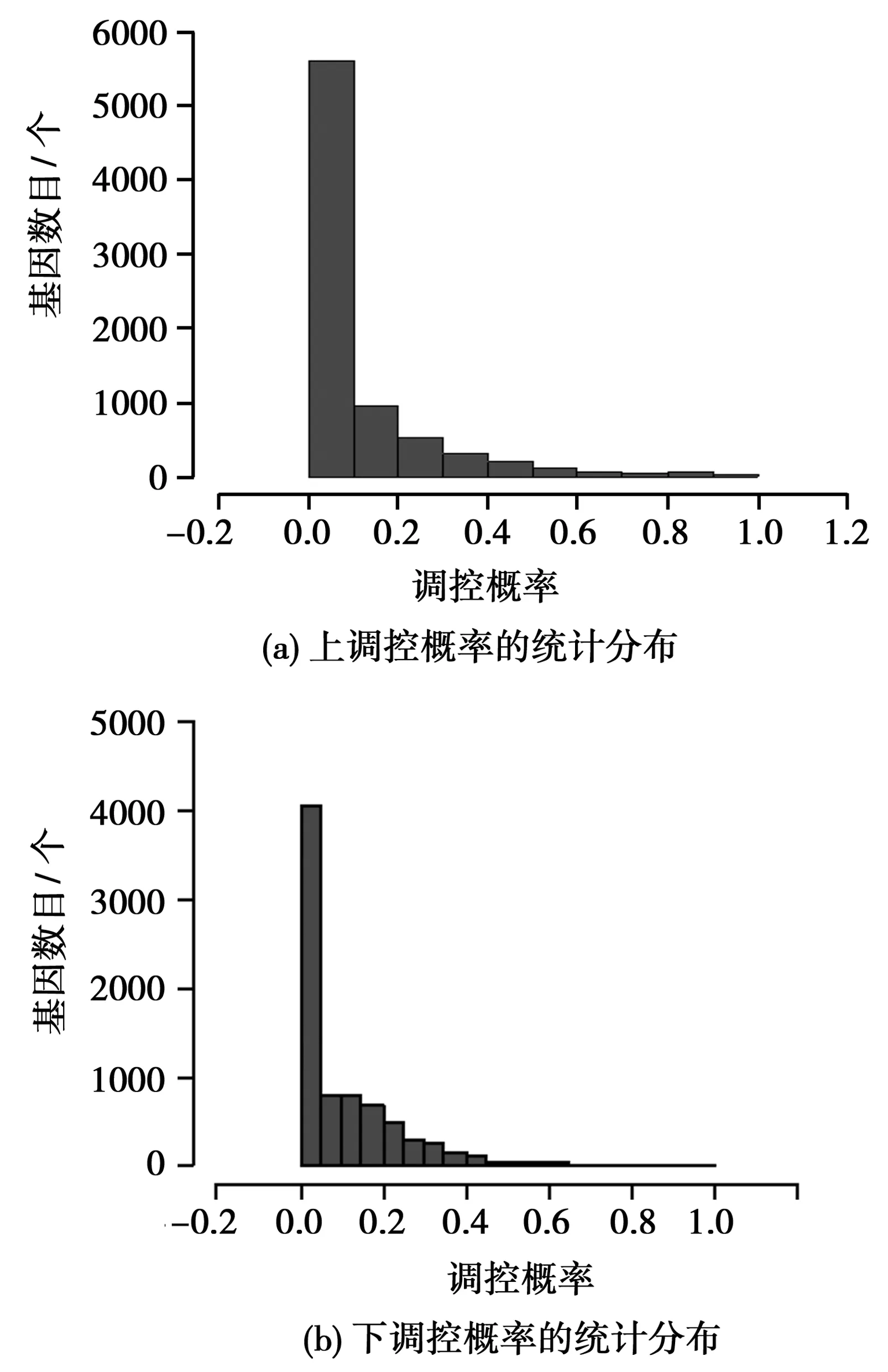
定义4调控事件D。基因g在样类Y=1中的表达水平总是低于在样类Y=-1中的表达水平，即D:(ag(y=1)

因为绝对独立的基因表达调控概率不能得到，本文选择使用在一个特定的背景情况C的条件概率，而不是绝对的独立事件的概率。在实践中，背景条件C的使用，对类的区别有助于提前过滤不相关的基因。

所以，用符号P(U)表示基因在上述一定的背景条件下的上调控事件概率，利用平均信息产生背景条件C，基因表达调控事件概率由统计知识分别给出算法。

上调控事件概率P(U)：

(5)

下调控事件概率P(D)：

(6)

其中，S为总样本数，pdgi为在以{Y=1}类为参考组时，基因g在{Y=-1}类中样例i的下调控概率；pugi为在以{Y=-1}类为参考组时，基因g在{Y=1}类中样例i的上调控概率。

3 基于基因表达调控概率的基因选择

一般来说，微阵列数据往往具有高冗杂性，因此，实验中会有大量多余的不相关基因的存在，这将增加癌症关键基因辨认的复杂程度，不仅使分类算法的精度降低，还加大了计算量[9]。因此，在运行算法之前，有必要对基因表达谱数据进行预过滤处理。

本算法使用平均值产生背景条件C过滤掉两样本类中表达水平差异比较小的基因。之后，剩余基因被收集作为初步基因集，关键基因将使用基因表达调控信息来选择。

背景条件C可以表示为C:|u1-u2|≥θ，u1、u2分别是两样本类的基因表达水平的平均值。θ称为类间表达差异截止阈值，取决于基因在两样本类中表达水平的平均差异的最值，即范围：θmin<θ<θmax

在同一时刻，基因的上、下调控事件互斥。当上调控事件发生时，则P(U)将很大，即P(D)就会很小。此时，若取两个调控概率的绝对差PD，即:

PD=∣P(U)-P(D)∣

(7)

理想情况下该值等于1。但由于微阵列数据的高变异性和高噪声属性，该值将应该接近，但不完全确定地等于1。同理，在两个事件都不发生时，两个调控概率P(U)和P(D)都应该接近于0.5，而此时他们的绝对差值应该近似为零。综上所述，基因在不同的实验条件下所表现出的调控性质，可以用调控概率差的绝对值PD体现。因此，可以用基因表达调控概率的绝对差值来识别和筛选癌症基因。

最后，本算法可以概括如下：

步骤一：初始化阈值因子φ。

步骤二：使用背景条件C，对基因进行预过滤。

步骤三：计算出基因调控概率矩阵。

步骤四：根据步骤三所得矩阵，使用公式(5)和公式(6)计算两种调控事件概率P(U)和P(D)。

步骤五：计算基因表达调控事件概率差的绝对值，并以此作为筛选肿瘤特征基因的依据。

4 在肺癌数据集(Selmat2012)上的应用

采用广泛使用的肺癌数据集Selmat数据[10]验证算法。Selmat数据集由116个样本构成，包含58个正常样本和58个肺癌样本。每个样本含25 441个基因表达数据。

应用本算法，对肺癌数据进行如下符号设定：将未患肺癌子群看作Y=1 类；将肺癌子群看作Y=-1类。这样，由数据集的大小可得出下列变量：m=58，n= 58。然后，根据基因在两子类间表达水平差异的最值初始化阈值因子φ。本实验中，φ值被设置为两子类基因表达水平的平均差异绝对值的最大值的1/20，即：φ=0.239 543 5。最后，依据上述参数设置运行本算法。求出所有满足背景条件C的基因的上调控事件概率P(U)和下调控事件概率P(D)，然后以基因表达调控事件概率差异的绝对值大小为标准筛选基因。结果如下：

图1 基因表达调控概率的统计分布图

图1分别显示了上调控和下调控概率的统计分布直方图。可知，无论是P(U)还是P(D)的分布统计图，极少数基因表达调控概率值接近于1，而绝大多数基因的调控概率值趋近于零点。该分布图也从侧面印证，在Selmat数据所含基因中，只有少量基因与两Selmat子类的差别有关联，绝大部分是无关基因，而其在两个Selmat子类之间的调控概率较高。图2显示了在Selmat数据上两类基因表达调控事件概率的绝对差值PD的概率分布直方图，从图中可以看出，绝大部分的基因的PD接近于零，只有极少数的基因与癌症有关，这也验证了图1的结论。表1给出了本算法依据PD大小筛选出的前20个基因。

图2 两调控事件的差的绝对值(PD)的分布图

PDGenegSYMBOLsgIDs1.00000"DEPDC7""91614"1.00000"CNGB1""1258"1.00000"C9""735"1.00000"C20orf86""140731"1.00000"BRD2""6046"1.00000"ACACB""32"1.00000"ACACA""31"0.982759"ATP6V0A2""23545"0.965517"GGCX""2677"0.965517"FADD""8772"0.965517"ERG""2078"0.965517"ARL1""400"0.956897"FGF10""2255"0.956897"C18orf58""284222"0.956897"C14orf129""51527"0.948276"GALNT12""79695"0.948276"C1orf186""440712"0.939655"FLJ20054""54530"0.939655"DKFZp686E2433""345462"0.939655"CHCHD6""84303"

PD：基因上、下调控事件概率差的绝对值；

gSYMBOLs:基因名字;

gIDs:基因编号。

为了检测结果的准确性，在同一个Selmat数据集上，运用相关的微阵列数据分析方法[11]计算，然后将两种算法所筛选基因的对比结果统计列入表2。从表2 可知，两种算法所选取的前15个关键基因完全相同，前20 个基因也达到了82%的准确度，表明通过调控概率绝对差值选取的关键基因具有较高的准确率。此外，为了更好地评价本算法，将算法的分类结果与基于贝叶斯变量选择的分类方法和部分最小二乘模型方法的分类结果相比较，得出的结果如表3所示。从表3可知，本文所选取的基因选择方法分类正确率为100%，分类结果较为准确，同时所使用的基因数目为22，表明本算法具有较好的分类性能。

统计本算法与文献[11]算法所选不同数目基因的准确度，见表2。

表2 两种算法选择基因的准确度

GN:两种算法选取的基因数目;

交集数：相同基因数目;

并集数：基因种类数目。

表3 基于基因表达调控概率的基因选择方法分类结果与其他文献报道结果的比较

5 总结与展望

DNA微阵列技术的发展及应用使肿瘤疾病的预测及治疗成为可能[12]。但是，基因微阵列数据具有高冗余和高噪声等特性，为有效解决传统选择方法在分析微阵列数据时产生的过拟合或维数灾难的问题，本文基于基因在不同组织样本中的差异表达调控信息，提出了基于基因表达调控概率的基因选择算法[13]。在公开的Selmat数据上的实验表明，本算法所选取的癌症关键基因的正确率达到了90%以上。此外，在同一数据集上运用其他文献的方法来检验本算法的结果，也显示本算法筛选关键基因的准确性更高。

综上所述，采用本文提出的基于基因表达调控概率的基因选择算法可以提取关键基因，而且避免了调控状态系数选取对基因筛选的影响。本文尚未研究基因序列的改变对筛算结果产生的影响，因此，可以尝试改变基因序列来进一步研究关键基因的提取结果。