正方体中几种常见的截面作法

□ 海南师范大学附属中学 廖云霞

如果用一个平面去截几何体，那么该平面与这个几何体的各个面相交，由交线围成的平面图形叫几何体的截面。打个比方，木匠用锯子将某个小木块锯成两块，“锯口”就是我们所说的截面。本文将以正方体为载体，展开讨论关于截面的如下两个问题：一是过三点（均在棱上）作正方体的截面的做法；二是截面面积或周长的计算。通过研究正方体的截面问题，我们能更好地揭示空间图形与平面图形之间的内在联系。

因为正方体的各个面都是平面，所以用平面去截它所得的截面必是多边形。由于截面至少与正方体的三个面相交，至多与六个面相交，所以截面的形状只能是三角形、四边形、五边形、六边形四种。截面与正方体每一个面的交线由两个公共点决定，所以只要找到截面与正方体某个面的两个公共点，就能做出截面与该面的交线。公共点与交线的求得，主要依据为：

1.公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内。

2.公理2:过不在一条直线上的三点，有且只有一个平面，及公理2的三个推论。

3.公理3:如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

4.面面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

5.如果三个平面两两相交，那么所得三条交线平行或共点。

例1.已知正方体ABCD-A1B1C1D1的棱长为1，E是棱AB的中点，F是棱CC1的中点。做过D1、E、F三点的截面，并求截面图形的周长。

图1

作法1（延长线法）：如图1，分别延长D1F、DC交于点 P；连接 PE，交 BC于点 N；延长 PE，交 DA的延长线于点S；连接D1S，交AA1于点M，则五边形D1MENF即为所求作的截面图形。

由三角形相似可得A1M=3MA,CN=2NB，易得截面

作法 2（平行线法）：如图 2，连接 D1F，过 A作A1S//D1F，交 B1B 于点 S；过 E 作 EM//A1S，交 AA1于点 M，连接 D1M；过 C作 C1T//D1M，交 BB1于点 T；过F作FN//C1T，交BC于点N，则D1MENF五边形即为所求作的截面图形。

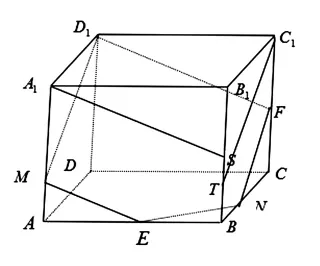
图2

点拨：作法1是通过延长线找线与线的交点，进而找出面与面的交线，最终找出截面与正方体各个面的交点；作法2是在正方体的表面不断地作已知直线的平行线，进而找出截面与正方体各个面的交点。

例2.已知正方体ABCD-A1B1C1D1的棱长为1，点P、Q、R 分别在棱 AB、BC、CD 上，且做出过P、Q、R三点的截面，并求出截面面积。

图3

作法：如图 3，由于 BP=BQ，所以 PQ//AC，那么过点R且平行于PQ的直线与AA1的交点U为AA1的中点，且点U在截面上，连接PU。因为UR的中点是正方体的中心，所以截面多边形的顶点关于正方体中心对称。由对称性，便可做出截面PQRSTU，且其面积为梯形积的2倍。

点拨：先利用平行线确认一个点在截面内，再利用正方体及截面的对称性，确认截面图形。

例3.已知正方体ABCD-A1B1C1D1的棱长为1，R、S、T 分别为棱 AA1、BC、C1D1的中点。求做过 R、S、T三点的截面，并且计算截面面积。

图4

作法 （辅助平面法）：首先过R、T做一个辅助平面。 过 T作 TG//D1D交于点 G，连接 A1T、AG，则有TG//A1A，得到辅助平面A1ATG。连接TR并延长交GA的延长线于点K。连接KS，交AB于点N，交DC的延长线于点E。连接ET，交CC1于点Q，交DD1的延长线于点F。 连接FR，交A1D1于点M，交KE于点H，则H必在DA的延长线上。最后，连接RN，SQ，TM，则六边形RNSQTM即为所求截面。

知△D1MT与△BSN， 因为 D1T=SB， 所以△D1MT≌△BSN，因此MT=NS。

又由R是A1A的中点，可证得KH=MT，KN=NE.又因为S是BC的中点，所以NS=SE.易证KH=HN=NS=SE。由此可得

同理可证得∠MTQ=∠TQS=∠QSN=∠SNR=∠NRM=∠TMR=120 ②

点拨：借助一个过其中两点的辅助平面，再利用延长线法找出截面与正方体各个面的交点。

闻师母病逝悲寄恩师周公

□ 陈则民

求学有缘遇周公，

爱徒如子胜亲翁。

园丁半世耕耘累，

笔墨终生教化丰。

退隐田庄刚快意，

携妻故里晚霞红。

悲闻师母西游去，

谁管周公老稚童？