小行星(58)Concordia测光研究∗
蒋攀飞王晓彬
(1中国科学院云南天文台昆明650011)
(2中国科学院天体结构与演化重点实验室昆明650011)
(3中国科学院大学北京100049)
1 引言
小行星是太阳系形成初期星子残留物.按照太阳系形成的星云坍缩理论,对在太阳系中处于特殊位置和具有特殊存在形态的小行星的物理参数研究,可以为太阳系早期演化条件提供证据,为小行星碰撞演化研究提供边界条件[1].主带小行星是行星科学重要的研究对象,主要有以下几个原因:它们是内太阳系行星形成早期阶段的星子的遗留物,在小行星上仍保留行星形成过程中的信息,例如,我们可以借小行星研究太阳系物质组成和形成类地行星的条件;它们可能发挥了将水和有机质带入地球的作用,曾经发生的与地球生物圈发生强烈作用,可能改变了生命形式进化的路径;小行星上蕴含的矿物质将来可以为人类提供可持续的资源[2−3].目前通过测光观测获得小行星自转轴在空间指向的只有几百颗[4],已经发现小行星数量有70多万颗之多,这离我们研究碰撞理论还相差很远.因此,研究具体小行星物理参量对于扩充小行星物理参量观测样本具有重要意义,有利于我们更好了解不同种类的小行星.
地基光学观测兼有技术和经济上的优势,观测的灵活性和观测时间长的特点,使得地面测光观测在小行星观测中发挥重要作用[5].光变曲线是获取小行星基本物理参数的主要来源.通常情况下,由于小行星地面观测呈点源星像,我们只能在不同的可视期通过小行星积分光度变化来推断小行星的形状、旋转状态和表面散射参数.自1906年Russel首次分析小行星反演问题,一个很自然而简单的想法就是研究小行星冲位置,然而,Russel得出一个十分悲观的结论:仅从冲时的光变曲线无法反演出3维形状和反照率变化.直到1953年,Cuffey首次运用椭球体反演小行星形状[6].此后,小行星基本物理参数的反演方法经历了从椭球体为基础的振幅法、星等法、振幅-星等法到凸面体反演方法的过程.Kaasalainen等[7]提出的凸面体反演方法可以有效获取小行星的恒星周期、形状和自转指向及表面散射性质等物理参量.
小行星的形状是一个重要的物理参量,形状记录了它们所经历的碰撞和地质演化.另一方面,比较不同种类小行星质量、密度、成分和角动量的分布时,形状也是重要因素[8].Torppa曾指出,小行星的自旋状态也受相互碰撞影响,导致观测到的极轴指向几乎随机分布[9].
小行星(58)Concordia是一颗C类主带小行星,直径92.19 km,周期9.895 h,目前仍没有其形状和轴指向信息.因此,我们利用云南天文台观测平台优势,在2000年和2015年对小行星(58)Concordia进行测光观测,通过凸面体反演方法1http://astro.troja.mff.cuni.cz/projects/asteroid3D分析其形状、自转周期和轴指向.
2 观测和数据处理
我们在2015年3月20日和3月21日利用云南天文台1 m望远镜对小行星(58)Concordia进行了测光观测, 所用CCD的像元素为2 k×2 k, 视场大小为7′18′′× 7′18′′, 观测时滤光片选择白光波段.利用IRAF(Image Reduction and Analysis Facility)软件包对获得的原始数据进行图像处理,主要包括本底、暗流、平场改正和剔除宇宙射线.利用APPHOT任务对目标源和比较星进行孔径测光.尝试不同孔径,选择光度测量精度最高的作为最优孔径,进而得到每个夜晚目标源和比较星的仪器星等.由于2015年3月20–21日这两天观测过程中有薄云,系统误差势必会产生影响,使用coarse de-correlation方法[10]和Tamuz方法[11]对观测目标的仪器星等中系统误差进行改正,从而改善数据的整体精度.
运用凸面体反演程序对23条光变曲线进行分析.所用观测数据的太阳相位角跨度从1.7◦到14.1◦,时间跨度为35 yr. 除了我们2000年12月22–24日观测获得的3条光变曲线外,其余光变曲线来自IAU-MPC(International Astronomical Union-Minor Planet Center)光变数据库和APC(Asteroid Photometric Catalog).具体有关观测信息见表1,表1从左至右依次列为小行星的观测时间(UTC)、地心距离、日心距离、太阳相位角、滤光片、数据来源和数据参考文献.
1981年测光观测数据采样稀疏,数据弥散较大.2006年有4个夜晚观测数据,数据弥散较大,2月4日、2月9日相位覆盖0.5个周期左右,变幅在0.1 mag左右,2月10日相位覆盖范围最小,2月13日观测数据采样较为密集,相位覆盖范围较大,变幅达0.14 mag.2007年3个夜晚观测数据的弥散较小,12月11日相位覆盖范围较小,其余两晚数据相位覆盖范围大,变幅变化在0.1 mag左右.2016年10天观测数据中,6月14日、17日、22日和7月4日数据弥散较小,变幅范围在0.1 mag左右,相位覆盖0.35–0.7个周期,其余数据较为弥散,相位覆盖0.5个周期左右,变幅变化为0.07–0.1 mag.

表1 (58)Concordia观测信息Table 1 The observation information for(58)Concordia
3 反演方法
凸面体反演方法在文献[16–17]中有详细描述.一般地,反演问题可描述为

在反演过程中,L为观测的小行星光亮度矩阵,A为与散射定律有关的系数矩阵,通常g为用高斯面密度表征的面元矢量.反演时存在解不唯一,可以通过假设小行星是凸面体来克服这一问题.在计算小行星积分光度时,假设小行星散射定律计算运用三角剖分方法得到的每个被太阳照亮且可视的面元上的光度,求和得到总的光度.通过比较模型光度与实测光度获得小行星自转参数和形状.具体地,利用最小二乘法得到待定参数的解,即:
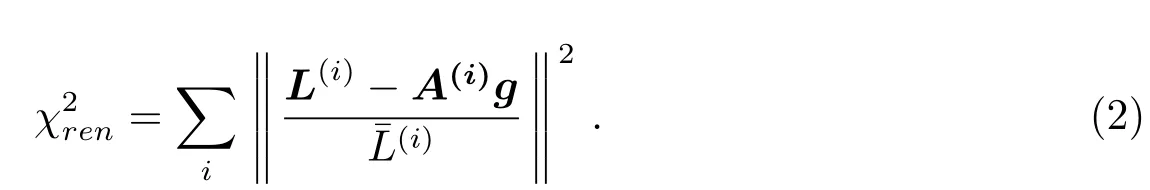
(2)式中上标i为光变曲线序号,¯L(i)为第i条光变曲线平均亮度.A(i)为第i条光变曲线与散射定律有关的系数矩阵,在得到每个面元的大小后利用闵可夫斯基最小化原理,重构小行星的具体形状,即获得每个面元的顶点.在凸面体方法反演时,为了得到全局最优解,我们进行了自转周期在一个范围的扫描分析以及自转轴在黄道球面坐标(λ,β)进行扫描计算.
4 反演结果
4.1 自转周期
Harris等人在1989年对(58)Corcondia进行首次测光观测,但是由于数据点较少且很疏散并未获得该小行星的会合周期[12],Gil-Hutton在1993年对小行星(58)Concordia测光观测推测,指出其会合周期不会小于16 h[18].Wang在2002年首次给出该小行星的可能会合周期为(9.90±0.01)h[13],Stephens[14]和Pilcher[15]分别在2006年和2016年对该小行星进行较长时间测光,根据光变曲线分别得到了会合周期为(9.895±0.002)h和(9.895±0.001)h.为了测定精确的小行星自转周期,我们对9.8–10 h区域进行周期值扫描,周期采样间隔为0.8∆P.

其中P为小行星自转周期,T为测光数据时间跨度.通过搜寻发现RMS(Root Mean Square)最小值在9.894541 h附近,对应RMS为0.012138.图1显示了在搜索范围内RMS分布情况.在对周期误差进行估计时,我们根据Kaasalainen等[17]和Torppa等[19]给出的典型周期误差范围0.01∆P−0.1∆P,对于(58)Concordia,其典型周期误差为1.6×10−6− 1.6× 10−5h.
4.2 自转轴指向
光度模型中的散射定律为Lommel-Seeliger和Lambert散射定律[17],由于所用测光数据多为相对流量,散射定律相关的参数设为固定值,a=0.5,d=0.1,k=−0.5,c=0.1.将扫描获得的自转周期作为初始值,进行轴指向和形状的精确测定.

图1 (58)Concordia周期与RMS对比Fig.1 The distribution of period vs.RMS
为了得到极轴的位置,Kaasalainen等[17]运用3轴椭球体模型拟合得到的轴指向作为初始轴指向.另外一种做法就是李彬等人采取文献[17]所提及的大范围搜寻法[20−21].在我们的工作中,考虑到光变曲线的条数和数据情况,并为了节省时间,将球谐函数的阶数设置为l=m=6.在初始轴指向选取方面,我们也采用了李彬等人所使用的方法,将整个轴指向空间划分成一个2◦×2◦的网格,初始轴指向处于网格的节点上,然后再运用自编程序实现自动生成输入文件,从计算结果中提取每次计算的局部最优解.从大量的局部最优解中挑选出可能的全局最优解为初值,将球谐函数的阶数设置l=m=8,最后找出最终的全局最优解.
图2是通过网格搜寻法所获得的局部最优解与χ2的分布图.根据遍历搜寻法的结果,我们得到了轴指向的全局最优解为λ=15.9◦,β= −1.4◦,其对应χ2=0.4979,我们还得到另外一组解,其轴指向为λ=197.4◦,β=+6.1◦,对应χ2=0.4952.对于其误差估计我们采用比较简单的方法,Torppa等人曾指出[19]:“改变不同的初始值、轴指向、散射参数会得到轴指向的分布”,根据经验,可行解的χ2大概在5%–10%左右波动,我们直接用5%的波动去进行估计,根据已有的结果,我们发现(58)Concordia的轴指向为λ1=15.3◦±0.7◦,β1= −4.2◦±2.6◦,另外一组解为λ2=195.9◦±1.0◦,β2=4.8◦±1.2◦.
4.3 形状模型
将上述得到的自转周期值和轴指向作为相应输入参数,并将球谐函数的阶数设置为l=m=8,从而获得最终形状.图3是我们从两个极轴解得到的形状模型,上排为第一个极轴的形状模型,从左至右分别是从x轴方向、y轴方向、z轴方向观察的形状,下排为第2个极轴的形状模型,从左至右观察方向与第一个极轴一致.
为了检查拟合效果,在图4中,我们给出了所用的23条观测光变曲线和模型值对比,其中α是指观测时刻太阳相位角,θ为视界角,θ0为太阳方向和小行星极轴方向夹角.

图2 (58)Concordia极轴指向的χ2分布Fig.2 The χ2 distribution of(58)Concordia pole orientation

图3 (58)Concordia凸面体形状Fig.3 The convex shapes of(58)Concordia
通过图4可以看出,模型光变基本上拟合了大部分的观测光变曲线,仅少部分点拟合得不是很好.例如,1981年8月3日数据可能是时间采样稀疏和数据本身误差比较大的缘故,比如说中间有两个点十分弥散,相位间隔不到0.1,然而其观测值的变化却大于振幅;2000年12月23日数据中第0.7相位没有拟合得很好,这可能是由于(58)Concordia的表面结构比较复杂,比如经历过碰撞之后表面存在“较大弹坑”,仅用凸面体模型很难完全反映这种非凸结构.
总的来说,从光变曲线特征来看,光变曲线形状不规则,反映小行星形状也不规则.光度模型反映了大部分光变特征,仍有一些细微的特征没有很好拟合,这需要引入非凸模型来实现进一步的反演.

图4 (58)Concordia观测光变曲线和模型光变曲线.散点为观测数据,红实线为模型光变曲线Fig.4 The observational and modeling lightcurves of(58)Concordia.The scattered dots are observed data,and the red solid lines are modeling lightcurves
5 结论
我们分析了云台1 m镜(58)Concordia的测光数据以及前人提供的测光数据,通过凸面体反演方法,我们得到以下结论:
(1)通过凸面体反演方法,我们得到了该小行星的恒星周期为9.894541 h,周期误差为±1.6×10−5h;其可能轴指向为λ1=15.3◦±0.7◦,β1= −4.2◦±2.6◦,λ2=195.9◦±1.0◦,β2=4.8◦±1.2◦,从β取值来看,我们并不能得知该小行星是顺旋转还是逆旋转.
(2)从形状模型来看:两个轴指向的形状均含有非凸结构,当轴指向为λ1=15.3◦±0.7◦,β1= −4.2◦± 2.6◦,小行星(58)Concordia的形状更不规则.
(3)通过对比模型光变曲线和观测光变曲线,所得小行星凸面体形状不能完全拟合所有光变特征.该小行星需要高精度测光数据以及引入非凸面体模型.另外,现有的观测数据多为相对流量,需要相位角跨度更大的绝对测量数据来实现该目标相位函数的测定研究.
致谢感谢云南天文台1 m望远镜工作人员的支持.

