DBSCAN聚类算法在Gaia-DR2中检测疏散星团的研究∗

徐守坤 王 超 庄丽华 高新华

(常州大学信息科学与工程学院常州213164)

1 引言

邻近疏散星团(距离比较近的疏散星团)给我们提供了研究天体物理学中一些问题的机会,譬如恒星演化、银河距离尺度、银河结构,因为它们的距离可以基于精确的三角视差数据直接确定[1−4].

那么我们的首要工作是检测出这些邻近疏散星团成员.要进行邻近疏散星团成员检测就需要恒星大数据(覆盖范围广、数据量大、多维度的恒星样本)和高效的成员检测方法.之前由于恒星大数据比较匮乏,很多学者只是针对特定区域(包含疏散星团的一个小区域)进行成员判定的研究,提出了一些成员判定方法,而这些成员判定方法能否用于在大数据中进行邻近疏散星团的成员检测有待验证.早期用于确定疏散星团成员的方法是Vasilevskis-Sanders方法(简称VS方法), 由Vasilevskis等[5]提出, 再由Sanders[6]在其基础上加以改进,Zhao等[7]又进一步提出了改进方案,使VS方法能处理不等精度的自行数据.VS方法的基本原理是假设成员星和场星的自行或者视向速度都符合高斯分布,然后用极大似然法估计高斯分布中的参数,再计算每一颗恒星的成员概率,通常认为成员概率大的恒星是成员星的可能性比较大[7].但是,有学者表示VS方法有一定的局限性[8],当成员星数量远小于场星时,效果可能不好,当成员星和场星在速度空间重合时,结果也可能不理想.另外,VS方法不适合处理高维数据(三维及以上),因为当数据维数增大时,需要确定的高斯模型参数的数量也会随之增加,计算将会变得繁琐[9].还有一点,我们发现VS方法只能用于仅存在一个疏散星团和场星的情况,因为它是基于混合高斯模型的聚类方法[10],当有多个疏散星团存在时,需要引入更多的高斯模型.因此,VS方法不适用于数据分布相对复杂的大数据.

后来,针对VS方法的局限性,Sampedro等[11]提出了一种改进方法.与VS方法不同的是该方法假设每颗恒星与高密度中心点之间的距离符合高斯分布,能够充分利用恒星的多个数据(自行、视向速度、位置、视差等),并且高斯模型参数的数量不会随着数据维数的增高而变多,因为它只需要计算距离的概率密度函数(高斯模型),因此,该方法在处理高维数据(三维及以上)时比较便利.但是,不足之处是该方法需要对数据进行模型假设(参数方法),另外,该方法还需要不断地迭代寻找恰当的高密度中心点,过程繁琐.

近期,Gao等[9,12]提出用一种在数据挖掘中比较经典的算法——DBSCAN聚类算法(Density-Based Spatial Clustering of Applications with Noise)[13]来确定疏散星团成员.Gao等[9,12]使用NGC 188所在天区内的1046颗恒星的三维运动学数据(两维自行和视向速度)确定了疏散星团NGC 188的成员星,通过对成员星的二维空间位置分布图(赤经和赤纬)以及颜色-星等图的分析,证实他们得到的成员星是可靠的.DBSCAN算法有两个很重要的输入参数(Eps和MinPts),Eps为邻域半径,MinPts为稠密区域的密度阈值.DBSCAN算法的原理可以总结为:随机访问数据集中的任意一个点,判断其Eps邻域内的点个数是否大于等于MinPts,如果符合条件的话,则该点为核心点,该点与其Eps邻域内的点形成一个小簇,再判断该核心点Eps邻域内的点是否为核心点,如果存在核心点的话,则将以这些核心点为中心的小簇合并成一个大簇,如此迭代,直到所有点都被访问过.与前面的成员判定方法相比,DBSCAN算法不做任何模型假设(非参数方法),因而可以发现任意形状的簇,同时可以比较便利地处理三维及以上的高维数据.

目前,新一代的恒星大数据已经发布——Gaia Data Release 2(Gaia-DR2)[14].基于Gaia-DR2星表[14],我们获取了距离太阳小于100 pc的594284颗恒星样本,用恒星的五维数据(三维空间位置和两维自行)构建了一个五维相空间,以Gao等[9,12]针对特定区域进行成员判定的工作为基础,我们尝试采用DBSCAN算法进行距离太阳100 pc区域内的邻近疏散星团成员检测.

2 数据与方法

2.1 数据

我们的疏散星团成员检测工作需要高精度的天体测量数据,Gaia-DR2的发布给我们提供了机会.Gaia-DR2是欧洲航空局公布的Gaia卫星的第2期数据,Gaia卫星的科学目标是阐述银河系的组成与演化[15].Gaia-DR2中包含了13亿颗恒星的位置、视差和自行数据以及17亿颗恒星的测光数据,视差和位置数据的误差大概是0.3 mas,自行的误差大概是0.7 mas·yr−1[14,16].我们从Gaia-DR2星表[14]中选取了距离太阳100 pc以内的594284颗恒星样本,通过计算,我们发现:在100 pc处0.3 mas的视差误差仅会导致3 pc的距离误差,可用以下误差传递公式[17]计算:

其中,σd是距离误差,表示太阳与恒星之间的距离d对视差π求导,距离与视差的关系由(2)式给出,σπ表示视差π的误差.因此,我们选取的594284颗恒星样本的数据精度较高,满足DBSCAN算法对于数据精度的要求.利用位置和视差数据,计算了每颗恒星在三维位置空间中的坐标,坐标中心为太阳,用(α,δ,π)分别表示恒星的赤经、赤纬、视差,那么恒星在以pc为单位的三维位置空间中的坐标(X,Y,Z)可以用以下公式[18]计算:

图1为样本中594284颗恒星在三维位置空间中的分布图.

图1 594284颗恒星样本的三维位置空间分布图.太阳(蓝点)位于三维位置空间的中心Fig.1 The distribution of 594284 sample stars in a 3D position space.The Sun(blue point)is located in the center of the 3D position space

最终,我们可以使用594284颗恒星的三维空间位置以及两维自行数据来进行疏散星团成员检测.由于我们的实验需要计算恒星之间的欧氏距离,而三维位置数据和两维自行数据的单位是不一致的,为了避免某一维数据在计算距离时占据主导地位(不同单位的数据的值域是不一样的),我们将每一维数据标准化到[0,1]区间内,采用以下公式[19]进行处理:

其中,x表示初始数据,min(x)和max(x)分别代表初始数据的最小值和最大值,x′表示标准化后的无量纲值.

2.2 参数确定

(Eps,MinPts)是DBSCAN算法的2个非常重要的输入参数,它们的选取会直接影响到我们的聚类效果[20−21].Ester等[13]提出用k-dist图确定DBSCAN算法的输入参数,并且他们已经证实k-dist图在二维数据中的可行性,我们尝试将它应用到五维数据集中.k-dist图就是用按k-dist值(每个点与它的第k个最近邻之间的距离)排序后的点编号和排序后的k-dist值绘制的曲线图.绘制曲线之前,我们需要计算每个点与其他点的欧氏距离.对于我们所使用的594284颗恒星样本,我们用以下公式计算每颗恒星与其他恒星之间的距离:

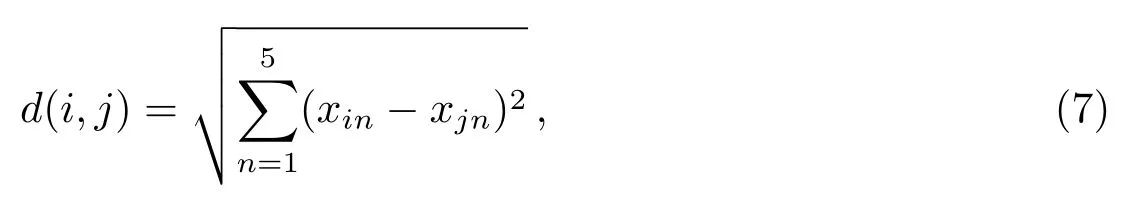
其中,d(i,j)表示第i颗恒星与第j颗恒星之间的距离,n表示数据维数,xin与xjn分别表示第i颗恒星与第j颗恒星的第n维数据.假设恒星总数为N,就会得到N个包含N−1个距离值的序列,然后将序列按升序排序,得到每颗恒星的距离序列[22],最后绘制k-dist图.图1就是我们绘制的恒星样本的k-dist图,为了便于观察,对于每个k,我们都取排序后的前800个k-dist值.

通过观察图2,我们发现当k取到9之后,曲线开始趋于稳定,其中的原因是随着k的增大,成员星的k-dist值变化很缓慢,而场星的k-dist值变化则比较快[9],当k取到9之后,成员星的k-dist值基本都小于场星.考虑到恒星本身以及它的9个近邻,因而我们取MinPts=10.再观察图3(恒星样本的9-dist值图),我们发现蓝色虚线正好将曲线分成两部分,虚线两侧数据变化趋势明显不同,并且左侧数据明显少于右侧数据,符合成员星与场星的数量差异,因此,我们暂且将虚线左侧全部取为成员星,虚线右侧取为场星.此时,蓝色虚线是成员星与场星的9-dist值的分界处,所以我们取Eps为虚线处的9-dist值,即Eps=0.0023.

2.3 成员检测

根据k-dist图我们得到了DBSCAN算法的两个输入参数,Eps=0.0023,MinPts=10.从图3中我们发现虚线左侧大概包含150个k-dist值,依据k-dist图的原理[13],虚线左侧的150个k-dist值包含核心点与边界点,按照核心点和边界点的定义[13],我们知道核心点是高密度的点(Eps邻域内包含的点个数大于等于MinPts),可以选为成员星,而边界点是比较特殊的一类点,它们位于核心点的Eps邻域内,但自身Eps邻域内的点个数少于MinPts,为此,我们画出了核心点与边界点的自行矢点图(图4).通过观察,我们发现两组核心点的自行各自是相近的,部分边界点的自行与核心点相差较大,并且分布比较分散,不符合成员星自行相近的特点,因此,我们将这部分不符合成员星特征的边界点(图4中黄色矩形框内的点)排除掉,保留核心点和剩下的边界点,最终得到135颗候选成员星.如图5和图6所示,我们使用DBSCAN算法一共检测到两个疏散星团,根据成员星的赤道坐标(赤经与赤纬)和三角视差对应的距离,我们确定这两个疏散星团为Hyades和Coma.图5为候选成员星的三维空间分布图,图中显示两个疏散星团的成员均位于高密度区域,需要说明的是,从恒星样本的三维位置空间分布图(图1)可以看出,样本中恒星数量过大,而成员星数量远小于场星,在三维位置空间中,大量的场星会遮挡住成员星,因此,我们只画出候选成员星的三维空间分布图.图6为候选成员星与场星的自行矢点图,图中两个疏散星团成员的自行是各自相近的,只有个别孤立的点可能是混入的场星.依据候选成员星与场星的自行矢点图(图6),我们剔除掉两颗很有可能是场星的候选成员星(图中红色矩形框内的点)之后,共得到133颗成员星,其中95颗属于Hyades,另外38颗属于Coma.图7为我们画出的成员星与场星的二维空间分布图,图中两个疏散星团成员都是各自成团的,说明我们得到的成员星是可靠的.另外,图8和图9分别为Coma和Hyades成员星的颜色-星等图,两幅图均清晰地显示了星团主序,进一步证实了我们获取的成员星的可靠性.

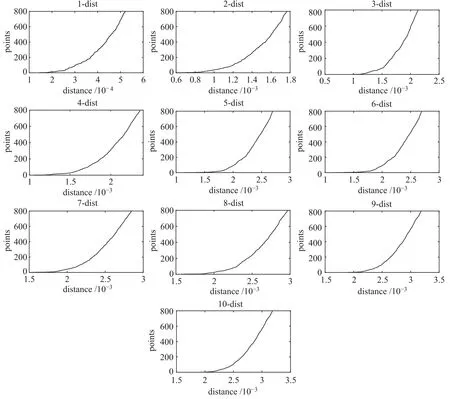
图2 594284颗恒星样本的k-dist图(k=1,2,3,4,5,6,7,8,9,10)Fig.2 The k-dist graphs of 594284 sample stars(k=1,2,3,4,5,6,7,8,9,10)

图3 恒星样本的9-dist图.蓝色虚线是成员星与场星的分界处Fig.3 The 9-dist graph of sample stars.The blue dashed line is the border of the members and field stars

图4 核心点(红点)与边界点(蓝点)的自行矢点图.黄色矩形框内的点为排除掉的点.pmRA与pmDEC分别为赤经和赤纬方向上的自行Fig.4 The proper-motion vector point diagram of the core points(red dots)and border points(blue dots).The points in the yellow rectangles are the points which are excluded.pmRA and pmDEC are proper motions in the right ascension and declination directions,respectively

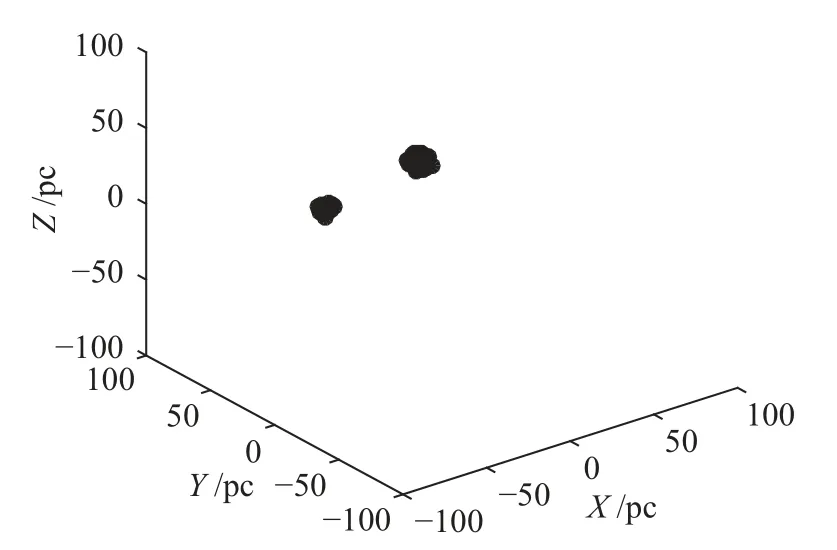
图5 135颗候选成员星在三维位置空间中的分布情况Fig.5 The distribution of 135 candidate members in the 3D position space

图6 135颗候选成员星(红点)与场星(黑点)的自行矢点图.蓝色和黄色椭圆区域分别代表Hyades和Coma的成员星.红色矩形框内的点为混入的场星.pmRA与pmDEC分别为赤经和赤纬方向上的自行Fig.6 The proper-motion vector point diagram of the 135 candidate members(red dots)and field stars(black dots).The blue and yellow ellipse represent the members of the Hyades and Coma clusters,respectively.The red rectangle represents the field stars mixing into the members.pmRA and pmDEC are proper motions in the right ascension and declination directions,respectively

图7 成员星(红点)与场星(黑点)的二维空间分布图.蓝色和黄色椭圆区域分别代表Hyades和Coma的成员星Fig.7 The 2D projected spatial distribution of members(red dots)and field stars(black dots).The blue and yellow ellipse represent members of the Hyades and Coma clusters,respectively

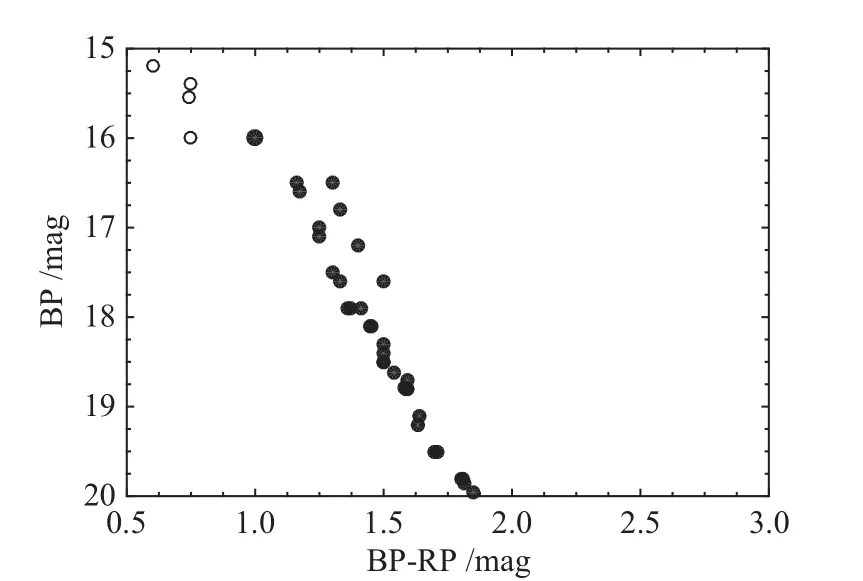
图8 38颗Coma成员星的颜色-星等图.黑点和圆圈分别为核心点与边界点.BP与RP是恒星的两种照相星等,BP-RP为恒星的颜色Fig.8 The color-magnitude diagram of the 38 members of Coma cluster.The black dots and circles are the core and border points,respectively.BP and RP are two types of photo magnitude of stars.BP-RP is color of stars

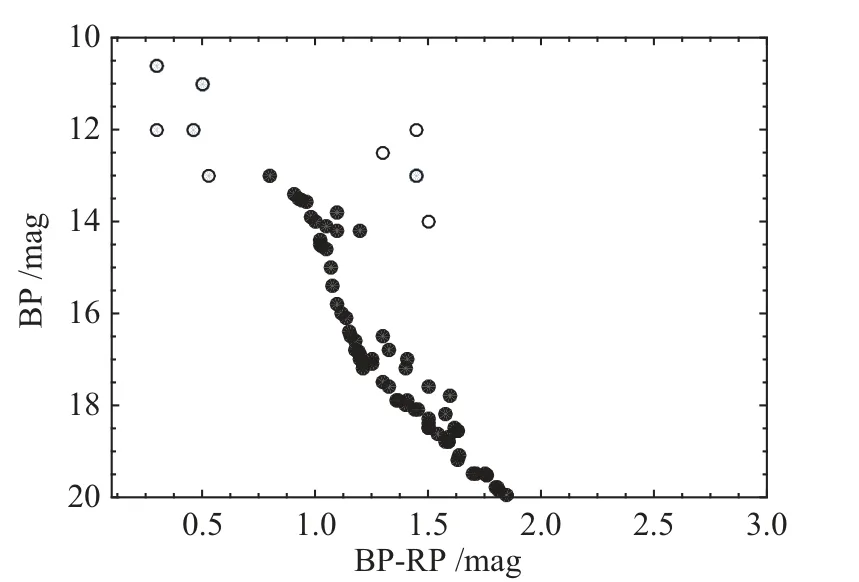
图9 95颗Hyades成员星的颜色-星等图.黑点和圆圈分别为核心点与边界点.BP与RP是恒星的两种照相星等,BP-RP为恒星的颜色Fig.9 The color-magnitude diagram of 95 members of Hyades cluster.The black dots and circles are the core and border points,respectively.BP and RP are two types of photo magnitude of stars.BP-RP is color of stars

2.4 星团距离

获取了可靠成员星之后,我们利用Gaia-DR2中的视差数据重新确定了两个疏散星团的距离.我们选取的594284颗恒星样本中绝大多数恒星(大约93%)的视差数据的相对误差(σπ/π)<0.2,图10为594284颗恒星视差的相对误差分布情况.

图10 距离太阳100 pc以内的594284颗恒星视差的相对误差分布Fig.10 The relative parallax errors of 594284 sample stars within a distance of 100 pc to the Sun

我们先根据成员星的视差和视差的误差分别计算了两个星团的加权平均视差,通过以下公式[18]计算:

其中,wi表示第i颗成员星的权值,πi和σπi分别表示第i颗成员星的视差以及视差对应的误差,和分别表示星团的加权平均视差和对应的误差,S表示星团的成员星数量.根据星团的加权平均视差和对应的误差,我们可以算出星团的距离和对应误差可以用以下公式[18]计算:

最终,Hyades的视差确定为(21.51±0.10)mas,对应的距离为(46.5±0.3)pc,Coma的视差确定为(11.77±0.06)mas,对应的距离为(84.9±0.4)pc,我们确定的星团距离与之前Gao[18]计算的结果基本一致.

3 结论与讨论

在本文中,我们借鉴Gao等[9,12]针对特定区域的疏散星团成员判定工作,将DBSCAN算法拓展到恒星大数据中进行成员检测.基于Gaia-DR2星表,为了获得更加可靠的成员星,我们使用恒星的五维数据(三维空间位置以及两维自行)进行检测.考虑到位置数据和自行的单位不一致,为了得到更好的聚类效果,我们就将每一维数据标准化到[0,1]区间内.借助k-dist图,我们确定了DBSCAN算法的输入参数(Eps,MinPts),证实了k-dist图在高维数据(三维及以上)中的可行性.最终,我们在距离100 pc范围以内的594284颗恒星中检测到133颗可靠成员星,它们被分成两组(Hyades和Coma),证实了DBSCAN算法在邻近疏散星团成员检测上的可行性.

DBSCAN算法是一种基于密度的聚类算法,它通过统计每个点邻域内的点个数来确定该点的密度,不像VS方法这样的参数方法需要对数据进行模型假设,因而它可以发现任意形状的簇,另外,它也不需要复杂的数学计算,适用于高维数据的聚类,所以,我们可以将它用于大数据中的五维相空间成员检测.近期,天文学家逐渐意识到DBSCAN算法的潜力,继Gao等[9,12]首次将它用于疏散星团成员判定之后,Castro-Ginard等[23]提出用一种将DBSCAN算法与神经网络相结合的方法进行疏散星团成员检测,他们将该方法应用到Tycho-Gaia Astrometric Solution(TGAS)[24]数据中,并用Gaia-DR2中的测光数据验证该方法的可靠性,在他们的实验中,他们也是使用的五维数据(二维位置、视差以及两维自行)进行检测,但他们没有对五维数据进行标准化处理(五维数据的单位是不一样的).而本文的工作与Castro-Ginard等[23]做的并不一样,我们是直接从Gaia-DR2星表中选取了距离100 pc以内的恒星样本,利用样本中的位置和视差数据计算得到每颗恒星的三维空间位置,再结合样本中的两维自行数据,总共五维数据用于成员检测,在用DBSCAN算法聚类之前,对五维数据进行了标准化处理,最后用二维空间位置(赤经和赤纬)和颜色-星等图对所得的成员星进行了验证.此外,值得一提的是,DBSCAN算法不仅可以用于疏散星团成员的确定,还具备在较大的数据空间中发现未知高密度结构的能力,近期Bhattacharya等[25]通过DBSCAN算法分析了疏散星团Czernik 20和NGC 1857的空间形态特征,发现一个先前未知的超密结构.需要指出的是,DBSCAN算法也有它的缺陷,在确定疏散星团成员时,它无法计算出每一颗恒星的成员概率,而且对数据精度的要求较高,另外,由于DBSCAN算法的两个输入参数(Eps和MinPts)是针对全局数据的,当数据集中数据分布不均匀时(存在多个密度相差较大的簇),有些相对松散的簇可能会被遗漏掉,因此,在距离太阳100 pc以内区域中,除了我们检测到的两个疏散星团,可能还存在着其他星团.

致谢 感谢审稿人提出的宝贵意见以及编辑的辛苦工作.