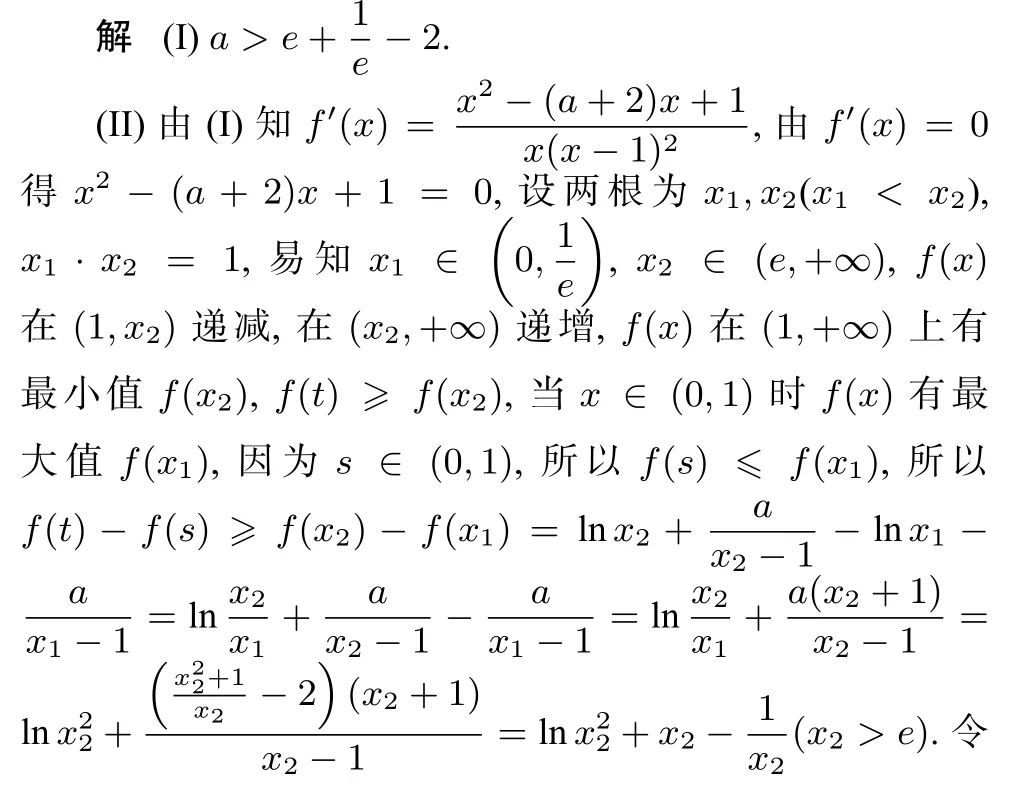探寻中间量 “天堑”变通途—导数不等式证明的策略探究

安徽省池州市第一中学(247000) 吴成强

全国卷最后一道压轴题常常是导数题,对考生的能力特别是创新能力有较高要求,对优秀学生具有选拔功能,是试卷具有较高区分度的一道把关题.这道题考查的范围比较广,其中导数不等式证明问题常常被考查.不等式的证明,一般来说灵活性强,难度较大,需要考生熟练的掌握基本方法和基本技巧,具有较为扎实的数学功底和较高的数学素养,对考生综合运用知识解决问题的能力,特别是在新的情境下实现知识有效迁移的能力有较高要求.有些不等式的证明,命题者在设计的时候就是有意要求考生能先探寻一个中间量,通过中间量做一个跳板进行过渡转换,把原不等式中条件到结论“大跨度”降低为“小跨度”,即把原不等式改为一个易于证明的加强不等式,使证明难度大大降低.如何探寻到一个合适的“中间量”,这是破解这类问题的关键之所在、策略之所在.这些“中间量”往往比较隐含,不太容易发现,所以我们要加强这方面的研究,积累这方面的经验.当然,我们还需要数学的直觉,灵感的迸发,敏锐的观察,严密的推理,更需要较高的创新能力和灵活应变能力.

一、通过消元策略探寻中间量

在一个式子中如果有多个变量,我们首先要把这些变量之间的关系找出来,然后选择一个合适的变量,用这个变量表示其它变量,将多元变量化为单元变量.再抓住式子的结构特征,选择一个合适的中间量,以这个中间量作跳板进行过渡,把原来一个跨度大、坡度陡、弯子急的问题降低为跨度小、坡度缓、弯子小的问题,即得到一个加强不等式,从而把原不等式的证明改为加强不等式的证明,使证明的难度大大降低.

(II)求证:f(x1)+f(x2)＞2.

解析(I)a的取值范围为(1,+∞).

(II) 由(I)知,x1,x2为g(x)=f′(x)=ex-x-a=0的两个实数根,设x1＜0＜x2,g(x)在(-∞,0)上单调递减.下面先证x1＜-x2＜0,只需证g(-x2)＜g(x1)=0.因为g(x2)=ex2-x2-a=0,得a=ex2-x2,所以g(-x2)=e-x2+x2-a=e-x2-ex2+2x2.设h(x)=e-x-ex+2x,x＞0,则h′(x)=-e-x-ex+2＜0,所以h(x)在(0,+∞)上单调递减,所以h(x)＜h(0)=0,所以h(x2)=g(-x2)＜0,所以x1＜-x2＜0(发现了两个变量x1,-x2之间的大小关系)因为函数f(x)在(x1,0)上也单调递减,所以f(x1)＞f(-x2),f(x1)+f(x2)＞f(-x2)+f(x2)(将不等式进行放缩,得到中间量.)所以要证f(x1)+f(x2)＞2,只需证f(-x2)+f(x2)＞2,即证(将二元变量化为单元变量.)设函数k(x)=ex+e-x-x2-2,x∈(0,+∞),则k′(x)=ex-e-x-2x.设φ(x)=k′(x)=ex-e-x-2x,则φ′(x)=ex+e-x-2＞0,所以φ(x)在(0,+∞)上单调递增,所以φ(x)＞φ(0)=0,即k′(x)＞0.所以k(x)在(0,+∞)上单调递增,所以k(x)＞k(0)=0.所以当x∈(0,+∞)时,ex+e-x-x2-2＞0,则所以f(-x2)+f(x2)＞2,所以f(x1)+f(x2)＞2.

评注本题中首先要善于发现两个变量x1,x2之间的大小关系,利用x1＜-x2＜0,得到f(x1)＞f(-x2),将原不等式转化为加强不等式f(-x2)+f(x2)＞2,这个加强不等式的证明比原不等式的证明要容易的多.本题中的中间量是:f(-x2)+f(x2).

二、通过基本不等式放缩策略探寻中间量

例2已知函数f(x)=e2x-2mex+4(lnx)2-4mlnx+2m2,求证:对任意的x＞0,m∈R,恒有f(x)＞4-2ln2.

文中针对热电偶传感器特性及弱信号检测的特点，研究弱信号检测及降噪处理方法，采用多级放大、软件滤波等手段，提高系统检测精度，滤除信号干扰，进而确保对空间晶体生长炉温度进行更为稳定的控制。

证明f(x)=(ex-m)2+(2lnx-m)2,即证(ex-m)2+(2lnx-m)2＞4-2ln2,由不等式可得

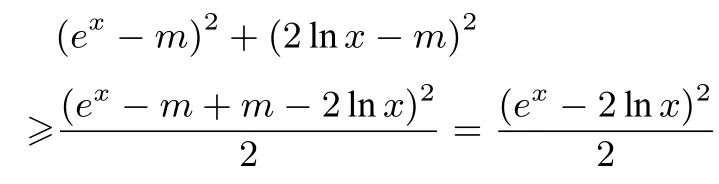
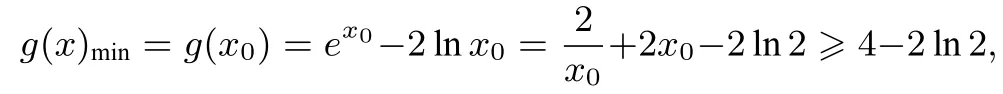
所以对任意的x＞0,m∈R,恒有f(x)＞4-2ln2.

评注本题就是巧妙地运用基本不等式把原来比较复杂的不等式(ex-m)2+(2lnx-m)2＞4-2ln2的证明转化为比较简单的加强不等式的证明,这确实是一个比较高明的想法,体现了思维的灵活性.我们在解决问题的时候不能一条道走到黑,应该审时度势,灵活应变,多角度、多层次、宽领域的进行探究,探求出最佳、最简、最有智慧的解法.

例3已知函数若方程f(x)=1有两个不相等的实数解x1,x2,证明:x1+x2＞2e.

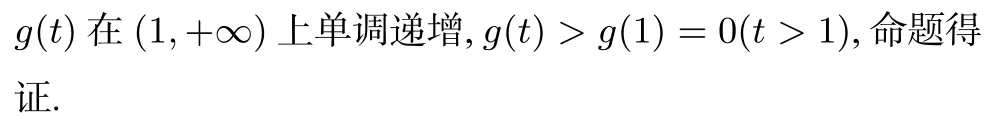
评注本题就是巧妙地运用基本不等式把原来比较难证的不等式x1+x2＞2e的证明转化为比较简单的加强不等式x1·x2＞e2,即lnx1+lnx2＞2的证明.这也是比较好的解法,体现了转化与划归思想的灵活运用,即化难为易,化繁为简.

例4已知函数f(x)=ae2x+bex(a0),g(x)=x,若函数F(x)=f(x)-g(x)有两个不同的零点x1,x2,记对任意a∈(0,+∞),b∈R,试比较f′(x0)与g′(x0)的大小,并证明你的结论.

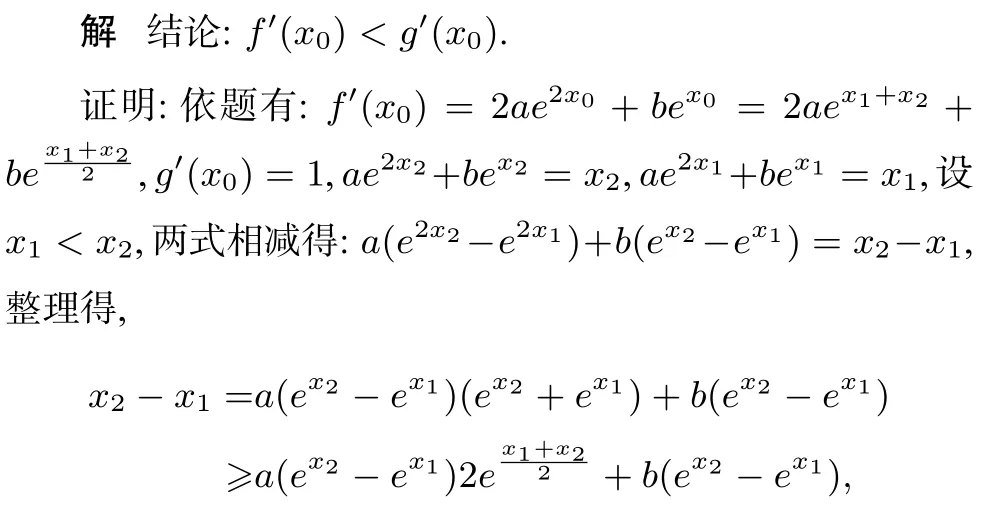
评注本题也是巧妙地运用基本不等式得到不等式这一步是整个问题能够顺利求解的关键和核心之所在,如果不作这样的转化,那么原问题的求解将是山穷水复疑无路,但作了这样的划归后就是柳暗花明又一村.

三、利用“重要结论”探寻中间量

数学中有许多重要结论,这些结论展现了数学的魅力之所在,往往令人感到无比的震撼.例如导数中最为常用的结论有:ln(1+x)≤x,ex≥1+x,这两个重要结论在高考试卷中已被多次考到.解题中如果我们能恰当地运用这两个结论,这将对我们解题会提供一个很好的思路引导,也会使问题求解变得十分简单.

例5求证:ex＞ln(x+2).

证明易证:ex≥x+1(等号成立的条件是x=0),x+1≥ ln(x+2)(等号成立的条件是x=-1),所以ex＞ln(x+2).

评注本题也是巧妙地运用了重要结论ex≥1+x,ln(1+x)≤x,使证明变得十分简单.倘若不知道运用这些结论,问题的求解就会变得复杂的多.教学实践中,发现一些学生不善于运用这些结论,结果他们费了很大的劲都没有证出来.可见这些重要结论对我们解题有很大的帮助,正如我经常跟学生强调的:记住有关结论,就能提高我们解题的起点.另外,我们还容易看到,直线y=x+1是函数y=ex与函数y=ln(x+2)的“隔离直线”,将两个函数隔离开来,函数y=ex的图像在直线y=x+1的上方,函数y=ln(x+2)在直线的下方,两者的大小关系一目了然.本题的中间量是x+1.

例6证明:当x＞0时,x2+x＞2lnx+2sinx.

证明当x＞0时,x-1≥lnx(重要结论到简单变形式.)所以要证明x2+x＞2lnx+2sinx,只需证明x2+x＞2(x-1)+2sinx,即证x2-x+2＞2sinx(将lnx放大为x-1,得到加强不等式.)当x＞1时,恒有2sinx≤2＜x2-x+2;当0＜x≤1时,设g(x)=x2-x+2-2sinx,则g′(x)=2x-1-2cosx,因为g′(x)在 (0,1]上单调递增,且所以g′(x)＜0,g(x)单调递减,所以g(x)≥g(1)=2-2sin1＞0,即x2-x+2＞2sinx.综上可得x2+x＞2lnx+2sinx.

评注本题中利用重要结论x-1≥lnx,将原不等式x2+x＞2lnx+2sinx的证明改为加强不等式x2-x+2＞2sinx(x＞0)的证明,这就变得容易的多了,但这种方法学生不一定能想到,所以在平时的训练中要强化这种意识,形成思维的自觉性,提高思维的起点.本题的中间量为:2(x-1)+2sinx.

四、利用“隔离”的策略探寻中间量

在比较两个函数大小的时候,我们常常找出一条直线(或其他函数),将已知的两个函数图像隔离开来,一个函数的图像在直线的上方,另一个函数的图像在直线的下方,这样两个函数的大小的比较就一目了然了.这条隔离直线通常是两个函数的切线.

例7已知函数在x=1处的切线方程为:ex-4y+e=0.

(I)求m,n的值;

(II)当x＞0且x1时,求证:

解(I)易得m=n=1.

评注本题由(I)知函数在x=1处的切线为:ex-4y+e=0,这条切线就是函数与函数的隔离直线,易证得从而容易证明原不等式成立.本题的中间量为:

五、由“最值”探寻中间量

在比较两个函数大小的时候,我们还常常考虑两个函数的最值,若一个函数的最大值不大于另一个函数的最小值,那么这两个函数的大小关系就一目了然了.这种比较一个函数的最大值与另一个函数最小值的方法是比较两个函数大小的一个很重要的方法,值得我们细细品味和牢固掌握.

例8已知函数

(I)若函数f(x)在(e,+∞)有极值,求实数a的范围;

(II)在(I)的条件下,对任意t∈(1,+∞),s∈(0,1),求证: