2018年高考全国I卷“函数与导数”试题分析与备考建议*

广东省惠州市第一中学高中部(516007) 李晓波 方德兰

高中数学主干知识包括函数与导数、数列、三角函数、立体几何、解析几何、概率与统计,这些主干知识构成了高考数学试卷的主体.其中函数与导数是重中之重,在其它主干中都可以找到它的影子.

今年全国I卷“函数与导数”试题突出重点内容重点考查,即使近几年都考过,也不回避,比如函数的性质(包括函数单调性,奇偶性,对称性,周期性等),零点问题,前两年考了今年照样考,百考不厌,常考常新！试题从整体角度、系统高度考查学生的综合素养.事实上,“函数”始终贯穿高中数学的函数和方程、分类讨论、数形结合、转化与化归等数学思想的教学主线,可以很好的考查学生的数学思维能力,计算能力,数学思维的严谨性与发散性,是为高校选拔人才的重要载体.

一.2018年全国I卷“函数与导数”试题评析

(一)理科数学“函数与导数”试题评析

题目1(全国I卷理科第5题)设函数f(x)=x3+(a-1)x2+ax.若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为( )

A.y=-2xB.y=-xC.y=2xD.y=x

评析此题比较简单,考查函数的性质与利用导数工具求切线方程,充分体现了命题者考基础,考概念的基本思路.

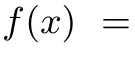
A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞)

评析此题重点考查基本初等函数的图像,要求考生掌握数形结合与转化思想,该题参数的位置决定了试题的难度不大,充分体现了命题者的人文关怀.

题目3(全国 I卷理科第21题)已知函数f(x)=

(1)讨论f(x)的单调性;

(2)若f(x)存在两个极值点x1,x2,证明:

评析考虑到是压轴题,有“把关”的作用,我们予以重点解析.今年的函数压轴题的表述与往年类似,简明而清新,不在题面上绕来绕去,但要求学生有较好的函数基本功.第一问不难,考查含参函数的单调性问题.以下对第二问进行解法分析.

解法一(化为关于x2(或x1)的一元函数不等式问题.)

由(1)知,f(x)存在两个极值点当且仅当a＞2.由于f(x)的两个极值点x1,x2满足x2-ax+1=0,所以x1x2=1.不妨设x1＜x2,则x2＞1.由于

说明此解法较好的利用x1x2=1条件把二元问题,转化为一元函数不等式问题,再利用其单调性进行证明.这应该是最多考生采用的方法,比较简洁.也可以把多元问题转化为关于x1的一元不等式问题,后面构造函数时也可以略有不同,其本质一样,就不作为新的解法了.

解法二(利用对数平均不等式)

由(1)知,f(x)存在两个极值点当且仅当a＞2.由于f(x)的两个极值点x1,x2满足x2-ax+1=0,所以x1x2=1.

不妨设0＜x1＜x2,则只需证:

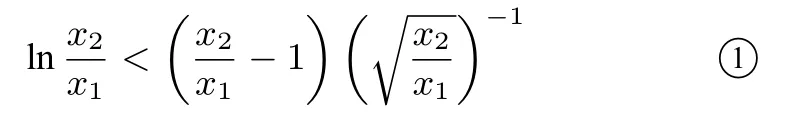
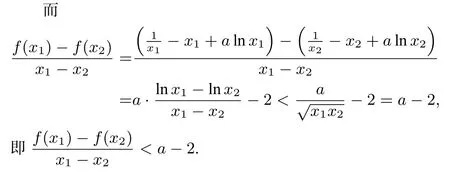
说明此方法先证明对数平均不等式:再利用其进行证明原不等式,清新而自然.

解法三(转化为关于a的一元函数不等式问题)

由 (1)知,当a＞2时,有两个极值点x1,x2,且注意到,

说明事实上,因为x1,x2是两个极值点,所以它们均可以被a表示,可以转化为关于a的一元不等式问题,然后利用函数单调性进行证明.

此题较好的考查了学生“消元”的思想,构造辅助函数,把不等式的证明转化为利用导数研究函数的单调性和求最值,从而证得不等式,好题！

(二)文科数学“函数与导数”试题分析

题目4(全国I卷文科第6题)设函数f(x)=x3+(a-1)x2+ax.若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为( )

A.y=-2xB.y=-xC.y=2xD.y=x

评析本题与理科第5题完全一致,不再赘述.

题目5(全国I卷文科第12题)设函数

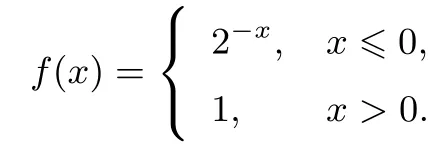
则满足f(x+1)＜f(2x)的x的取值范围是()

A.(-∞,-1] B.(0,+∞) C.(-1,0) D.(-∞,0)

评析分段函数是全国卷的宠儿,此题考查学生的分类讨论思想和数学结合思想.事实上,如果注意到分段函数中,当x＞0时函数的取值始终是一个常数,甚至可以不动笔而得到答案.

题目6(全国I卷文科第 13题)已知函数f(x)=log2(x2+a).若f(3)=1,则a=____.

评析本题考查学生对数的运算,属于容易题.

题目7(全国 I卷文科第21题)已知函数f(x)=aex-lnx-1.

(1)设x=2是f(x)的极值点,求a,并求f(x)的单调区间;

评析本题延续全国卷函数压轴题表述简明清新的特点,且入手容易,拾级而上.第一问让多数学生有思路并拿到分数,第二问是全国卷的典型特色,设计成以指数函数(或对数函数)与多项式组合,添加一个可能需要讨论的参数,构建了一个函数不等式的证明问题.我们对第二问进行解法分析.

解法一(先处理参数)

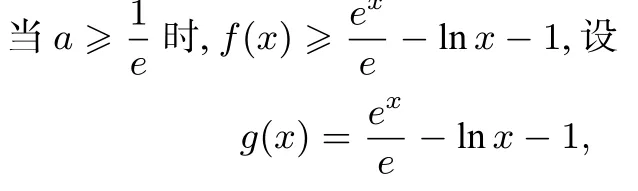
说明观察题目可发现,参数a的范围是明确的,所以容易想到先把a放缩掉,再证明函数不等式成立即可.

解法二(“参变分离”)

由于x＞0,ex＞1,当要证f(x)≥ 0,只需证设

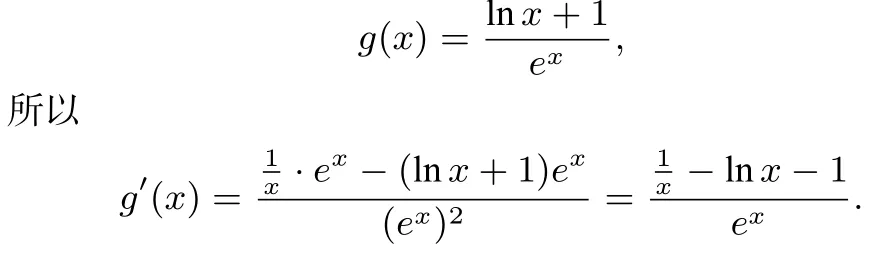
说明不等式进行“参变分离”后,即转化为求一个不含参的新函数的最值问题,再把这个最值与a进行比较即可.

解法三(利用“经典不等式”放缩证明)

说明这可能是此题最简洁的方法,利用两个经典不等式放缩证明,漂亮！

二.近三年全国I卷“函数与导数”考点分析

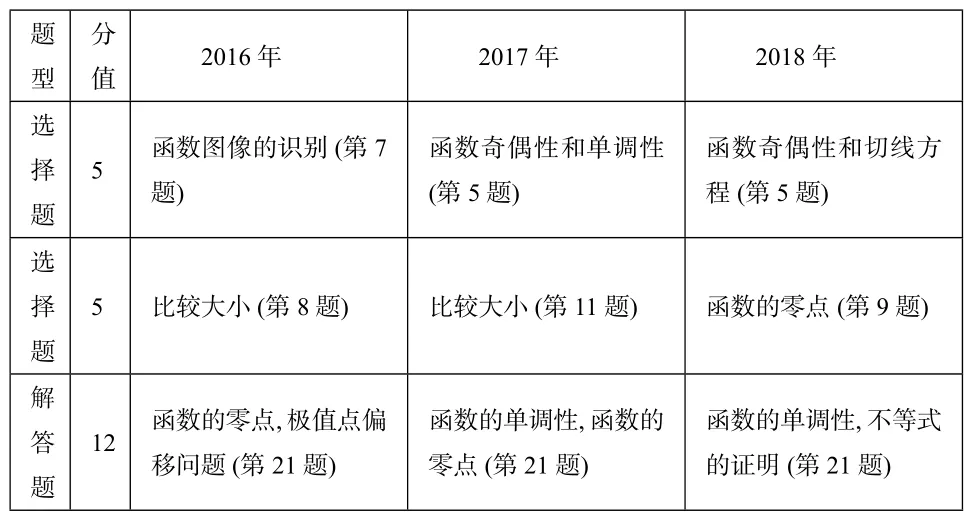
表1:近三年全国I卷“函数和导数”试题考点与分值统计表(理科)

表2:近三年全国I卷“函数和导数”试题考点与分值统计表(文科)

通过对近三年全国I卷“函数与导数”试题的分析(详见考点与分值统计表),可以发现,全国I卷对“函数和导数”内容的考查相当稳定！理科是“一大两小共22分”,文科是“一大三小共27分”,客观题考查函数的图像、性质、零点,曲线的切线方程等基本问题,在考基础、考通性、考通法上试题体现得浓墨重彩,淋漓尽致,呈现出“入手容易、阶梯递进、拾级而上”的特点,体现了“题在书外、理在书中”的特色.解答题位置固定在第21题,有“把关、压轴”之意.近年来难度略有下降,题目采用多问递进的设问方式,从易到难,区分度明显,采分点明确.其命题特点是以幂指对式和含参的二次三项式、含参的分式组成的函数为载体,常考不等式恒成立时逆求参数的取值范围(或最值),或者函数不等式证明问题.通常需要构造辅助函数,把不等式的证明转化为利用导数研究函数的单调性来求最值,从而证得不等式[1].

三.备考建议

1.回归课本,重视概念

课本是最重要的教学资源,也是高考命题的源头,从全国卷的命题特点来看,我们要重视课本,要重视课本中例题与习题的示范作用,让学生能熟练运用课本知识解决“基础题”,养成从课本中基本概念出发思考和解决问题的习惯,而不是过度地依赖教辅资料.在高考备考中,我们老师的主要任务就是让学生系统掌握课本知识,形成良好的数学认知结构.[2]

《普通高中数学课程标准(实验)》明确指出:“高中数学课程应该返璞归真,努力揭示数学概念、法则、结论的发展过程和本质.”[3]概念是解题的出发点与归宿,是构建数学理论大厦的基石,是提高解决问题能力的前提,是数学学科的灵魂和精髓.但在实际的教学中,我们有的老师不讲基本概念或者随便一带而过,喜欢一味的钻难题,这可能是与学生过不去,也是与自己过不去.教师在教学中,应根据学生的学情,讲清数学概念、原理、方法、公式、定理,不是说只做基础不做难题,而是“磨刀不误砍柴功”.立足课本,夯实基础,怎么强调都不为过！

2.教师精心设计,引导学生回归概念,学会系统思维

经过分析可知,全国I卷函数与导数试题非常稳定,不偏不怪,重点内容重点考查.如2016年,2017年,2018年的全国I卷均考查了函数的零点和函数单调性问题,这两类问题都是一线老师熟悉的基本问题,我们很多学生花了大量的时间训练,效果即不尽如人意,原因何在?例如,有关函数的零点问题的试题层出不穷,解法千奇百怪.教学中,如果不加甄别全盘移植,教师只讲如何解题,不讲回归,学生只会程式操练,而不知函数零点的含义及其表征之间的联系,更不会建构研究处理函数零点问题的数学认知结构,那么就会阻碍学生的数学认知结构的发展,压缩学生的探究成长空间,教学效果大打折扣.

大道至简、平淡是真,我们的教学应回归基本概念,让学生学会系统思维.实际上,函数零点是中学数学的主体内容,是函数、方程、不等式的一个知识交汇点,比如,函数零点的含义与表征,函数零点的判定与求解,函数零点的分布与个数情况的讨论,函数零点在研究函数、方程、不等式中的应用等,都可以归结为函数零点问题.教学中如果教师能连点成线,由线到面,精心设计“问题串”[4],引导学生回归函数零点的概念展开系统研究,那么教学的效果就会大不一样了.

3.解题教学中,着重培养分析问题解决问题的能力

高考复习的教学主要是解题教学,树立正确的解题教学观很重要.解题教学的首要目的是巩固概念,最终目的是学会思考,过程中要培养良好的解题习惯、发展分析和解决问题的能力.通过“讲解题,不讲怎样解题”“讲解法,不讲如何想到解法”的方式给学生灌输技巧,最后总结为“解法—技巧”,这既加重学生的学习负担,又禁锢学生的思维,必须彻底纠正！[5]

“函数”始终贯穿高中数学,解题教学就要突出分析问题的过程,充分暴露思路探索过程,充分暴露遇到解题障碍的解决过程,引导学生对题目信息进行加工和挖掘,着重培养学生分析问题解决问题的能力.

4.学生跳出题海,老师跳进题海

要适应全国卷的命制方式,需要高中的数学教学与备考着眼于让学生“理解数学”,奢望让学生在题海中理解数学,它带来的后果必将是让学生只会依葫芦画瓢或生搬硬套.这种缺乏灵活性没有真正理解数学问题本质的备考在全国卷“基础中考理解”的模式下肯定难有成效.[6]题海战术出来的学生,解题“套路”意识很强,但是,不少试题你会发现“套路”“套”不进去,甚至走向了“不归路”.

学生跳出题海,做老师精选的试题,那么老师为了更好的选题,则应该跳进题海.给学生出一道题,老师可能要先做十道题,如果只是看而不做题,没有切身体验,很难使例题典型,讲解精彩,并会造成“该讲的讲不出,不该讲的拼命讲”.事实上,决定复习效果的关键因素不是题目的数量,而在于题目的质量和处理水平.一道好的题目,本身就蕴含了丰富的思想方法,经过适当变通、联想、拓展、延伸,以例及类,探求规律.老师就可以做到“讲一题,复习一片”的效果.

5.重视计算能力

这两年函数导数压轴题难度有所下降,但平均分仍然非常低,运算能力不足是一大原因.如2017年高考的函数导数大题第一问,大部分学生复合函数的导数求错,导致后面根本做不下去.

对于数学计算的问题,我们往往有一个误区,认为小学生才需要培养数学计算的能力,而高中生需要掌握的是宏观思考的能力,不再需要培养数学计算的能力.其实这是有失偏颇的,数学计算是数学知识的基础,只要学生学习数学知识,就必须强化数学计算的能力,尤其在全国卷的背景下,计算难度加大,一旦学生出现计算出错,后面的所有过程可能都是错的或者根本无法进行下去.

教师在平时的教学中,要多引导学生掌握一些常用的数学运算的技巧、方法和规则,可以精选一些计算量相对悬殊较大的题目,用充裕的时间去想去做,并结合这些实际题目适时灵活地运用概念、恰当地选择公式、合理地使用数学思想方法.从而达到简化计算、提高计算速度的目的.

6.加强学生自主探究能力的培养

在平时的教学中,老师包办读题过程和解答、学生重复模仿解题的做法比比皆是,学生失去了自主探究的机会,这样的结果就是,老师很累,效果却不理想.而且这种备考方法显然适应不了全国卷的以能力立意的命题特点.

教育家苏霍姆林斯基说过:“没有自我教育,就不是真正的教育.“饭是要亲自吃的”,教师应积极调动学生参与课堂,点燃学生主动思维的火花,给学生一定的探究平台、时间和空间,让学生在探究中发现错误,寻找错因,探究正解,在辨析中明理,在理解中内化,在纠错中升华.这样,比光听教师讲要深刻的多,效果要好的多.