基于改进粒子群的电水转换关系特征曲线研究
邬智俊,胡 钢,沈 波,刘美华,章梅娟
(1. 河海大学物联网工程学院,江苏 常州 213022;2. 南通市水利局,江苏 南通 226018;3.南通市供排水管理站,江苏 南通 226018)
“十三五”是全面建设成小康社会的关键期,也是加快转变水资源利用方式、提升国家水安全保障能力至关重要的五年。长期以来,农业灌溉用水占我国用水总量的比例最高,实际利用效率往往很低,造成了水资源的严重浪费[1,2],对农业用水进行计量收费是解决上述问题的有效途径。
目前,国内农业用水计量方式主要有直接计量和间接估算两大类,具体包括[3-5]:采用灌溉渠系上的水工建筑物测量;对于断面稳定没有回水影响的渠道内采用水尺观测;利用水堰、量水槽等特设量水设备进行测流;采用电磁流量计、超声波流量计等仪表设备进行计量;采用时间法、电水法、油耗法进行间接估算。
江苏某市农用电灌站数量庞大,水泵基本为中小型混流泵,这些泵站由于历史原因均未修建超声波流量检测围堰,且修建工作面临工程量大、经费需求高等难题,使得农业用水计量非常困难。综合该市实际情况和现有的农业用水计量方式,电水转换的间接测量方法更适合于该市农业灌溉用水的计量,其计量的精准程度与耗电量-供水量的关系特征曲线密切相关。
截至目前,针对排灌站中电水转换关系特征曲线的研究虽鲜有涉及,但电力系统和水土科学中的一些特征曲线的研究具有一定的参考价值。文献[6]采用遗传算法对火电机组的煤耗特性曲线进行拟合,反映了发电量和煤耗量间的关系;文献[7-10]阐述了层次贝叶斯算法、集合卡尔曼滤波算法、粒子群算法、萤火虫算法等改进的参数反演算法对于描述土壤水分特征曲线的VG模型参数优化,都具有很好的反演精度。鉴于此,本文重点研究了电水转换模型的构建,依次采用了最小二乘法(LSM)、粒子群算法(PSO)、改进粒子群算法(IPSO)分别对电水转换关系特征曲线参数进行优化,比较其拟合效果,选取适合的方法,为农业水量计量设备的研制提供理论基础。
1 电水转换模型构建
电水转换法主要通过自动化监测设备采集机泵的耗电量,依托耗电量-供水量转换关系特征曲线,间接计量泵站用水量。以往的工程中仅仅是把总供水量和总耗电量的比值视作电水转换经验系数,如式(1)所示。
TC=SW/SE
(1)
式中:TC为转换系数;SW、SE分别为总供水量和总耗电量。
式(1)理想化供水量和耗电量之间为线性关系且忽略了水泵期间的其他因素的影响,以此作为经验系数易造成较大的计量误差。
水泵在实际工作中的有效功率PE,实际消耗功率为PR。装置效率η为两者之间的比值,根据水泵的有效功率定义[11]和能量守恒定律可得:
PE=9.8FH=ηPR
(2)
式中:F为水泵的单位时间供水量,m3/s;H为水泵净扬程,m。
经过化简可得:
(3)
针对其他影响因素的问题,项目前期对江苏某市县下数多个镇上的几十座混流泵站进行了现场测试,得到如下结论[3]:①泵站的流量功率比不会随水泵规格的变化而变化;②在扬程变化不大的情况下,可忽略不计其对流量功率比的影响;③流量功率比和装置效率成正比关系。根据结论中②、③可得出:式(3)中的水泵净扬程H可视为定值;装置效率η在一个适当的功率区间(PRi,PRi+1)可认为不变。所以,电水转换关系特性曲线可以采用分段线性函数进行模拟,如式(4)所示。
(4)
PR区间的划分以及确定相应的η值是很困难的,并且分段线性函数较为繁琐,在微处理机上实现会增加其运算复杂性。鉴于此,对特征曲线进一步分析,在曲线上任意一点PR的瞬时变化率为:
(5)
式(5)反映了特征曲线的变化趋势,是一个递增函数;而装置效率取决于机泵效率、传动效率、管道效率、进出水池效率[12],其中机泵效率变动范围较大,电机空载时其效率和功率因数很低,随着负载增加而相应的增加,在额定负载下达到最大值。因此,整个特征曲线的变化趋势为递增,变化速率先缓后快。二次函数和三次函数均满足此种变化趋势,可以对式(4)进行简化,避免繁琐的问题,电水转化模型如下式所示,下文会针对这两种模型参数进行优化,选取性能最优的作为电水转换模型。
(6)
(7)
2 模型参数优化
一般的参数优化方法主要由待优化参数选取、目标函数的确定、参数样本空间生成和优化算法3部分组成。本文待优化参数为水电转化模型中的多项式系数,目标函数定义如下式所示。
(8)
式中:f*(xi)为拟合曲线上在x=xi对应的值;yi为样本空间中在x=xi所对应的实际值。
2.1 最小二乘法
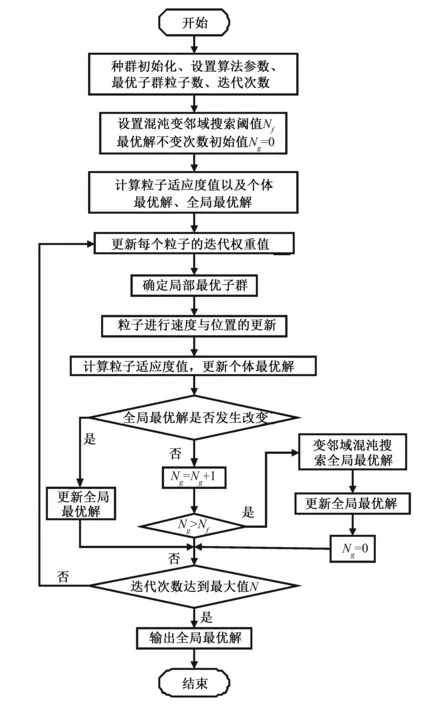
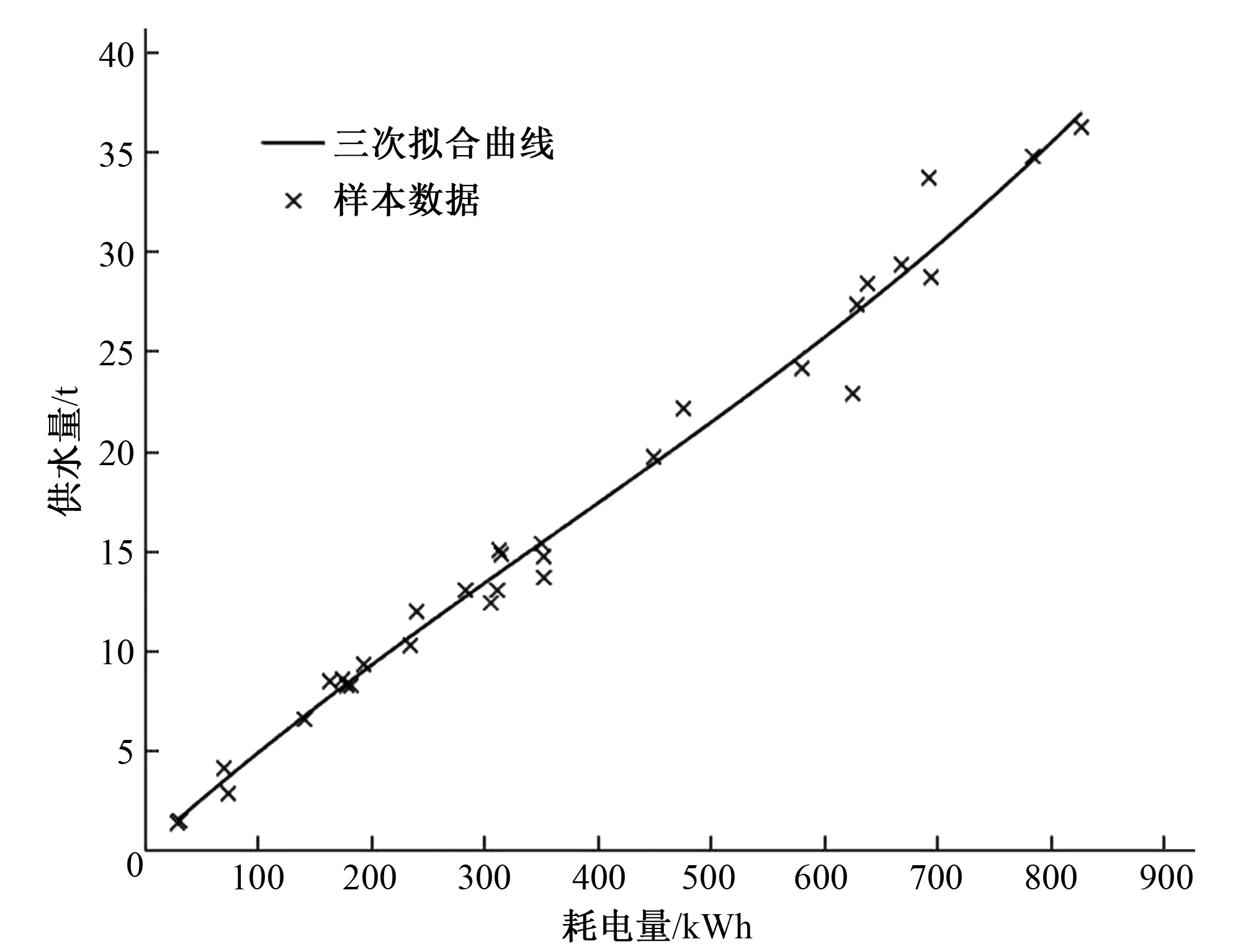
最小二乘法(LSM)作为一种数学优化方法,在曲线拟合中有着广泛的应用。给定一组散点(xi,yi)(i=0,1,,m)且a=x0 (9) 本文所需拟合的曲线为二次或三次曲线,为多项式拟合,则上述问题实际是求解U=U(a0,a1,a2,a3)的极值问题。由多元函数求极值的必要条件可知: 对式(10)进行化简,并整理成矩阵形式: 矩阵方程(11)的系数矩阵为4阶实对称矩阵,根据其性质可推出系数矩阵为正定矩阵,固矩阵方程存在唯一解。求解上述矩阵方程即可求出电水转换关系特征参数。 粒子群优化算法(PSO)是由James Kennedy和Russell Eberhart共同提出的,其本质上是一种多代理算法[13]。PSO基于鸟类觅食的基本思想(即一种信息共享机制,通过个体间的经验共享,以达到整个群体的发展和进化的目的),采用了“速度一位移”搜索模型。初始化时,每个粒子的位置和速度随机分布于解空间,然后根据个体最优极值和全局最优极值来动态调整自身的位置和速度,个体其迭代公式如下式所示。 (12) (13) PSO算法中需要调整的参数不多,实现简便,搜索速度快,但其具有陷入局部最优的问题。 2.3.1 自适应调整惯性权重 (14) (15) 初始阶段粒子迭代次数小、距离全局最优点远,速度更新步长大;后期变化规律相反,实现惯性权重的自适应调整。 2.3.2 变邻域混沌搜索 为了克服算法陷于局部最优解、求解精度不高的问题,在PSO中引入了变邻域混沌搜索,对算法的性能进行了优化。当全局最优解在一定次数内不再更新的时候,便开始变邻域混沌搜索,即改变寻求最优解的邻域范围,若全局最优解不再改变,说明上次的结果为全局最优解,否则更新全局最优解。变邻域混沌搜索实质上是一种全局最优解的变异过程,以增加获得最优解的可能。变邻域混沌搜索全局最优解具体步骤如下。 (1)利用logistic函数产生一个混沌变量: Ui+1,j=4Ui,j(1-Ui,j) (16) 式中:Ui,j为初始混沌变量值,在(0, 1)之间,且不等于0.25、0.5、0.75;Ui+1,j为下一代混沌变量值。 (2)将产生的混沌变量映射为变量变化值: Δxi=-β+2βUi+1,j (17) (18) 式中:β为邻域半径;Δxi为个体最优解或者全局最优解的位置偏移;xmax、xmin为粒子位置的最大和最小值;tmax为最大迭代次数。 (19) (4)更新全局最优值。 (20) 改进粒子群优化算法的流程图如图1所示。 图1 改进粒子群算法流程图 实验数据来源于江苏某市下的电灌站,该泵站装有电表、流量计,在农田灌溉期进行长期实验,获取耗电量和供水量的数据集。分别采用LSM、PSO和IPSO这3种算法进行优化拟合,分析其算法性能。实验数据共31组,粒子群算法的参数设置如下:粒子种群个数N=40;学习因子c1=c2=1.495 5;惯性权重ω=0.729 8;搜索空间维数为求解参数个数;最大迭代次数Iteration=500。表1和表2为LSM、PSO、IPSO算法对于不同阶数特征参数优化结果比较;图2为PSO和IPSO算法性能比较。 表1 不同算法电水转换二次特征曲线参数求解 表2 不同算法电水转换三次特征曲线参数求解 图2 算法性能比较图 比较表1和表2中3种算法优化拟合到的多项式系数,参数计算偏差值不是很大,但适应度值即最优化准则函数值IPSO明显优于PSO和LSM,表明IPSO具有很好的寻优精度。由图2可知,由于IPSO能够进行惯性权重的自适应调整和进行变邻域的混沌搜索,相比于PSO能够快速寻优,有更好的收敛速度。采用改进粒子群算法(IPSO)计算电水转换参数,绘制电水转换关系特征曲线,如图3和图4所示。由图3和图4显示,两种曲线都能很好地拟合出供水量随耗电量的变化趋势,数据点都能紧密的分布在曲线附近,结合表1和表2可知,采用三次函数拟合电水转换关系特征曲线的适应度值(残差平方和)明显小于二次函数拟合效果,表明式(7)更适合作为电水转换模型。 图3 IPSO拟合电水转换关系二次特征曲线 图4 IPSO拟合电水转换关系三次特征曲线 本文首先研究了电水转换模型,对传统的电水转换模型进行了优化改进;其次针对粒子群算法的缺陷,提出了基于自适应调整惯性权重和变邻域混沌搜索的改进粒子群算法;最后采用LSM、PSO、IPSO对模型参数进行寻优,仿真结果表明3种算法都适用于模型参数拟合,IPSO寻优精度更高、有更好的收敛速度,拟合的特征关系曲线能够更真实的反应耗电量和供水量的关系,为农业用水计量设备的研制提供理论基础。2.2 粒子群算法

2.3 改进粒子群算法


3 算例分析




4 结 语

