含弹内埋弹舱缩尺模型气动噪声特性研究

刘兴强，黄文超，郭定文，延浩，宁方立

（1.中国飞机强度研究所，西安 710065；2.西北工业大学，西安 710072）

现代先进战斗机和远程轰炸机多采用的内埋武器弹舱，在空中打开时，由于高速气流与空腔结构的耦合，在舱内及周边产生强烈的噪声环境。空腔的低频高声强纯音噪声通常具有很高的声能量，低阶频率往往在结构的谐振频率范围内，极易导致结构共振。从而，在短时间内使内埋弹舱及周边飞机结构发生声疲劳破坏。

从20世纪50年代起，国外研究人员就开展了空腔流动与噪声特性相关问题研究。Rockwell与Naudascher将空腔的流动分为流腔耦合机制、流声共鸣机制、流固耦合机制三种流动状态[1-3]。Sarohia、Plentovich、Dix等多位研究者根据空腔不同长深比对流场特性影响，提出了不同的空腔分类[4-7]。Plentovich采用试验方法研究了来流马赫数和雷诺数对空腔噪声的影响，指出空腔的分类不仅依赖于空腔尺寸，也依赖于来流速度[5]。Rossiter提出了空腔纯音噪声的预计经验公式[7]，Heller[8-9]将 Rossiter经验公式进行了改进。Shaw[10]对F-111弹舱噪声问题进行了试验研究，试验室得到了与Rossiter频率相吻合的峰值噪声，但飞行测试得到的峰值频率与 Rossiter频率差别较大。McGrath[11]等人研究了空腔噪声的主被动控制方法，得到较好的降噪效果。由于计算方法和计算机技术的进步，采用数值方法对空腔的流动和噪声问题进行分析成为一个有效的途径。Colonius[12]采用 DNS研究了两种结构外形的空腔的流场特性，成功捕捉了空腔内的剪切层模态和尾迹模态。Shieh与Morris[13-14]采用DES湍流模型，基于高阶差分DRP空间离散格式，研究了二维空腔流动和声场特性，得到了与Rossiter相吻合的纯音噪声。Stanek[15]采用LES研究了内埋武器弹舱的流动特性。国内的研究相对较晚，李晓东[16]、罗柏华[17]、杨党国[18]等人对空腔的流动和噪声特性也开展了大量的研究。文中针对含弹内埋弹舱缩比简化模型的空腔噪声进行了数值计算，并且在声学风洞中进行了吹风对比试验。通过研究获得了一些有价值的数据，可以为内埋弹舱的设计提供参考和技术支持。

1 空腔噪声计算方法

文中采用“CFD+CAA”的混合计算方法计算内埋武器弹舱空腔噪声。非定常流场计算采用DDES，获得空腔内的非定常流场信息。声场计算采用Möhring声学类比方法。Möhring声学类比方法是 Lighthilll修正，根据Lighthill声学类比方程，考虑到流场中的非等熵效应及非均匀流对声波传播的影响，对 Lighthill声学类比方程进行修正，得到：

式（1）左侧为声传播算子，右侧R为声源项，忽略黏性的影响，声源项只和Lamb矢量的散度相关。将Möhring声类比与Curle积分相结合，声源项可以写成如下形式：

声源项式(3)第一项为空间四极子噪声，第二项为物体表面的偶极子噪声，计算更加接近真实情况，结果更加准确。近场声传播计算基于声学有限元，远场声传播计算基于声学无限元方法。为了减少声场计算信号的渗漏误差，计算中添加了Hanning窗。

2 标准算例验证

首先通过对比算例验证本文算法，为此采用M219空腔标模，这是美国在研究内埋武器弹舱流动时采用的标准模型。该模型在QinetiQ风洞中进行了一系列的试验，相应的试验数据被用作研究内埋武器弹舱的流动和噪声研究的基准。空腔结构尺寸：长度为0.508 m，深度0.1016 m，宽度0.1016 m，长深比（L/D）为5，空腔底部沿流向均匀地布置10个声压测量点。

计算采用理想气体，来流温度为266.5 K，来流速度为 0.85 Ma，基于空腔长度的雷诺数为 7×106。计算得到的空腔底部某测量点处的噪声频谱曲线如图1所示，空腔的第一阶峰值频率为145 Hz，第二阶纯音峰值频率为 379 Hz，第三阶纯音噪声的频率为584 Hz。该测量点处纯音噪声计算与试验、经验公式的对比见表1，可以看出，纯音的频率与幅值与试验吻合很好，表明文中采用的算法可以准确地预测空腔的峰值噪声。

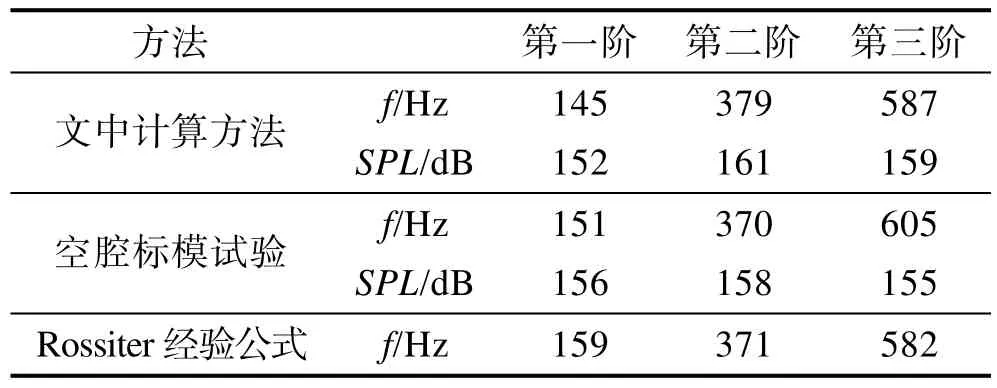
表1 测量点4噪声与试验对比

3 含弹内埋弹舱模型

含弹内埋弹舱的模型如图2所示，弹舱内含有两个弹体。弹舱长为430 mm；深为60 mm；宽为64 mm，是某型弹舱的 1/10缩比模型。弹舱的场深比L/D=7.17，是典型的开式空腔。腔内的共安装了 18个噪声测量点。其中，底部7个，侧面9个，后壁2个，具体位置如图3所示。

4 含弹内埋弹舱噪声计算

流场计算采用结构网格，网格量为2200万，空腔腔体周围物面的网格如图 4所示。计算主要针对0.45，0.7 Ma两种工况状态。气体为理想气体，温度为263 K。

图5 a为定常流场计算0.45 Ma弹舱中间截面的速度分布云图，外部的高速气流与腔内的低速气流之间形成强烈的剪切层，剪切层横跨弹舱对空腔后壁产生强烈的冲击。图5b为0.45 Ma中间截面的涡量分布云图，气流在弹舱的唇口处形成了强烈的涡，随气流传播，对后壁冲击产生强烈的噪声。

5 内埋弹舱噪声试验

5.1 试验设置

内埋弹舱噪声试验在中国飞机强度研究所航空噪声与动强度航空科技重点实验室的全消声室中进行。全消声室容积为144 m3，长6 m，宽4 m，高6 m，有效噪声测量频率为50 Hz～20 kHz。试验现场布置如6图所示，来流速度分别为0.45，0.7 Ma。

试验与计算的弹舱内部测量点保持一致，噪声测量点采用的是高声强传声器B&K4938和B&K4136，声学信息采集装置采用B&K3660D，相关的设备参数见表2。

表2 试验设备参数表

5.2 噪声源识别结果

试验采用传声器阵列对弹舱的主要噪声源的位置进行识别。阵列采用螺旋阵，口径为0.8 m，24个通道，测量传声的动态范围20 Hz～16 kHz，阵列测量中心距弹舱 1.55 m。阵列的后处理采用 CLEAN-SC算法。图7a和b分别显示了0.45 Ma和0.7 Ma状态下内埋弹舱主要噪声源的位置。其中，0.45 Ma下中间弹翼处的噪声最为严重，而0.7 Ma下主要噪声源在中间弹翼偏下游的位置。

6 计算与试验的结果对比

空腔底部6号测量点处，在不同来流速度下，计算得到的频谱与试验结果的对比曲线如图8所示，计算值与试验值的宽频噪声基本吻合。纯音频率的对比见表3，0.45 Ma时，计算得到的高声强纯音频率与经验公式基本一致；0.7 Ma时，计算得到的纯音噪声较经验公式偏低。

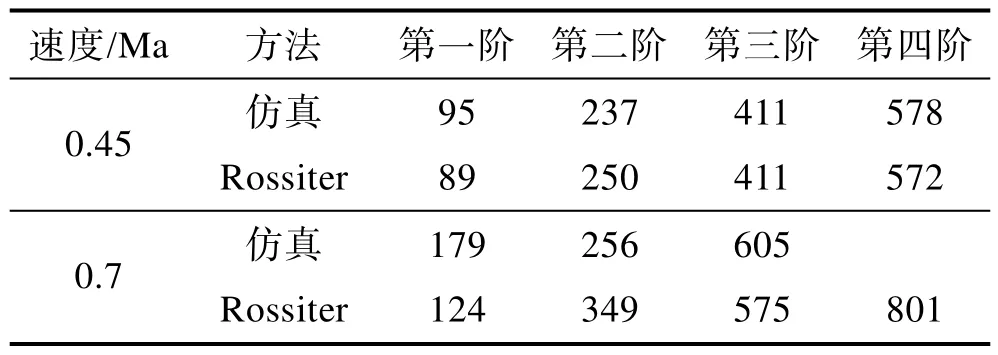
表3 仿真与试验纯音频率对比

计算得到的弹舱内部测量点总声压级曲线如图9所示，可以看出，弹舱下游的噪声比上游强烈。0.45 Ma时最高声压级出现在中间弹翼附近的侧壁15号测量点；0.7 Ma时最高声压级在空腔后部上游弹翼和下游弹翼之间的侧壁17号测量点。这与声源识别得到的主要噪声源的位置基本一致。

7 结论

针对内埋弹舱含弹情形下的噪声进行了仿真计算与试验研究，并将仿真与试验得到的噪声频谱曲线进行了对比，得到如下结论。

1）文中计算方法针对标准空腔模型M219得到的纯音噪声的频率与试验及 Rossiter经验公式基本一致。

2）0.45 Ma与0.7 Ma含弹的情况下，底部测点的试验与仿真得到的噪声结果宽频十分吻合。

3）仿真得到的纯音噪声频率与 Rossiter频率比较接近。

4）弹舱内下游的噪声高于上游噪声，中间弹翼附近的噪声最为强烈。

5）随着气流速度增大，最强噪声向空腔后部移动。