基于经验模态分解与小波分析的超声信号降噪方法*

刘 备， 董 胡， 钱盛友

(湖南师范大学 物理与电子科学学院， 湖南 长沙 410081)

0 引 言

经验模态分解对数据有着良好的自适应性， 能够对非线性、 非平稳性信号进行线性化和平稳化处理， 并在分解的过程中保留数据的本身的特性， EMD方法无须预先设定任何基函数， 这一点与建立在先验性小波基函数上的小波分解方法有本质的区别. 利用EMD的分解， 将信号从高频到低频依次分解得到多级IMF分量， 选择性地选取需要的IMF分量并对其进行信号重构， 从而得到去噪后的信号. 如今国内外专家已将其应用于各种信号噪声压制， 例如地震噪声压制、 煤岩冲击破坏信号去噪、 机械故障诊断等领域[1-6]， 取得了较好的应用效果. 但是在实际应用中发现， 在处理与噪声时频特征相近的信号时， EMD分解存在模态混叠的现象， 即有些IMF分量仍然是信号与噪声共存. 虽然后续又提出了改进版本的总体平均经验模态分解(Ensemble Empirical Mode Decomposition， EEMD )[3]， 杨辉等人也提出了经验模态分解与小波相结合(EMD-小波)的去噪方法[5]， 即直接剔除代表高频噪声的imf1分量， 对其余的IMF分量采用小波去噪之后再累加重构得到去噪后的信号， 但仍然无法消除信号与噪声模态混叠的问题. 为了解决EMD去噪中模态混叠的问题， 提高超声信号的去噪效果， 本文提出了一种基于经验模态分解与小波分析的去噪方法， 旨在达到更好的信号去噪效果.

1 算法原理

1.1 经验模态分解

EMD能将信号自适应地分解成不同时间尺度的IMF分量， 分解得到的IMF分量必须满足两个条件[6]： ① IMF中极值点的个数与过零点的个数相等或不超过1个； ② 由极大值与极小值确定的包络线均值为零； 设信号为x(t)， 则EMD分解成一系列的IMF分量后可表示为

(1)

式中：imfi(t)为第i个IMF分量；r(t)为分解残余项. 分解得到的IMF分量按高频到低频顺序排列， 将EMD方法应用至信号降噪中， 通常把高频的IMF分量作为噪声剔除， 对余下的IMF分量进行重构， 即可实现去噪. 但由于IMF中存在信号与噪声模态混叠现象， 简单重构IMF分量可能导致去噪效果不佳[1].

1.2 互相关系数

对含噪信号进行EMD分解得到多个IMF分量; 然后计算得到各IMF分量与噪声信号的互相关系数， 式(2)是本文的互相关系数定义.

(2)

1.3 小波去噪

小波变换实际上是对函数的分解， 小波变换具有带通的功能， 即可以利用小波变换将原信号分解成不同频率的信号， 每个频率带互不重叠， 所分解的频率区间包含了原函数的所有频段. 由于信号中的有用部分与噪声具有不同的时频特性， 进而小波去噪主要包括以下3个基本步骤:

1) 选择合适的小波基函数及其分解层次， 同时计算每层小波的分解系数；

2) 针对每一分解层次选择一个阈值对高频系数进行处理， 去除集中在高频部分的噪声成分；

3) 针对每个分解层次， 对低频系数和阈值量化处理后的高频系数进行小波重构， 获得去噪后的信号.

选择不同的小波函数及其不同分解尺度对加噪后bumps信号进行去噪， 采用式(3)的信噪比SNR对去噪效果进行定量分析， 信噪比SNR的计算表达式为

(3)

(4)

则降噪之后的信号与原始信号的相对能量比公式可定义为

(5)

式中：E表示原始信号能量；E0为去噪后信号能量.

2 实验方法与结果

2.1 加噪信号去噪

以加入5 dB的高斯白噪声的bumps信号(信号长度为1 024)EMD去噪为例， 加入噪声前后的bumps信号波形及其频谱如图 1 所示. 采样频率为100 Hz， 对图1(b)中的加噪bumps信号进行EMD分解， 得到的前8个IMF分量如图 2 所示.

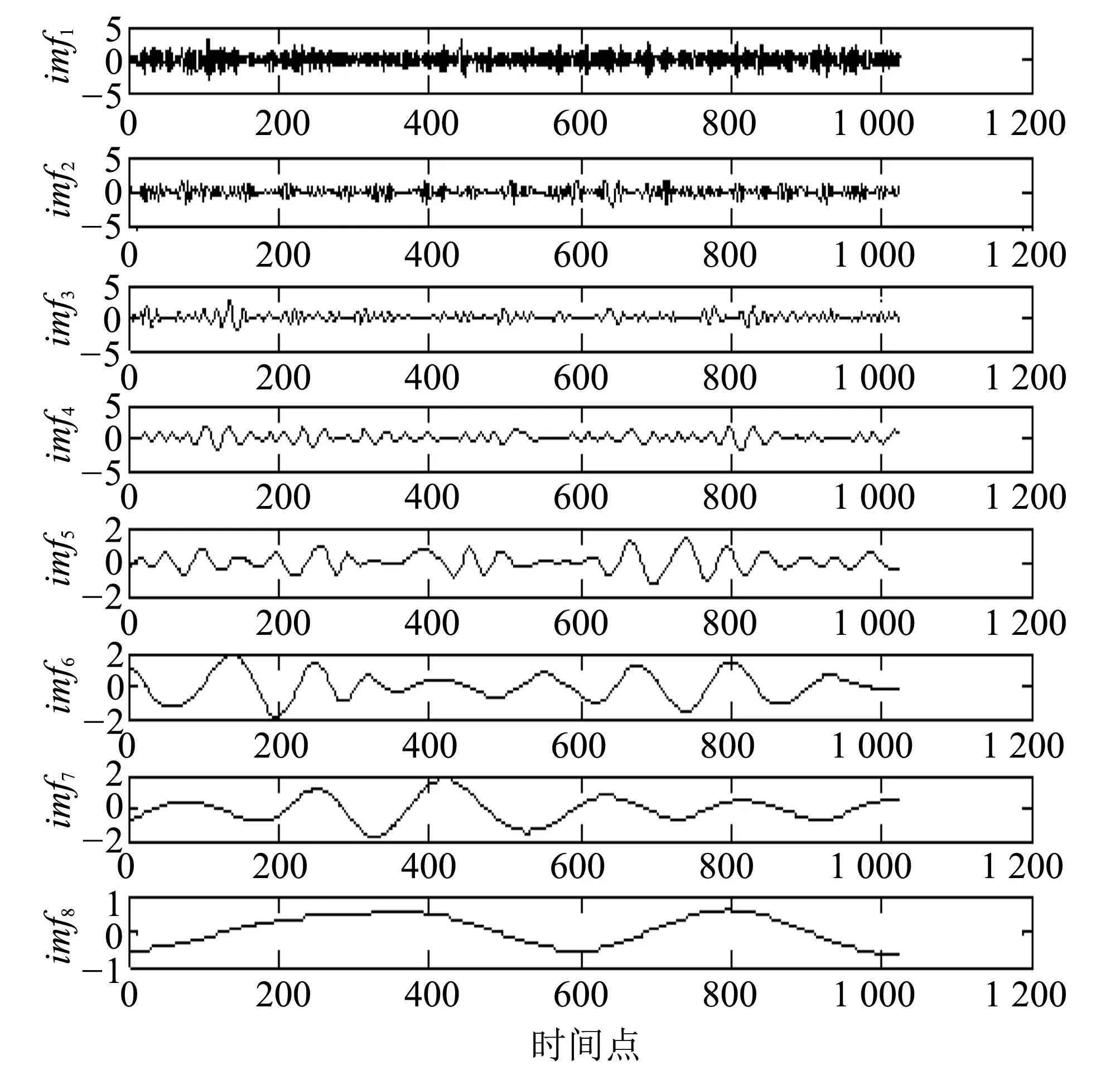
图 2 经验模态分解结果Fig.2 Empirical mode decomposition results

根据式(2)， 计算图1(b)中加噪bumps信号经EMD分解后的各IMF分量与加噪信号之间的互相关系数， 计算结果见表 1.

表 1 各IMF分量与bumps含噪信号的互相关系数

表 2 不同去噪方法效果比较

图 3 小波去噪前后过渡分量imf3和及频谱Fig.3 Transition component imf3 and and their frequency spectrum before and after wavelet denoising

图 4 本文方法去噪后波形与其频谱图Fig.4 The denoised signal waveform and its spectrum in this paper

2.2 实际超声信号的去噪结果

1 MHz的超声信号透过生物媒介后的波形及其频谱如图 5 所示， 明显可见： 透过生物媒介接收到的超声信号的主频主要分布在1MHz左右， 但含有较多高频噪声， 因此要对含噪信号做去噪预处理.

图 5 实际超声信号及其频谱Fig.5 Actual ultrasonic signal and its spectrum

生物组织透射法接收的超声信号经过EMD方法分解后可以得到按高频至低频的多个IMF分量， 这些IMF分量的主频表现得比较集中， 这对模态混叠的IMF分量进行小波去噪滤除噪声是比较有利的. 利用EMD的这项优势， 使本文提出的EMD去噪方法适用于处理超声信号. 根据1.2节中所述方法， 通过计算EMD分解得到的各IMF与超声信号之间的互相关系数， 选取imf4作为过渡分量， 并对其做小波去噪， 过渡分量imf4去噪前后波形及频谱如图 6 所示. 利用所述方法对实际超声信号进行去噪， 去噪后信号及其频谱如图 7 所示. 分析图 7 发现： 去噪后信号接近主频为1 MHz的正弦波， 利用本文去噪方法， 可有效降低模态混叠分量的影响， 提升超声信号的去噪效果， 为HIFU治疗的疗效评价提供洁净信号支持. 由于实验采集的超声信号， 其对应的真实信号很难获得， 因此采取去噪后信号相对于频率为1 MHz 的超声正弦波信号的互相关系数来评价去噪效果. 互相关系数越小去噪效果越好， 反之则差. 本文方法去噪后信号相对于上述正弦波信号的互相关系数高达0.98， 且信号幅值没有失真.

图 6 小波去噪前后的过渡分量imf4与及其频谱Fig.6 Transition component imf4 and and their frequency spectrum before and after wavelet denoising

图 7 本文方法去噪后波形及频谱Fig.7 The denoised signal waveform and its spectrum in this paper

3 结 论

本文在经验模态分解的基础上， 通过观察各模态分量与原信号间的互相关系数的变化， 可以有效识别出存在一定模态混叠问题的过渡分量(含有噪声和有用信号)， 在一定程度上有效去除了过渡分量中包含的噪声成分， 为之后的信号重构提供相对纯净的信号分量. 以加噪信号和实际超声信号的去噪为例， 对比不同方法去噪之后的信号波形以及频谱分析， 定性说明了本文方法的可行性； 通过对比各种方法去噪之后的参数指标， 定量证明了本文方法的合理性和有效性. 互相关系数在EMD去噪中的应用进一步改进了EMD去噪方法， 能较好地处理信号模态混叠噪声， 可尝试将本文方法应用于其它类信号去噪， 具有较为广阔的应用前景.