漆膜制备机器人喷枪轨迹生成与优化研究综述*
刘仲义,吴清锋,王海霞,王清忠,陈丛亮
(1.广东产品质量监督检验研究院国家工业机器人质量监督检验中心,广东佛山 528300;2.广东工业大学机电工程学院,广东广州 510006)
0 引言
漆膜制备是涂料检测的关键一环,漆膜的质量的好坏很大程度上决定了涂料检测过程中的性能的优劣。目前,涂料检验室检测中的漆膜制备大多数由人工完成,但是人工喷涂效率低、质量差、环境恶劣,且喷涂过程中的噪声和飞溅的溶剂都会对人体造成伤害。工业机器人的出现解决了这一难题,经过几十年的发展,工业机器人已被广泛应用于汽车、家具、船舶、航天等行业的喷涂作业中。机器人喷涂具有涂层质量好、工作效率高、油漆耗量低、适用范围广等优点。
涂料检测中,对漆膜的质量有着严格的要求,而漆膜的质量由很多因素决定,如喷涂距离、喷枪的流量、涂料粘度、喷枪的运行速度、工件表面的温度分布、漆膜的均匀性等。其中,漆膜厚度的均匀性是决定性因素,均匀的漆膜厚度可以降低工件表面的涂料用量,节约喷涂成本,减轻涂料对环境的污染;漆膜厚度不均匀会导致涂料桔皮和边缘涂料流挂,且漆膜过厚还会导致漆膜胀裂。影响漆膜厚度均匀性的因素主要包括涂料的选取、喷枪轨迹、喷涂速度的平稳性、喷涂方向等,关键因素是喷枪的轨迹规划。因此,在涂料的选用已经确定的情况下,研究喷枪轨迹的生成和优化对保证漆膜质量具有重大的意义。
喷涂机器人喷枪轨迹的生成与优化是喷涂机器人离线编程中的关键技术,国内外许多专家学者对其展开了深入的研究[1-2]。A.Klein[3]提出了一种基于CAD模型的喷涂机器人离线编程系统,通过该系统可对喷枪的运动轨迹进行设计和仿真。Antonio等[4]提出了针对规则平面的喷枪模型,以被喷涂表面上任意一点的实际漆膜厚度和工件表面理想漆膜厚度之间的最小方差为目标函数,总结了喷涂轨迹、喷枪速度、喷枪走向、喷涂张角等因素对漆膜质量的影响。Balkan等[5]经过大量的实验得到了漆膜厚度β分布模型,建立了针对平面的喷枪轨迹优化方法,并通过实验加以验证。Hansbo等[6]提出了一种简单的数学模型来模拟不同喷射距离和方向时的涂层厚度,同时也提出了一种迭代法对喷涂机器人的运动轨迹进行了优化,并通过实验加以验证。Zaki等[7]利用两台离线CCD摄像机得到物体表面CAD模型,并对喷涂机器人喷枪的三维空间轨迹进行了求解。W.Sheng等[8]根据待喷涂工件的表面形状,创建了喷涂机器人喷枪路径生成的相关规则,且提出影响喷枪空间路径生成的主要因素是两个喷涂轨迹间的间距。Chen等[9]结合自由曲面CAD模型和喷枪模型,研究了自由曲面上喷枪轨迹自动生成方法,该方法能有效满足所需的涂层厚度。
1 涂料沉积模型
涂层的累积速率决定了漆膜的厚度分布,即涂层的均匀性。因此,首先要建立涂料沉积模型[10]。目前,常用的获取涂层沉积模型的方法有两种,第一种是采用现有的一些数学模型,如无限范围模型(柯西分布模型[11]、高斯分布模型[12])和有限范围模型(椭圆形分布模型、抛物线分布模型、β分布模型、椭圆双β分布模型[13]、分析沉积模型、组合模型)。这种方法建立的数学模型中的函数相对平滑,但是表达式相对复杂,主要适用于平面和规则曲面的喷涂。第二种是通过经验或者实验获取涂层厚度数据,推导出涂层累积速率模型。这种方法是根据离散的数据创建的数学模型,其函数更接近实际的喷涂作业,适合应用于一些复杂的自由曲面的喷涂。
1.1 适用于平面和规则曲面喷涂的涂料沉积模型
1.1.1 β分布模型
通过分析实验数据得到的β分布模型是一种较好的漆膜厚度分布模型,它有一个可供选择的造型参数β,当β取不同值时,对应的漆膜厚度分布模型也不一样。假设喷枪的喷涂空间为圆锥形,如图1所示,则漆膜累积速率可表示为[14]:
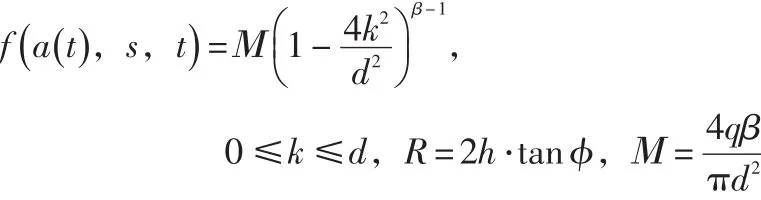

图1 β分布模型Fig.1βdistribution model
式中:d为喷涂空间直径;k为喷涂空间内一点到喷涂中心的距离;h为喷枪到工件表面的垂直距离;ϕ为喷涂圆锥张角的1/2;M为最大喷涂厚度;q为涂料流量速率。1.1.2高斯分布模型
假设把粉末颗粒在工件表面的沉积当作一个概率性事件,则可采用高斯分布来进行说明,由经验公式推算出来的高斯模型,更接近实际的喷涂作业。通过调整模型的参数可以对最大喷涂量、喷涂空间、喷涂均匀性进行控制。如图2所示[15],高斯函数模型可以表示为:

式中:Qmax表示漆膜的最大厚度,δx表示沿着x轴方向的高斯参数,δy表示沿着y轴方向的高斯参数。
1.1.3 椭圆双β分布模型
椭圆双β分布模型在平面的喷辐为椭圆形,如图3所示[16],更加符合实际的喷辐形状。当喷枪的轴线垂直于待喷涂平面进行喷涂时,平面上漆膜厚度累积速率可以表示为[13-16]:

式中:q(x ,y)表示工件表面一点的漆膜厚度累积速率函数;du表示单位时间内喷涂中心的漆膜厚度;m为椭圆的长轴,n为椭圆的短轴; β1、 β2为形状参数。

图2 高斯分布模型Fig.2 Gaussian coating thickness
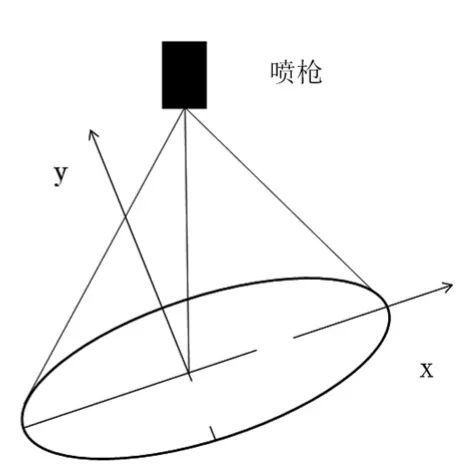
图3 椭圆双β分布模型Fig.3 Elliptical double βdistri⁃bution model
1.2 适用于复杂自由曲面的涂料沉积模型
喷枪的位置和姿态在固定的笛卡尔坐标系OXYZ中可定义为一个六维的时间的矢量函数:a(t)=[p (t),o(t)]T,其中p(t)=[px(t),py(t),pz(t)]T,表示喷枪相对于坐标系OXYZ的位置;o(t)=[ox(t),oy(t),oz(t)]T,表示喷枪相对于XYZ轴的旋转角度。
假设喷枪的喷涂空间是一个锥体,那么涂料在待喷涂平面的空间分布模型如图4所示。图中h表示喷枪与平面的距离,ϕ是圆锥的张角,R是平面上的喷涂半径,r是平面上一点s到喷涂中心的距离, θ是点s和喷枪的连线与喷枪中轴线的夹角。由此,平面上的漆膜累积速率G可以表示为:G=f(r,h)。实际喷涂过程中,喷枪离待喷涂表面的距离一般都保持不变,则漆膜累积速率只与r相关:G=f(r)。此时漆膜累积速率G与r的函数图形可以近似看成是一个二次曲线[17],如图2所示。所以,通过Goodman的方法测得的平面上不同位置的漆膜累积速率数据[18],就能得到G的函数表达式。

图4 涂层空间分布模型和涂层累积速率函数图Fig.4 Coating space distribution model and coating accu⁃mulation ratefunction

图5 自由曲面上的涂层累积模型Fig.5 Coatinggrowth model on freeformsurface
图5 为复杂表面上的涂料累积模型。P1是建立的参考平面,P2过点s并跟P1平行,θi为喷枪和点s的连线与喷枪中心线的夹角,h和hi分别是喷枪到平面P1、P2的距离。设P1和P2上的涂料量是一样的,喷枪在P1上的喷涂区域为c1,c2是喷枪在P2上的喷涂区域,则c1和c2的面积有以下关系:
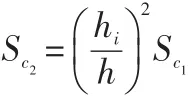
设c1上的漆膜厚度为q1,则c2上的漆膜厚度q2可以表示为:
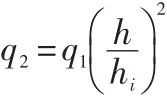
假设c3与喷涂方向垂直并跟c2处在相同的喷涂情况下,如图6所示,c3与c2的夹角为θi;设c4为过点s的圆形面,c3的法向量和c4的法向量夹角为γi,如图6所示,则c3和c4上的漆膜厚度分别为:


自由曲面上的漆膜厚度可以表示为[19]:
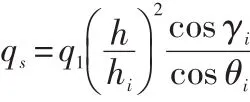
假设曲面上一点s到喷枪中心的距离为li,则有hi=licosθi。在进行喷涂时,如果γi≥90°,则该区域为喷枪的喷涂死角。所以自由曲面上一点s的漆膜厚度可以表示为[19-20]:


图6 不同夹角圆形面之间关系Fig.6 Relationship between round surfaceswith different angles
2 工件表面造型方法
喷涂工件表面造型是喷枪路径生成的前提,也是喷枪轨迹优化的关键。因为实际待喷涂工件曲面的复杂多样,目前为止还没有一套通用的工件表面造型方法。为了更好地对喷涂机器人的喷涂轨迹进行优化,采用一种合适的工件表面造型方法是非常重要的。在喷涂机器人的轨迹规划中,主要有三类工件表面造型方法。
2.1 基于参数曲面的工件造型方法
计算机辅助几何设计(CAGD)有多种造型方法,如Bezier法、B样条法、非均匀有理B样条法(NURBS法)等;以上方法都是在逼近的基础上,通过操纵多面形产生曲线或曲面,这样就可以减少设计难度。该造型方法主要有两个步骤:(1)求得逼近于待喷涂曲面的参数曲面的数学公式;(2)找到该参数曲面的等距面,以便从等距面上对喷涂路径进行规划。该造型方法有两个关键因素:(1)表示参数曲面的几何代数公式的复杂程度(代表着参数曲面逼近的精度)[20];(2)等距面与参数曲面的距离大小(影响着漆膜质量)。随着现代工业制造技术的持续发展,实际喷涂作业中的待喷涂表面形状愈加复杂,大部分为自由曲面。如果采用该方法对工件进行造型,那么得到的参数曲面数学表达式将会非常复杂,从而增加喷涂轨迹优化的难度。
2.2 基于模型的工件造型方法
该方法是先通过其他方式来得到待喷涂工件的CAD模型数据,然后通过CAD数据对喷涂路径进行规划。目前使用比较广泛的有两种:(1)空间模型转换法,其步骤为:先把待喷涂工件转变为CAD模型,然后通过CAD模型对喷涂机器人的喷涂路径进行规划,最后把规划完成的喷涂路径转变到三维空间中去。(2)三角网格划分法,其步骤为:首先通过工件的CAD模型来对工件表面进行三角网格划分,然后利用划分好的三角网格曲面对待喷涂工件表面进行逼近。以上方法对一些要进行分片处理的复杂形状工件并不适用,在完成造型后,如何将每个分片上喷涂轨迹进行整合是个难题。
2.3 基于扫描系统的工件造型方法
假如缺少工件的模型数据,或当待喷涂工件表面形状和工件模型的数据不吻合时,那么就需要对工件进行扫描,得到正确的工件模型数据。该方法的步骤为:首先通过扫描系统扫描工件,得到工件表面的模型数据,然后利用相应的参数曲面对工件表面进行逼近,最后对喷枪的喷涂路径进行规划。该方法对一些具有复杂曲面且需要进行分片处理的工件并不适用。
3 优化目标
在喷涂机器人轨迹优化过程中,主要有两个优化目标:第一是满足涂层厚度要求的前提下,尽量使漆膜厚度均匀,即漆膜厚度变化最小;第二是在满足涂层厚度要求的前提下,使喷涂的时间最短。目前研究最多的是第一种情况,求涂层厚度变化最小。因为工件的待喷涂表面任何一点的实际漆膜厚度与整个工件表面上的平均漆膜厚度之间的差值可能为负数,所以差值之间有可能相互抵消。为了防止这种情况的发生,选用工件待喷涂表面上实际涂层厚度与整个工件表面的平均涂层厚度之间的方差最小作为优化目标[21]。

As为待喷涂表面的面积,则漆膜厚度变化方差函数Vs(a (t))为:

4 喷枪轨迹优化
目前喷枪轨迹优化主要有两种情况。第一种情况是已知喷涂机器人的喷涂路径,然后再让喷枪沿着路径喷涂,这时候,喷涂轨迹的优化目标就变成了怎样得到喷枪沿指定路径喷涂的最优时间序列[2,19],即喷枪以何种速度沿指定路径喷涂时,漆膜厚度最均匀。第二种情况是喷涂机器人的喷涂路径是未知的,喷枪的喷涂轨迹是以时间为变量的六维矢量的集合,因此这种情况比较一般,求解过程更为复杂。
4.1 沿指定空间路径的喷枪轨迹优化问题
此种情况下已知喷枪的空间位置和姿态,定义六维时间矢量a(t)来表示,设喷枪的空间路径为六维矢量函数Ρ(ρ),标量 ρ∈[0 , 1], Ρ(ρ)是参数 ρ的连续函数。定义时间标量函数 λ(t ), λ:[0 , T ]→ ρ∈[0 , 1],把参数 ρ转换成标量函数λ(t),那么矢量函数Ρ(λ (t))也表示空间路径Ρ(ρ)上所有点的集合。为了使喷枪运动轨迹光滑,设λ(t)为连续函数,通过限制λ(t)的一阶、二阶导数的值来控制喷枪的速度和加速度;为了使问题更为简单,设λ(t)为单调递增函数,用标量函数集合Λ(t)表示最终的λ(t),所以,沿已知路径Ρ(ρ)的喷枪轨迹优化问题可以表示为:
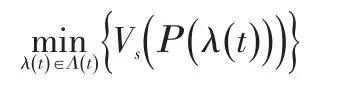
4.2 一般约束条件下的喷枪轨迹优化
一般约束条件下,喷枪的空间位置和姿态是未知的,直 接 定 义 六 维 矢 量 Ρ(t)∈R6,代表时间变量,Ρ(t)代表喷枪在空间中的一条轨迹,设Α(t)为可选的喷枪空间轨迹(六维)的集合[2],则一般约束条件下的喷枪轨迹优化问题可以表示为:
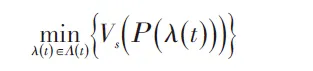
5 结束语
漆膜制备机器人喷枪轨迹生成与优化对漆膜的质量具有重要意义,国内外许多专家学者已对其进行了大量的研究和试验,有了许多的理论和成果,针对平面和规则曲面的喷枪轨迹生成与优化已经成熟,但针对复杂曲面的喷枪轨迹的生成与优化还不完善。随着现代工业的发展,被喷涂工件的表面形状越加复杂,人们对漆膜的质量要求也越来越高,现有的涂料沉积模型和工件曲面造型方法已渐渐不能满足人们的需要,如何找到更加合适的涂料沉积模型和工件曲面造型方法还需不断探索。虽然目前机器人喷枪轨迹生成与优化还不够成熟,但随着计算机视觉与人工智能等新兴技术的飞速发展,结合视觉与AI技术的机器人智能自动喷涂一定会出现,并将完全取代人工喷涂。

