考虑抗弯刚度的悬索桥短吊索索力识别
张 云 刘 涛
(武汉理工大学土木工程与建筑学院 武汉 430070)
拉索是斜拉桥及悬索桥的重要结构构件[1-2],而工程实际中,常常引用不考虑索股抗弯刚度的方式来进行短吊索的索力识别[3-4]。对于悬索桥上的短吊索,其抗弯刚度对索力测试结果影响很大[5-7],若将短吊索索股简化为理想弦振动,则其索力结果与设计值偏差很大。
本文基于吊索的振动方程,推导考虑索股抗弯刚度的索力计算公式,以获得简单准确的短吊索索力识别方法。
1 短吊索索力识别
1.1 理想弦振动
索股的抗弯刚度很小以至于可忽略不计时,此时可将张紧的弦看作是理想的弦,假定弦长为L,线密度为m,索股在微小振动时其拉力不变为F。
运用瑞利-里兹法计算振弦的频率,拉索振动时,拉索的动能和势能相互交替,根据动能守恒原理,可得
(1)
式中:ωn为索股的n阶振动圆频率,其频率fn为
(2)
因此
(3)
工程上一般都取低阶频率,此处采用一阶频率化简得到式(4)的简化算法来计算索力
(4)
1.2 考虑索股抗弯刚度
此时设拉索弦振动方程为
(5)
式中:x为弦的位置;t为时间;An为n阶振幅;L为弦长;ωn为n阶圆频率;φ为初相位。
其最大动能Wmax与最大势能Vmax分别为
(6)
(7)
式(6)与式(7)联立,两者相等,得
(8)

(9)
工程上一般都取低阶频率,此处采用一阶频率化简得到式(10)来计算索力
(10)
2 工程实例
以湖北省恩施州水布垭清江大桥为例,进行索力识别。该桥主跨为420 m,采用高强度镀锌钢丝平行集束为索体的单吊索,短吊索为61丝Φ5.1 镀锌高强钢丝。所有吊索均外包PE层防护。其力学性能见表1。

表1 短吊索单根钢丝力学性能
短吊索截面示意见图1。

图1 吊索截面(单位:mm)
短吊索截面为直径d=59 mm的圆形,则可算得I=594 809.567 1 mm4。弹性模量E=200 GPa,可求得抗弯刚度EI=118.96 kN·m2。
取5根短吊索,其力学参数见表2。利用midas模型建立全桥仿真模型(见图2),进行成桥有限元模型计算,用246个梁单元模拟主塔及刚桁架,344个只受拉用单元模拟主缆及吊索。散索鞍及主塔塔根边界全部约束,主索鞍与主塔塔顶采用主从刚性连接耦合。在自重条件下运行模型,则可得到成桥状态下,所有吊索的索力值。现场实测该5根索股的索股频率值见表3。
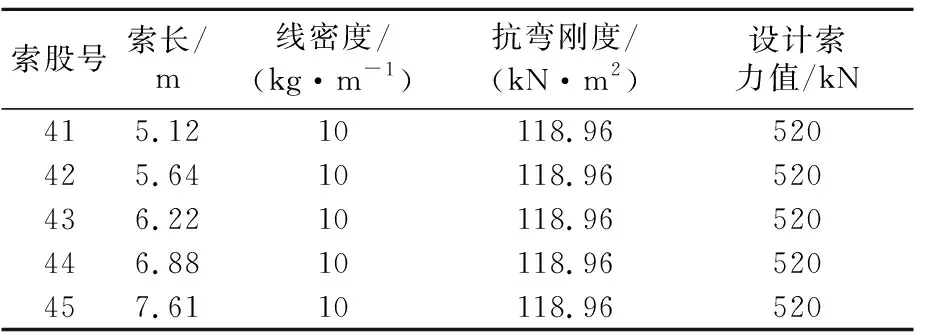
表2 部分短吊索力学参数

图2 清江大桥midas成桥模型

索股号4142434445自振频率/Hz20.9120.4218.7316.9015.37
运用有限元模拟、简化算法式(4)及考虑索股抗弯刚度算法式(10)算得结果与设计索力值对比见表4。

表4 结果对比表
由表4可见,有限元仿真模型结果与设计索力值几乎完全一致。在短吊索索力识别上,41号索股长度最短,简化算法相对误差达到10.4%,但考虑了短吊索的抗弯刚度后,其误差结果只有1.8%。从整体数据上看,考虑抗弯刚度的计算值与设计值的相对误差在2%以下,而简化算法则为5%左右。
3 结论
1) 短吊索索力识别考虑抗弯刚度后,其与设计值的误差值在5%以下,且索长越短,抗弯刚度影响越明显。
2) 考虑短吊索的抗弯刚度的计算结果与有限元计算结果相近,具有实际应用意义。

