机场水泥道面水泥稳定碎石基层应力状态分析

袁 捷 卢迤佳

(同济大学道路与交通工程教育部重点实验室 上海 201804)

水泥稳定碎石基层具有高强度、高刚度及良好的板体性、水稳性，在我国应用广泛，但同时很容易受环境湿度和温度变化产生干缩和温缩应力，继而在强度薄弱处造成开裂。据统计，大部分水泥稳定碎石基层的裂缝间距在50～100 m之间，有的甚至10 m左右就出现裂缝。现有研究对于机场水泥道面水稳基层的应力分析研究较少。为此，本文将针对机场水泥道面结构中典型水稳基层中荷载应力、干缩应力及温缩应力的分布计算做出合理解释，并根据各应力影响因素及发展规律得到一定长度下基层不开裂的理论强度要求。

1 水稳基层应力理论分析

1.1 荷载应力

利用Abaqus建立机场水泥混凝土道面和沥青混凝土道面结构响应分析三维有限元模型，选择的典型道面结构形式和参数见图1，水泥混凝土板平面尺寸为5 m×5 m。王宇翔[1]讨论了有限元各单元优缺点，为了保证计算精度、模型收敛、计算时间较为合理，本文采用C3D8I单元类型。对于水泥混凝土道面，为模拟半无限空间体地基，土基和基层进行了超宽处理，接缝采用Spring 2弹簧单元来模拟，接缝刚度为1 500 MN/m2，弹簧刚度按照节点贡献面积进行分配[2]，单元定义方式见图2。土基与基层之间假定为完全连续状态，基层与面层之间假定为完全光滑状态，最终建立的三维有限元模型见图3。

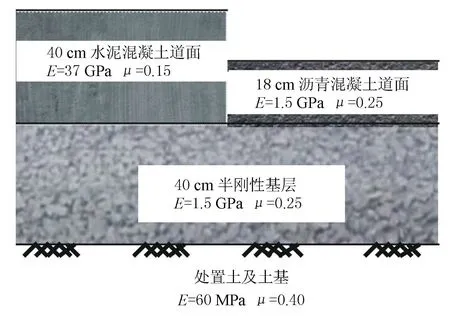
图1 典型机场半刚性基层道面结构

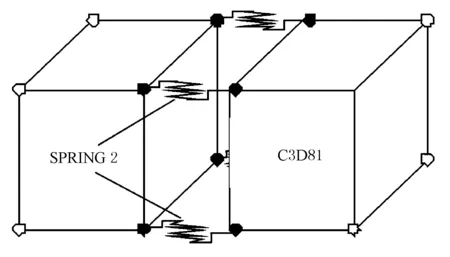
图2 C3D8I及Spring 2单元

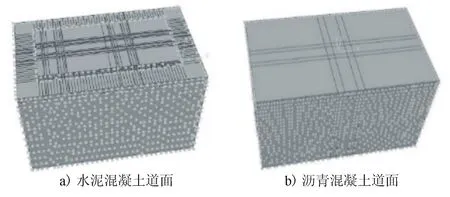
图3 有限元道面结构模型

荷载分别选用B737-300，B747-800和B777-300主起落架，分别代表单轴双轮、双轴双轮和三轴双轮起落架，轮印简化为矩形，具体参数见表1。对于水泥混凝土道面，起落架作用于横缝板边中点；对于沥青混凝土道面，起落架作用于道面中部。

表1 起落架荷载参数

B747-800双轴双轮起落架作用下，基层底面弯拉应力见图4。

图4 半刚性基层底面弯拉应力响应云图

由图4可见，水泥混凝土道面半刚性基层底部最大弯拉应力出现在接缝处，成条带状分布，沥青混凝土道面半刚性基层底部最大弯拉应力出现在轮印正下方；从响应峰值大小来看，水泥混凝土道面半刚性基层底部弯拉应力峰值明显小于沥青混凝土道面。

进一步将不同工况下半刚性基层底面弯拉应力峰值汇总于表2。

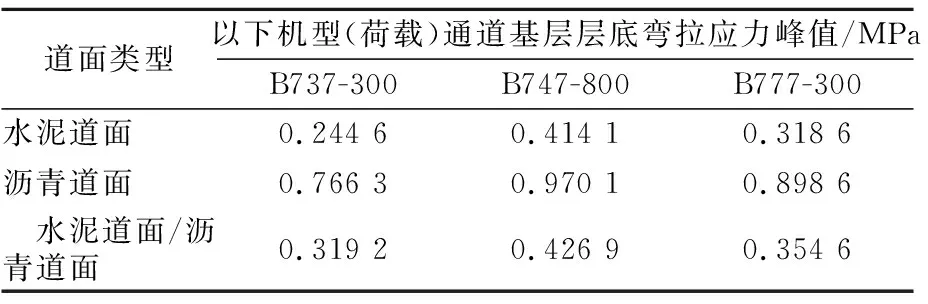
表2 半刚性基层底部弯拉应力峰值

由表2可见，3种机型起落架作用下，水泥混凝土道面半刚性基层底面弯拉应力峰值仅为沥青混凝土道面的30%～45%，均显著减小。

1.2 温缩应力

温缩应力σT参考施为民[3]和梅长今[4]所建立的微分单元体受力理论计算

(1)

由资料可知，αt是一个与温度相关的参数，此处采用试验数据回归下的预估模型[5]

(2)

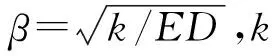
1.3 干缩应力

依据温缩应力求解过程进行干缩应力的理论求解[4]，水稳基层中的干缩应力σG为

(3)

式中：ε(t)为t时间对应的水稳基层收缩应变。

彭全敏[6]对各模型考虑因素及各估算模型计算值与试验值进行了对比，发现B3模型[7]估算结果精度最优。并结合各模型所考虑的因素，本文采用B3模型估算不同龄期下干缩的应变值，最终可得到干缩应力的求解公式

(4)

1.4 综合应力

面层摊铺前，水稳基层中温度及湿度可视面层的情况处理。参考相关资料[8]，同时考虑到温缩与干缩很大程度的相似性，此时综合应力为两者直接加和。

σz=σT+σG

(5)

面层摊铺后，未开裂处基层的应力状态历经过程为：早期温、干缩应力作用下最大不超过劈裂强度σp，后在应力松弛的作用下，早期综合应力减小，最后再承受飞机荷载引起的应力。此处考虑前面有限元分析所得的板底最大弯拉应力σw，故综合应力为

σz=δ·σp+σw

(6)

式中：δ为应力松弛系数，一般可取0.3～0.5[9]。

2 模型验算

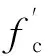
图5 温度分布图

对水稳基层应力的分析可分为2个阶段进行考虑：面层摊铺前和面层摊铺后。

1) 面层摊铺前。取相对湿度h为60%，得到基层干缩应力变化规律，见图6。图6所示若基层不发生断裂，干缩应力随基层长度与干缩时间不断增大，最终趋近一定值。实际中水稳基层一般在完工后10 d左右内部湿度下降速度最快，取干缩时间t为10 d。干缩应力随长度的变化规律如图7实线所示。考虑温缩应力影响，基层内的温度分布按图5所示道面结构中面层的温度数据进行计算，温缩应力随长度的变化规律如图7中虚线所示。

图6 干缩应力变化规律

图7 各应力随基层长度变化规律(t=10)

由图7可见，在长度50～100 m之间，干缩应力处于0.59～0.86 MPa之间，温缩应力处于0.04～0.09 MPa之间，总应力处于0.63～0.95 MPa，基层的应力水平已经超出了水稳基层最低劈裂强度，形成裂缝。这与目前大部分水泥稳定碎石基层的裂缝间距在50～100 m之间的既有事实完全相符。随着基层长度的增加，到300 m左右时，干缩应力与温缩应力增长速度都已经非常平缓，分别趋近于1.1 MPa和0.15 MPa。相比之下，干缩应力是温缩应力的7.3倍，这也说明了在水稳基层形成早期开裂主要是由于干缩应力引起的。

2) 面层摊铺后。基层顶面温度下降约10 ℃，并且变化幅度较大时也只约为2 ℃，温度应力仅为0.025 MPa，为面层摊铺前的16.7%，面层的覆盖明显减弱了温度造成的影响。湿度的变化也已经进入非常缓慢的阶段。按照式(6)，取δ=0.4，得到此时基层综合应力

σz=δ·σp+σw=0.24+σw

(7)

考虑有限元所计算水泥道面3种机型荷载应力：0.24，0.41，0.32 MPa，σz计算结果分别为0.48，0.65，0.57 MPa。可以发现，出于安全考虑所得到的应力满足基层最小劈裂强度，故基本不会产生新的裂缝(除个别结构薄弱区)。相较于1.25 MPa的面层摊铺前综合应力，可以发现摊铺后即便有着荷载的作用，其在结构内部形成的拉应力也只有摊铺前的50%左右，故大量的裂缝形成于面层摊铺前。

3 温缩应力影响因素分析

根据之前推导得到的温度应力计算式(1)和(2)，并假定从基层顶面到底面之间温度梯度为一定值，故以面层摊铺前的温度数据计算温度梯度，并得到温度应力计算式(9)。

(8)

(9)

根据式(9)利用MATLAB分别绘出随着基层长度的增长，不同厚度D(40～32 cm，间隔2 cm)及不同水泥剂量Ce(3%～5%，间隔0.5%)下σT的变化规律，并进行汇总，汇总见表3。表3中每个长度下左列表示的是应力值，右列表示的是该值与D=40 cm，L=300 m对应应力值的比，最下行与最右列表示的是该条件下最大应力与最小应力的差与最大应力的比。

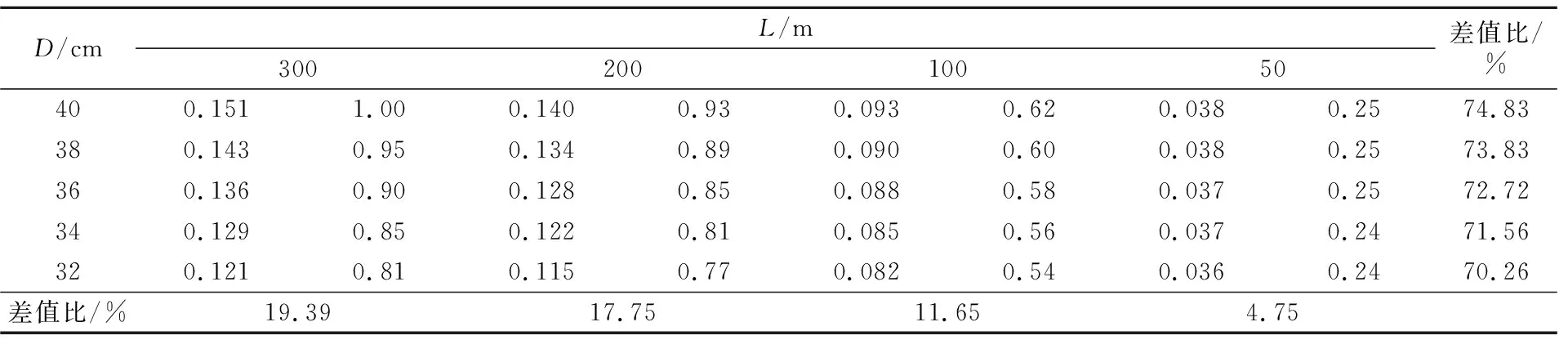
表3 温度应力与基层厚度、长度变化规律

由表3可见，随着基层厚度、长度的增加，温度应力随之增大，基层长度在300 m时趋近于某一定值，即为表3中300 m对应的应力值。当厚度由大变小时，2 cm的厚度差依次对应1%，1.1%，1.2%，1.3%的差值比变化，即厚度越小，其对应力的影响越大。并且随着基层长度的增加，厚度差异的作用也越明显，当L=50 m时，厚度几乎不对应力产生影响。

同理可得，温度应力随水泥剂量和长度的增加逐渐增大，基层长度在300 m时，水泥剂量由低到高对应的温度应力分别为0.139，0.142，0.145，0.148，0.151 MPa，随长度趋近于稳定。而当水泥剂量一定时，沿长度方向的应力变化幅度基本均为75%，同样地，当长度一定时，由于水泥剂量的改变造成应力的改变基本均为8%，每0.5%的变动造成2%的应力幅值改变。

4 干缩应力影响因素分析

水稳基层厚度越厚，则水稳层内的水分越难以挥发，抗干缩能力也越好，故在此不再讨论，如若需要可假定湿度沿厚度方向均匀变化，存在一定湿度梯度，带入分析即可。式(4)中虽未直接体现水泥剂量，但容易得到28 d圆柱体抗压强度设计值与水泥剂量为正比规律，故本节仅重点考虑相对湿度h(50%～90%，间隔10%)和混凝土含水量w(4%～6%，间隔0.5%)对干缩应力造成的影响。由于处理方式一致，故不再累述，直接说明数据结果。

干缩应力与相对湿度成反比，基层长度在300 m时，各相对湿度由低到高对应σG分别为1.199，1.074，0.900，0.669，0.371 MPa，趋于稳定。相对湿度一定时，长度50～300 m的干缩应力增幅恒为45%；基层长度一定时，相对湿度50%～90%的干缩应力增幅恒为69%，即相对湿度与基层长度之间不存在交互作用。

同样可得，干缩应力与含水量成反比，基层长度在300 m时，各含水量由低到高对应应力为0.459，0.587，0.733，0.895，1.074 MPa，并随长度趋于稳定。含水量一定时，长度50～300 m干缩应力增幅恒为45%；基层长度一定时，随着含水量4%～6%的干缩应力增幅为57%，即含水量与基层长度之间不存在交互作用。

5 结论

1) 水泥道面于早期10 d左右形成裂缝，裂缝的间距一般为50～100 m。

2) 在面层摊铺前，基层可视为面层，温缩应力和干缩应力决定了综合应力，导致了绝大多数裂缝的形成；在面层摊铺后，通过有限元建立典型模型得到了水稳基层在飞机荷载作用下形成的荷载应力。此阶段温度应力较小可忽略，非常少量的裂缝形成于此阶段。

3) 温缩应力与干缩应力随基层长度增加而增大，在300 m左右时都会趋近于一定值。根据实验数据分析得到温度应力与厚度、水泥剂量成正比：基层长度越长，厚度影响越大，而水泥剂量影响则与基层长度无关；干缩应力与相对湿度及厚度成反比，与水泥剂量及含水量成正比；相对湿度和含水量的影响与基层长度无关。相比之下，干缩应力的变动幅度更大。

4) 根据实践，若振动拌和和振动压实能提高水稳基层劈裂强度至0.9～1 MPa，即可基本实现裂缝间距为200～300 m，从而增大裂缝间距、减小裂缝数量。