考虑坡顶建筑荷载影响下的公路边坡稳定性分析*

魏小楠 吴维义 杨根兰

(1.贵州省交通规划勘察设计研究院股份有限公司 贵阳 550081； 2.贵州大学 贵阳 550025)

由于受特殊地形地貌影响，在贵州山区，大量居民建筑依山而建，当居民建筑至边坡坡顶边缘的水平距离较近或坡顶建筑荷载较大时，可能导致边坡稳定性降低、边坡滑裂面位置及滑动范围发生改变，从而导致边坡发生过大变形或失稳破坏，因此，在边坡稳定性分析中坡顶居民建筑一般不能忽略。目前，在有关坡顶荷载对边坡稳定性影响的研究中，罗智[1]运用Bishop法对不同分布形式的坡顶荷载作用下的边坡稳定性进行了探讨，总结出不同坡顶荷载位置、大小及长度变化下的边坡稳定性变化规律；夏晓慧[2]采用极限分析理论对边坡的稳定性进行了研究并分析了条形基础的各个参数与边坡安全系数的关系；郑允等[3]基于传递系数法，通过建立坡顶荷载作用下岩质边坡倾倒破坏地质力学模型，提出了考虑坡顶荷载作用的边坡倾倒破坏的解析分析方法，从而推导出了坡顶荷载作用下反倾边坡坡脚剩余下滑力和维持边坡稳定所需要的支护力的计算公式；黄嘉等[4]以实际工程为例，将上部建筑荷载简化作用在桩基础上，并分析了桩端进入边坡潜在破裂面以下和位于潜在破裂面以上2种情况下边坡的稳定性系数，得到桩端进入潜在破裂面以下时，边坡的稳定性系数比桩端位于潜在破裂面以上时提高4倍以上。上述学者多采用传统的理论方法研究在坡顶荷载作用下的边坡稳定性，鲜有学者对不同开挖阶段下边坡稳定性进行分析。本文以贵州省某公路边坡为例，在掌握边坡地质参数的前提下，采用FLAC3D软件模拟边坡在坡顶建筑荷载影响下的各开挖阶段的稳定性，以期为类似工程设计提供参考。

1 工程概况

该边坡位于贵州某二级公路段内，场区地貌类型为峰丛-溶蚀地貌，场地最低点绝对标高约926.38 m，最高点绝对标高约1 025.35 m，相对高差98.97 m，局部地形高差变化较大。

根据区域地质资料，场区位于扬子准地台，黔北台隆，遵义断拱，鸭溪向斜北翼，鸭溪向斜为北北东-南南西向向斜，未见有活动性断层通过，场区地质构造较简单，区域构造较稳定。上覆第四系黏土，厚度约为0.5 m，下覆为二叠系上统龙潭组(P2l)炭质页岩，黑褐色，强风化～中风化，薄层～中厚层状构造，岩层产状为172°∠45°，线路走向227°，岩体产状与线路走向呈斜交，岩体较破碎，节理发育，无软弱结构面，其中强风化层厚1.3～1.5 m。边坡附近无江河流经，地表水呈季节性变化，地下水类型主要为裂隙水，水文地质条件较简单。根据GB 18306-2015 《中国地震动参数区划图》，场区地震基本烈度为VI度。

该边坡按原设计开挖后，将形成高32 m的3级边坡，坡面均采用预应力锚索框架梁防护，框架梁按3 m×4 m布置，梁截面为400 mm×400 mm，单根锚索设计锚固力800 kN，居民建筑基础距离边坡坡口线最近约2 m，当逆向开挖至第二级坡脚时线路发生调整，使第一级边坡坡顶距第二级边坡坡脚距离由原设计的2 m调整为8 m，设计方建议继续施加第二级边坡的框架锚索。

边坡典型断面见图1,边坡支护措施的布置情况见图2。

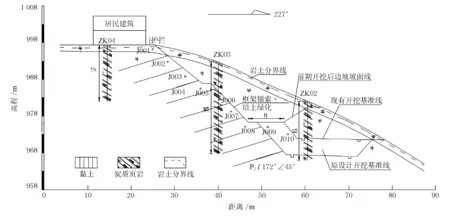
图1 边坡典型断面设计防护图

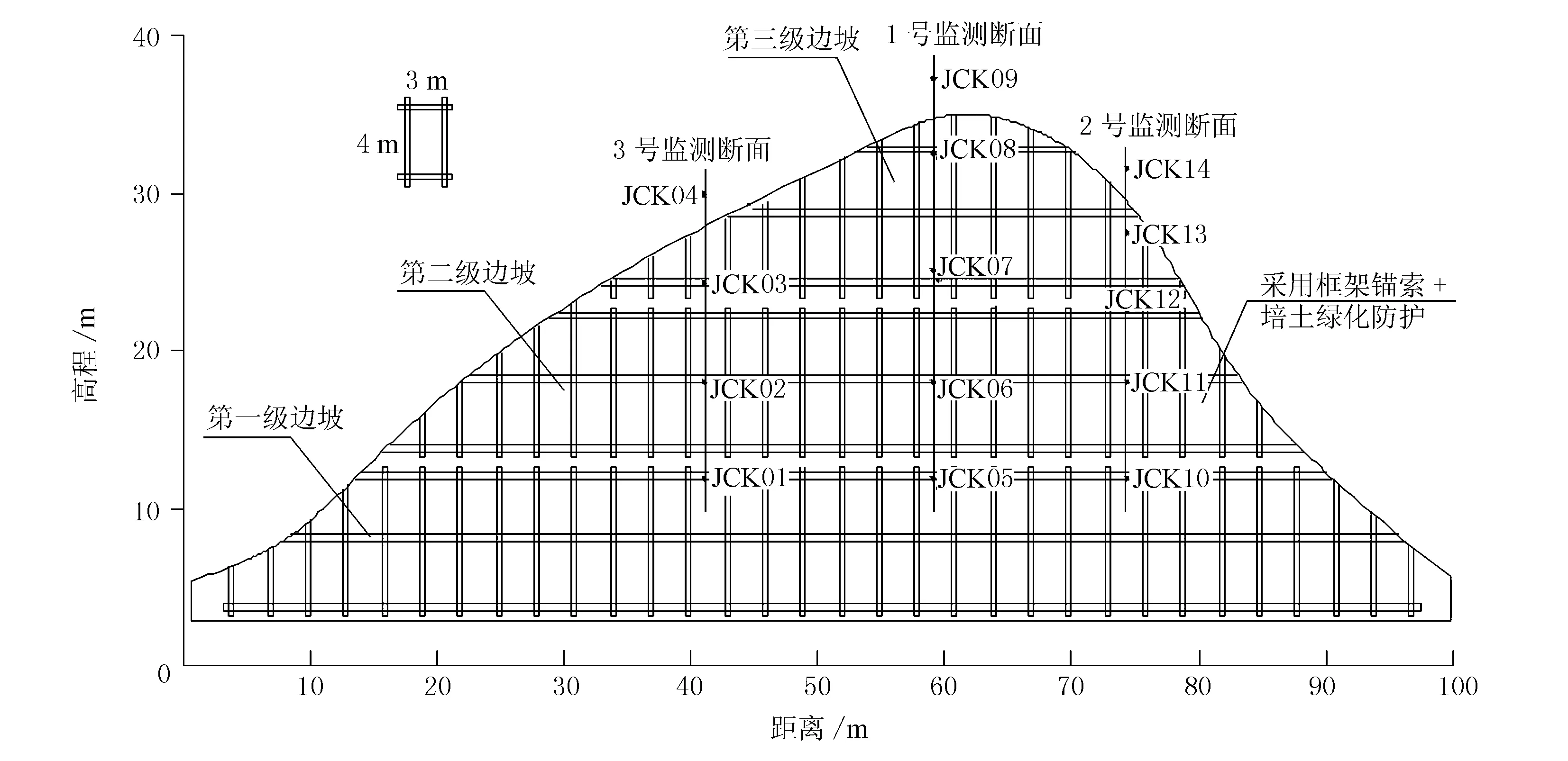
图2 边坡立面设计图(原设计)

2 计算模型及计算方案

2.1 计算模型建立

对边坡典型断面进行适当简化，取计算模型长80 m、竖直高35 m、厚度12 m；采用ANSYS-FLAC3D的建模思路，得到边坡的三维计算模型，见图3。

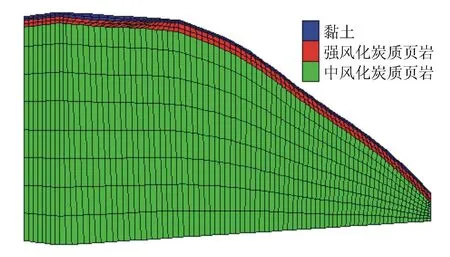
图3 边坡三维计算网格

该模型共有7 392个单元、34 671个节点。预应力锚索与框架梁的建立方法参见文献[5]，房屋荷载换算后分布在条形基础上，最后采用apply nstress语句施加。模型底面固定，背面及左右两侧法向约束，坡体表面为自由面。

2.2 计算参数选取

将房屋荷载简化作用在基础上,基础为条形基础(见图4)，按照GB 50009-2012 《建筑结构荷载规范》[6]进行简要计算如下。

房屋为2层的砖混结构，墙厚度按二四墙考虑，墙高8 m，周长60 m，墙体材料为普通砖，重度为18 kN/m3；屋面为钢筋混凝土现浇面板，厚20 cm，重度为24 kN/m3，则房屋永久荷载

W1=γV=0.24×60×8×18+0.2×12×8×24= 2 534.4 kN

(1)

作用在基础上的荷载除永久荷载外，还有人为因素等造成的活荷载，同时还需考虑风、雪等其他荷载，综上，本居民建筑外荷载按2 kN/m2计算，最终得到外荷载

W2=2×12×8×2=384 kN

(2)

房屋基础形式为0.5 m宽的条形基础，将房屋荷载按均匀分布形式全部简化作用在基础上(见图5)，则基础压力

p=(2 534.4+384)/(60×0.5)=97.28 kPa

(3)

计算时按100 kPa考虑。

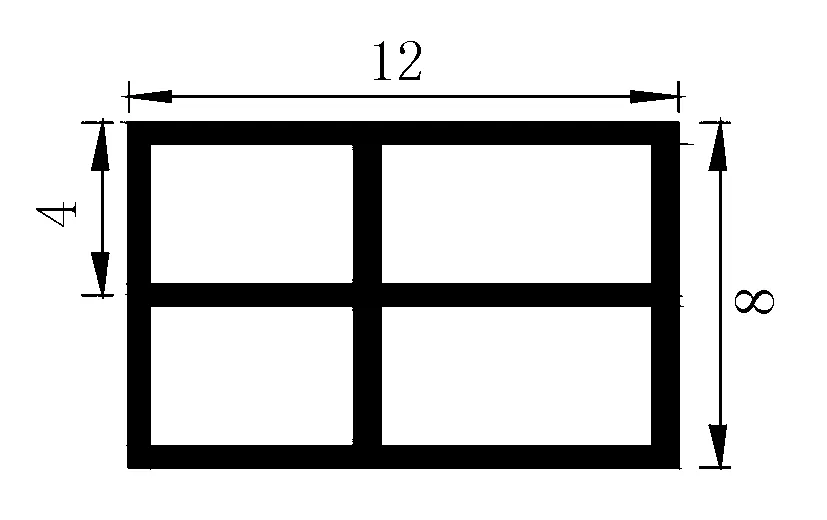
图4 居民建筑基础形式(单位:m)

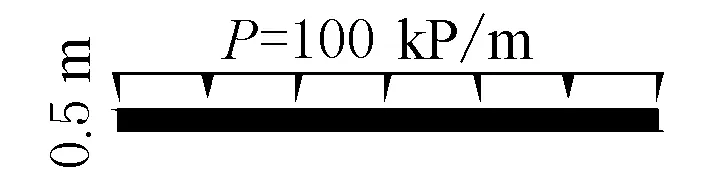
图5 基础荷载分布

依据地勘报告与相关工程经验确定边坡坡体参数见表1；锚索及框架梁所取参数见表2、表3。

表1 岩土体力学参数

表2 框架梁计算参数

表3 锚索计算参数

2.3 计算方案

为验证原设计方案的合理性，根据边坡的现场施工情况，先计算边坡的初始位移、应力场，然后考虑后期边坡变形因素主要为开挖，因此需清除边坡初始位移、应力场，最后按逆作法分级开挖、分级支护，具体如下：

1) 按原设计开挖基准线进行计算。该方案具体分为4个小的计算方案，第一为按原设计开挖后坡面不支护(①方案)；第二为按原设计开挖后坡面均采用框架锚索支护(②方案)；第三为根据现场情况，在第三级边坡坡面施加框架锚索，第一、二级不施工(③方案)；第四为得出坡顶荷载是否对边坡的稳定性存在不利影响，取消①方案坡顶荷载(④方案)。

2) 按现有开挖基准线进行计算。该方案具体分为4个小的计算方案，第一为按设计开挖后第二、三级坡面采用框架锚索防护(⑤方案)；第二为根据现场情况，只在第三级边坡坡面施加框架锚索(⑥方案)；第三为坡面均不施加防护措施(⑦方案)，第四为边坡开挖至前期开挖后边坡坡面线就不再开挖，以此分析第一级边坡开挖对第二、三级边坡的稳定性影响(⑧方案)。

3 结果与分析

采用强度折减法分别计算上述8种计算方案下边坡的稳定安全系数，将其绘制成图6。

图6 不同计算方案的边坡稳定安全系数

由图6可见，①方案的稳定安全系数1.15明显小于④方案的稳定安全系数1.27，由此得出在坡顶荷载作用下，边坡稳定性向不利方向发展；在原设计开挖基准线下坡面均施加框架锚索后边坡稳定性满足规范[7]要求，说明在该工况下原设计方案合理；当按现有开挖基准线进行施工时，由⑥方案与⑧方案计算结果可知，由于第一级边坡坡口线距第二级边坡坡脚距离由原来的2 m变为了8 m，其开挖对第二、三级边坡的稳定性影响较小，加之第二、三级边坡自身稳定性良好，因此可取消第二级坡面设计的框架锚索。

边坡最终施工方案(⑥方案)X方向的位移云图如图7所示，并运用FISH语言编写命令提取该计算方案下边坡特征点的水平位移值(监测点的布置情况见图1)，绘制成图8。

图7 边坡水平位移等值线图(单位：m)

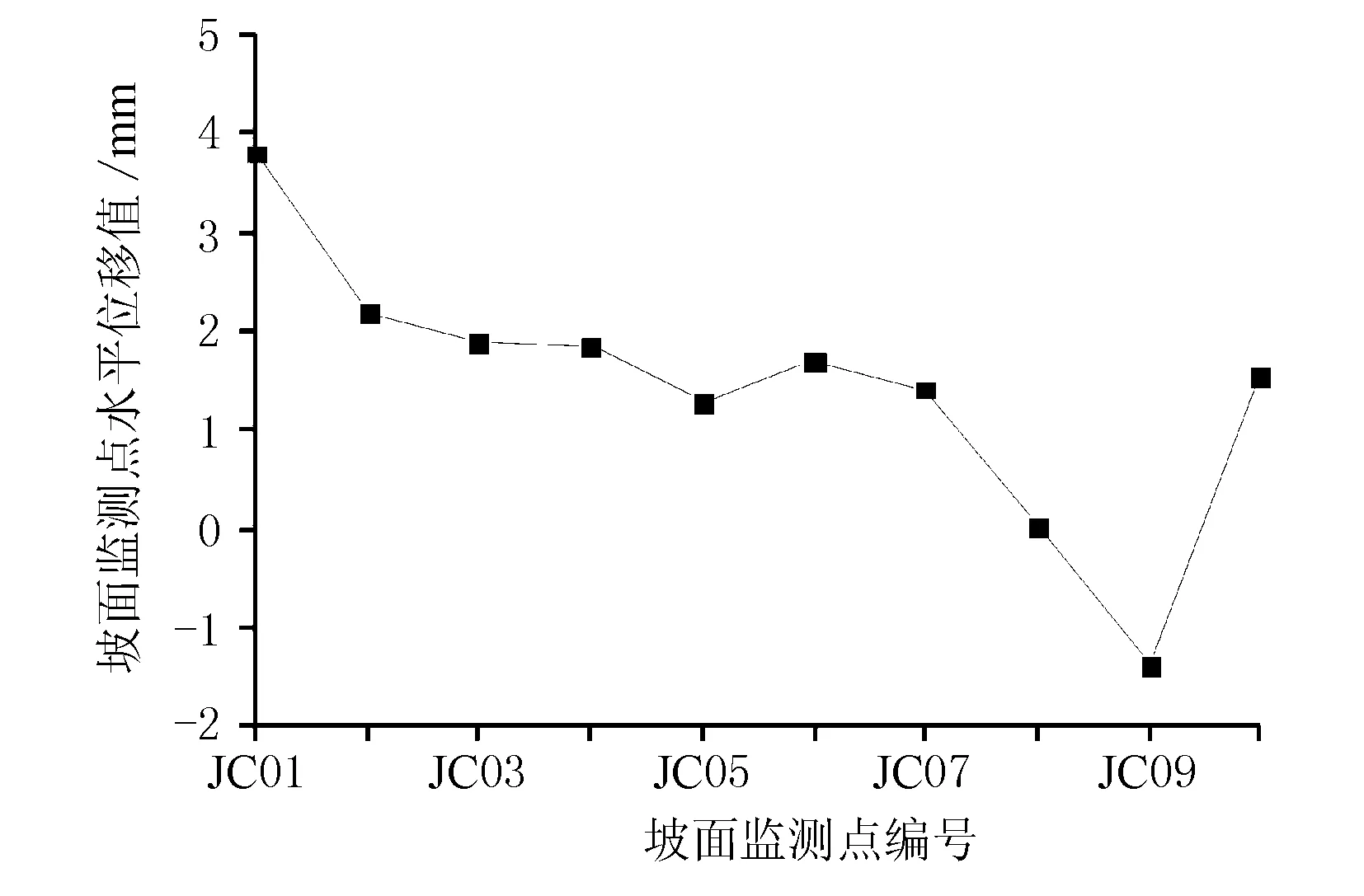
图8 坡面监测点水平位移值

由图7、图8可见，优化后边坡的最大水平位移值较小，边坡稳定性良好，由此得出取消第二级坡面的框架锚索是可行的，同时，考虑优化设计时第三级边坡坡面的框架锚索已全部施工完毕，利用其对边坡加固不仅可以解决第三级边坡岩体风化等问题，同时可提高边坡的稳定安全系数，进一步保障坡顶居民建筑的安全。

4 地表位移监测数据分析

地表位移监测可以直观反应边坡的变形情况。在本项目施工完毕后，根据边坡现场工程条件，布设了3个监测断面共计14个地表位移监测点(见图2)对边坡实施工后监测，其中，1号监测断面的监测成果见图9、图10。

图9 X方向时间-位移曲线

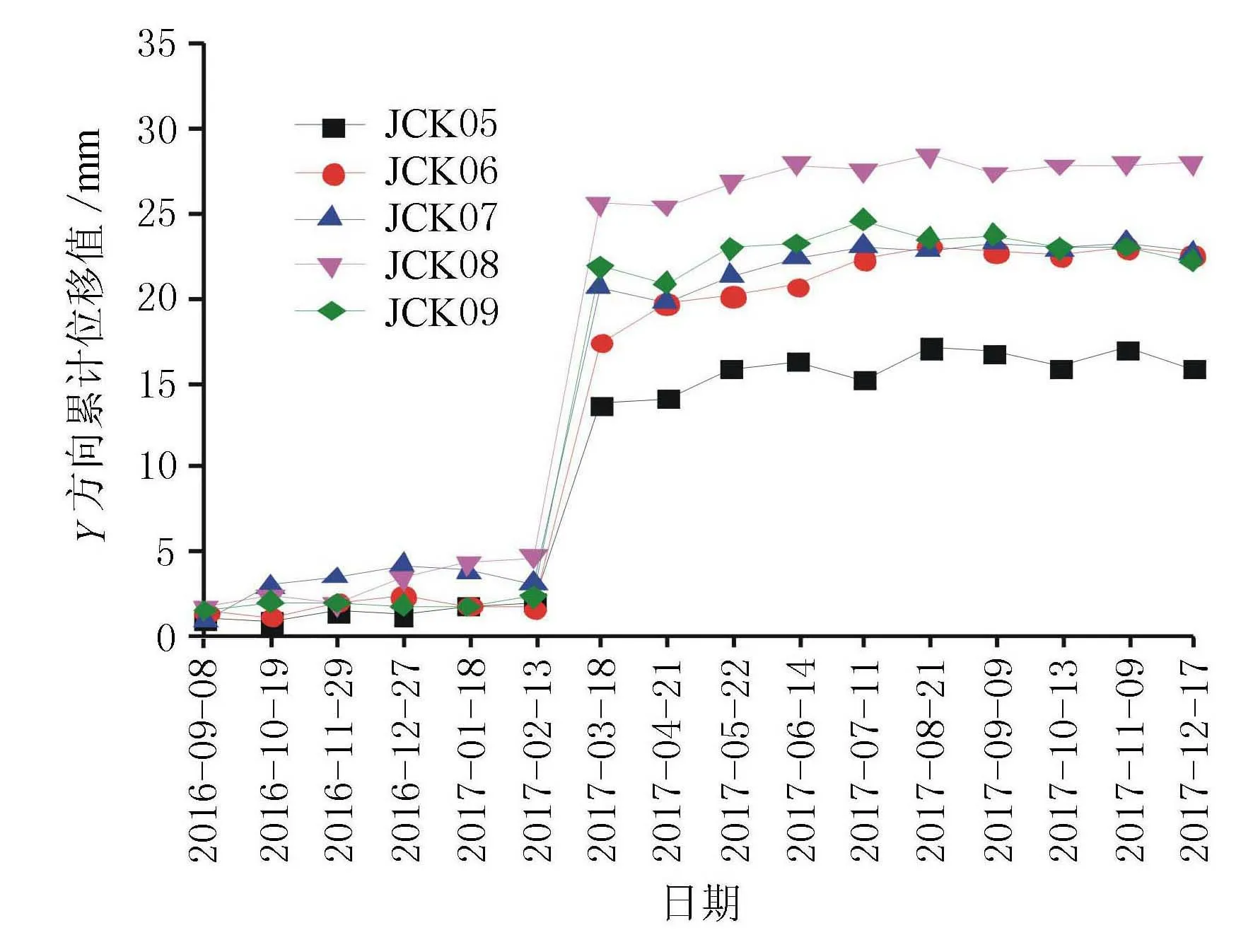
图10 Y方向时间-位移曲线

从图9、图10可见，边坡在支护后的2016年9月8日-2017年2月13日期间，各监测点的位移-时间曲线变化平稳，说明期间边坡稳定性良好；2017年2月13日-3月18日期间，坡面各监测点的位移均发生突变，分析原因为边坡支护后受第一场连续大雨影响，坡体岩土体孔隙水压力增大、有效应力降低，边坡发生了应力调整，此时，地表巡视发现边坡坡面多处出现了细微变形，期间根据现场情况加密了观测频率，随后监测数据逐渐趋于平稳，说明边坡得到了有效的治理。

5 结论

1) 根据坡顶居民建筑的实际情况，将房屋荷载全部简化作用在条形基础上，并按照GB 50009-2012 《建筑结构荷载规范》对荷载作了简要计算，得到每延米基础上的荷载为100 kPa。

2) 在原设计方案条件上，通过模拟相同工况时坡顶是否有居民建筑下的边坡稳定性状况，得到考虑坡顶荷载时边坡的稳定性系数为1.15，小于不考虑荷载时的1.27，得出在坡顶荷载作用下，边坡稳定性将向不利方向发展。

3) 在改线后的设计方案条件下，由于第一级边坡坡口线距第二级边坡坡脚距离由原来的2 m变为了8 m，其开挖对第二、三级边坡的稳定性影响可以忽略，加之第二、三级边坡自身稳定性良好，因此可取消第二级坡面设计的框架锚索，从而节约大量的工程建设成本。

4) 边坡施工完毕后，为保障道路安全运营与居民建筑安全，在坡面布设了3条监测断面，共计14个地表位移监测点，通过监测数据可知，边坡在施工后一直稳定，直到第一场连续大雨时坡面位移才发生突变，但其后逐渐恢复平稳，由此得出优化后的边坡治理方案合理。