低轨道卫星随机接入系统中多用户检测算法

鲁大伟，王奇伟，任光亮

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

物联网自提出以来，逐渐成为国内外热点研究的问题之一．物联网被广泛应用于环境监测、灾害预测及油气勘探中[1-2]．在这类场景中，物联网设备通常分布在广阔或遥远的区域，地面网络难以对这样大范围或特定的区域提供数据采集和传输服务，而卫星网络可以很好地弥补地面网络在覆盖能力上的缺陷[3]．在卫星物联网中，采用随机接入方法可以避免过高的接入时延和获得较高的吞吐量．

在传统的随机接入方法中，如Aloha和时隙Aloha，用户分组的碰撞概率随着用户数增加而不断提升，由此引起的重传将会导致整个系统的数据传输出现较大的延迟．在卫星网络中，为了避免由于频繁重传而导致的大接入时延，一些新的随机接入方法相继被提出，如竞争解决分集时隙Aloha(Contention Resolution Diversity Slotted Aloha，CRDSA)[4]和不规则重复时隙Aloha(Irregular Repetition Slotted Aloha，IRSA)[5]．CRDSA类随机接入方法的基本原理是，每个用户发送多个重复的数据分组，接收机逐个检测未发生碰撞的分组，并进一步消除已检测分组的所有副本，从而达到干扰消除的目的，提高分组的检测概率．在干扰消除的过程中，为了准确地消除译码分组，接收机需要有效的信道估计来获取准确的信道状态信息．否则，错误的信道状态信息会导致译码分组不能准确消除，剩余误差叠加在未译码分组上，从而影响系统干扰消除的性能，降低分组检测概率[6-7]．

目前，关于卫星网络中新随机接入方法下的多用户检测，已有部分文献开展了研究．文献[6-7]基于CRDSA类随机接入协议，提出了一种基于最大期望(Expectation Maximization，EM)算法的信道估计算法，并通过干扰消除实现分组检测译码．文献[8-9]在CRDSA类随机接入协议出现死锁问题时，通过相关定位分组位置，然后利用校正参数合并分组并译码．文献[10]针对增强竞争解决Aloha(Enhanced Contention Resolution Aloha，ECRA)[11]协议，提出非相干软相关及干扰感知软相关算法用于检测分组．然而，上述文献都只考虑了简单的信道模型．考虑到低轨道(Low Earth Orbit，LEO)卫星具有传播时延短和路径损耗低的特点，并已经广泛应用于中等规模业务量的卫星通信领域．因此，LEO卫星具备与低速率、低时延、广覆盖的物联网相结合的天然优势．但是，由于LEO卫星近地飞行的角速度极大，高速移动带来的最大多普勒频移可达几十千甚至上百千赫兹，并会导致信道的快速时变问题，而文献[6-10]中的准静态信道模型并不能够描述这样的信道．因此，针对LEO卫星系统中信道快速时变的特点，文中基于CRDSA类随机接入协议重新设计了一种多用户检测方案．该方案采用基扩展模型(Basis Expansion Model，BEM)来建模多用户信道，并通过最大似然(Maximum Likelihood，ML)算法联合求解多用户的基系数，通过基系数拟合出各用户的时变信道，最后重构出所有干扰用户分组并进行干扰消除，对干扰消除后的剩余信号进行译码．利用译码比特及各用户训练块和已检测用户数据重复上述信道估计及干扰消除过程，以此提高分组的检测概率．

1 系统模型

1.1 CRDSA类协议多用户检测

图1 CRDSA随机接入示意图

图1以CRDSA随机接入协议为例，阐述了CRDSA类随机接入协议多用户分组检测原理．用户1、用户2和用户3分别在一帧中两个不同时隙上发送同一分组的两个副本．时隙3上只有用户1分组的某个副本1b，接收机首先检测分组1b并译码；然后使用分组1b的译码结果重构出时隙1上的分组1a，并进行干扰消除，于是时隙1上的分组2a成为无碰撞分组，接收机再检测分组2a并译码．

考虑具有几十千赫兹多普勒频移的LEO卫星信道，各用户在不同时隙上的信道参数差异明显．因此，接收机需要准确地估计出各用户在各个时隙上的信道参数；否则，错误的信道估计会导致重构干扰分组时引入较大的剩余干扰，从而恶化分组检测性能．

图2 用户分组结构

1.2 系统设置

考虑一个时隙内有K个用户的情况，假设各用户分组已经同步，接收机已检测出该时隙的用户数，并且用户1，2, …，K-1 分组均已成功检测译码．现在需要准确地估计出所有用户的信道参数，然后重构出用户1，2, …，K-1 分组并进行干扰消除，最后检测译码出用户K分组．用户的分组结构如图2所示．

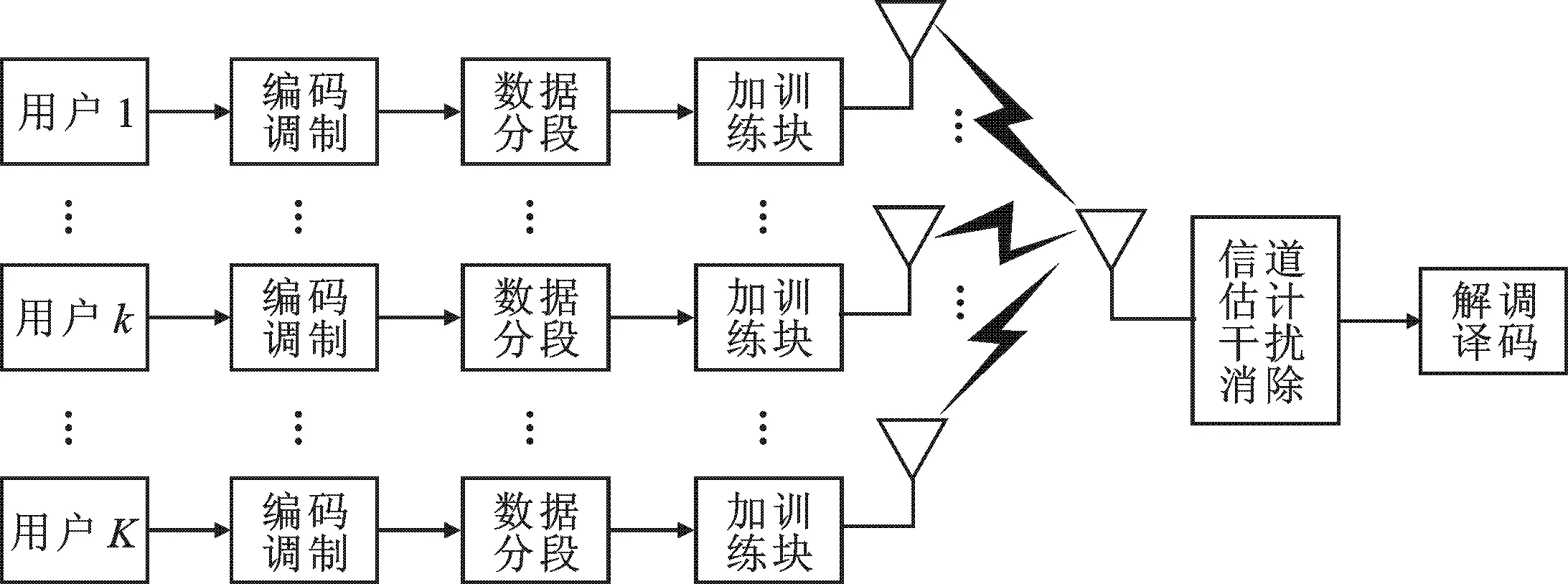
图3 多用户系统模型

1.3 信号模型

文中设计的多用户系统模型如图3所示．

(1)

其中，sk(n)=0；∀n<0；L为多径莱斯信道径数；hk(n;l)为第k个用户的第l条径在n时刻的信道系数；dl为第l条径的时延；d0=0，表示直射径；w(n)为加性高斯白噪声(Additive White Gaussian Noise，AWGN)．对于l=1，2, …，L-1，hk(n;l)为瑞利衰落信道系数，其自相关函数为[12]

(2)

采用ITU-R M.1225中卫星多径信道模型，其他径与直射径的最大功率比为 -34 dB，完全可以忽略，从而将多径信道模型简化为单径信道模型，即

(3)

2 多用户检测算法

2.1 基于迭代信道估计及干扰消除的多用户检测算法

BEM提供了时变信道的简便表示，令hk=[hk(0),hk(1), …,hk(T-1)]T，表示第k个用户在整个用户分组上的信道系数矢量．令μq= [μq(0),μq(1), …,μq(T-1)]T，表示第q个基函数矢量，则有[13]

(4)

其中，bqk为第k个用户的第q个基系数；Q为基函数个数，Q≥2fdTsT+1；fd为多普勒频移；Ts为采样间隔．采用BEM表示各用户的时变信道，则有

(5)

(6)

(7)

其中，O=[St1∘Ut，St2∘Ut，…，Stk∘Ut，…，StK∘Ut]，Stk为stk重复Q次，∘表示Hadamard积．则式(7)可变为

(8)

其中，上标H表示共轭转置，上标-1表示矩阵的逆．

然后，利用各用户的基系数估计值拟合出各用户的时变信道，即

(9)

最后，重构出干扰用户分组并进行干扰消除，即

(10)

2.2 算法复杂度

假设用户训练块总长为V，迭代次数为G．算法的复杂度包含多用户基系数的联合求解及干扰消除．多用户基系数的联合求解包含3次矩阵相乘和1次矩阵求逆，矩阵求逆的复杂度为O((KQ)3)．在初始信道估计中，3次矩阵相乘至少需要 (2V+ 1)(KQ)2+ (2V- 2)KQ次加法或乘法运算；在重复信道估计中，3次矩阵相乘至少需要 (2T+ 1)(KQ)2+ (2T- 2)KQ次加法或乘法运算．干扰消除需要 2TKQ+TK-T次运算．综上，算法复杂度为O(G(KQ)3)+O(GT(KQ)2)．通常KQ远小于T，算法复杂度可简化为O(GT(KQ)2)．仿真表明，一次迭代后信道估计精度几乎不再提升，故算法复杂度远小于O(T3)．

2.3 信道估计的克拉美罗界

(11)

其中，E表示数学期望；信息矩阵JT=JD+JP，矩阵JD是数据信息矩阵，它表示从观测数据中获得的信息; 矩阵JP是先验信息矩阵，它表示从先验知识中获得的信息．矩阵JD的第i行第j列元素可表示为

(12)

其中，x表示观测矢量，θi表示θ的第i个元素．矩阵JP的第i行第j列元素可表示为

(13)

其中，I表示训练块时刻的索引集合，Il表示索引长度，N0表示噪声功率．

不同用户的信道系数相互独立，且信道系数的实部与虚部也相互独立，则有

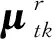
(16)

其中，Ψrkn，rkn和Ψikn，ikn分别表示Ψ的第Ilk-Il+tn行、第Ilk-Il+tn列元素和Ψ的第IlK+Ilk-Il+tn行、第IlK+Ilk-Il+tn列元素，其中tn表示n时刻对应的矩阵Σ-1的行下标或列下标．

3 仿真结果

图4 误包率性能

仿真中采用ITU-R M.1225中卫星多径信道模型，莱斯因子为 7 dB，多普勒频移为 35 kHz，用户采用码率为 1/2 的Turbo码及正交相移键控(Quadrature Phase Shift Keying，QPSK)调制．分组前导、导频、后导长度分别为40、12、12，在包含456个符号的数据中均匀插入7块导频，基扩展模型采用离散椭圆基扩展模型(Discrete Prolate Spheroidal Basis Expansion Model，DPS-BEM)，基函数个数为11．文献[6-7]的算法是一种适应准静态信道的算法，笔者设计的算法是一种适应时变信道的算法．图4为各种算法在两用户及三用户情况下的误包率(Packet Error Rate，PER)性能曲线．由图4可以看出，在相同条件下，适应时变信道的算法均明显优于适应准静态信道的算法．并且，无论是适应时变信道的算法，还是适应准静态信道的算法，利用译码后数据作为导频的迭代算法均相对于仅使用训练块的非迭代算法有较大提升．随着用户数的增加，适应时变信道的算法性能有轻微下降，而适应准静态信道的算法性能则下降明显，适应时变信道的算法更能容忍多用户．随着信噪比的增加，适应时变信道的算法性能提升更为迅速．适应时变信道的算法能更好地工作于具有高信噪比的多用户场景．

图5为各种算法在两用户及三用户情况下的信道估计均方误差(Mean Square Error，MSE)性能曲线．图5中标记了利用训练块进行初始信道估计的克拉美罗界．由图5可以看出，适应时变信道的算法相对适应准静态信道的算法有较明显的优势．图6为在 10 dB 信噪比下，各种算法在CRDSA协议下的吞吐量性能曲线．吞吐量定义为成功译码用户数与时隙数之比，归一化负载定义为用户数与时隙数之比．由图6可以看出，在相同条件下，适应时变信道的算法均优于适应准静态信道的算法．由于CRDSA协议理论吞吐量的限制，适应时变信道与适应准静态信道算法之间的性能差异在非迭代情况下更为明显．

图5 信道估计均方误差性能图6 吞吐量性能

4 结 束 语

针对LEO卫星场景，文中设计了一种迭代信道估计及干扰消除算法来进行多用户检测．仿真结果表明，该算法在多组性能方面均优于已有算法的．该算法适用于具有较高信噪比及大多普勒频移的多用户场景．