一种耦合深度信念网络的图像识别方法
马 苗,许西丹,武 杰
(1. 陕西师范大学 现代教育技术教育部重点实验室,陕西 西安 710119;2. 陕西师范大学 计算机科学学院,陕西 西安 710119)
近年来,随着深度神经网络的深入研究与计算能力的不断发展,深度网络的层数从2012年AlexNet模型的8层增加到2015年ResNet模型的 1 202 层[1-2].一般来说,使用深度神经网络识别图像时,网络的层数越多,能学习到的图像特征越高级,识别性能也越好.但是,仅仅增加网络层数会产生以下问题: 一是网络参数随层数增加呈现指数级增长,导致网络训练所需的样本量迅速增大,因此,在样本数据有限的情况下,网络可能无法达到最佳收敛状态; 二是由于网络层数增多,网络训练所需时间也会变得更长,且对硬件环境要求也会提高; 三是在反向传播时,随着网络深度增加,最初几层神经元的更新权重幅值急速衰减,使得网络不能得到有效学习,这种问题被称为梯度消失问题.
作为深度学习中的主流算法之一,深度信念网络(Deep Belief Network,DBN)利用受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)对参数进行初始化,可以有效地避免参数训练陷入局部最优的问题.然而,随着深度的增加,DBN也存在梯度消失问题[5-6].
针对上述问题,笔者将“跨层”连接引入到DBN中,提出了一种耦合深度信念网络(Coupled-Deep Belief Network,C-DBN)的图像识别方法.从本质上看,使用一次“跨层”连接的DBN网络可分解为两个相互耦合的DBN网络,因此,称该网络为“耦合深度信念网络”.同时,文中以一个5层DBN结构为例,对比分析DBN和C-DBN在ASL数据集和MNIST数据集上的识别性能,讨论C-DBN中“跨层”连接的有效性和其主、次线耦合比例对网络性能的影响.
1 深度信念网络
DBN是文献[5]于2006年提出的一种深度学习算法,该网络由一系列级联的RBM和一个分类器组成.本质上,RBM是基于概率生成模型建立数据与标签之间的联合分布,通过对比散度(Contrastive Divergence, CD)[7]算法更新网络参数.目前,它已成功应用在图像识别、文本分类和语音识别等领域[8-12].
DBN网络参数的学习采用逐层训练的模式进行,包括无监督训练和有监督微调两个部分.具体来说,先将训练样本输入到第1层RBM,待该层RBM参数学习达到稳定后,将其隐含层输出作为下一层RBM的输入,通过不断地堆叠RBM并向前传递实现DBN网络参数的无监督学习; 在有监督微调阶段,利用类标信息,以式(1)为目标函数,采用BP算法对网络参数进行更新.

(1)
其中,θ={W,b,c},W为权值,b为可视层偏置,c为隐含层偏置,v为可视层分布,α为学习率.对于某个样本vi,其参数的偏导数为
其中,E(v,h|θ)为给定参数θ的能量函数,·P表示分布P的数学期望,P(h|vi,θ)表示隐含层的概率分布,P(v,h|θ)表示可见层与隐含层的联合分布.通过CD算法,对于每一个参数,式(2)可表示为
2 耦合深度信念网络
2015年,文献[2]提出ResNet模型.该网络通过引入残差子模块缓解了因网络深度增加带来的网络学习性能退化问题,并在图像分类、目标检测和语义分割等领域中都取得很好的成绩[13].图1为一个残差子模块.其中,x为残差子模块的输入,H(x)为输出,残差函数F(x)=H(x)-x.

图1 残差子模块
与传统深度神经网络相比,ResNet模型的主要特点如下:
(1)“跨层”连接.传统深度神经网络在增加网络深度时并没有涉及“跨层”连接.这使得传统深度神经网络在反向传播过程中会出现因层数过深带来的梯度消失问题.ResNet模型通过引入“跨层”连接有效地避免了该问题,提高了网络的学习能力.
(2)“+”操作.底层特征跨层向更高层传递时,有多种融合方式,如相乘、相加等.ResNet模型中通过将经过主线与次线的特征进行求和来构建网络子模块.
综上所述,ResNet模型之所以能在较深的网络层数下获得较好的性能,其主要原因是“跨层”连接的使用有效地缓解了反向传播过程中出现的梯度消失问题,使网络更好地完成参数更新.因此,笔者将其应用于DBN中,设计并实现了C-DBN.C-DBN的网络结构如图2(a)所示.
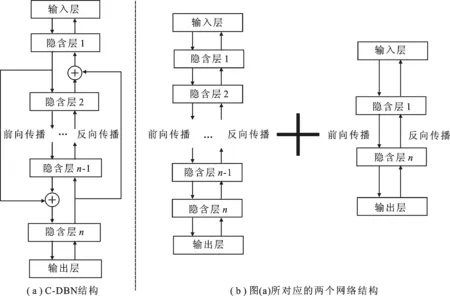
图2 C-DBN网络结构
图2(a)给出了一个引入单个“跨层”连接的DBN网络结构.本质上来看,该网络可看作是一个较深的DBN网络与一个较浅的DBN网络耦合所形成的一种耦合网络,如图2(b)所示.这里考虑到网络不同层次特征学习的尺度差异性及不同尺度特征在图像识别中的贡献,将跨层“⨁”处的传播方式定义如下:
(1) 前向传播过程.训练样本进入输入层后,在某一个隐含层h+1 上会产生一条次线,将其提取的特征与第h+n-1 个隐含层产生的特征联立起来作为第h+n个隐含层的输入,即
Hh+n=(Hh+1,Hh+n-1) ,
(6)
其中,Hh+1、Hh+n-1和Hh+n分别为隐含层h+1层、h+n-1层和h+n层上的特征矩阵.显然,利用特征联立的方式可以将不同层次的特征表征共同输入到下一层进行学习.


(7)
其中,Gh+1、Gh+2和Gh+n分别为隐含层h+1、h+2和h+n上的梯度矩阵,p、q分别为主、次线对应的梯度矩阵耦合比例因子,耦合比例表示为(p∶q).
3 实验结果与分析
3.1 实验数据
文中所用到的实验数据有ASL数据集和MNIST 数据集.ASL数据集是Pugeault等于2011年公布的手势图像数据集,其中以静态图像的形式提供了24个英文字母(英文字母J和Z除外)的手势图像约 60 000 张.为了保证每类手势的样本图像数量一致,以数量比较少的类别数为依据,每个手势图像选择 2 100 张,形成文中实验的训练样本集为 50 400 张(24个英文字母,每个 2 100 张); 类似地,获得测试样本集为 6 000 张(24个英文字母,每个250张),每张图像尺寸均归一化为 32× 32.MNIST数据集来自美国国家标准与技术研究所,由250个不同人手写的数字图像构成,共 70 000 张.文中实验中,该数据集训练样本集为 60 000 张,测试样本集为 10 000 张,每张图像尺寸为 28× 28.
这里,以一个5层的DBN为例进行分析.通过大量实验,笔者发现当DBN的各隐含层节点数分别设置为600、200和100时,网络性能最佳.
3.2 耦合深度信念网络中跨层连接的有效性分析
为分析C-DBN网络结构的有效性,笔者将具有相同深度及节点数且在各自最优参数设置下的DBN和C-DBN进行比较,图3(a)为两种网络在ASL数据集上随迭代次数增加其识别性能的变化曲线,图3(b)为两种网络在MNIST数据集上的图像识别率曲线.

图3 DBN与C-DBN图像识别率对比
由图3可知,随着迭代次数的增加,两种网络的性能曲线都呈现先上升、后平稳的趋势.对于ASL数据,DBN迭代20次时的识别率约为80.13%,C-DBN迭代10次就能达到约81.69%.DBN迭代100次时开始收敛并在迭代200次时识别率约为95.78%; 而C-DBN迭代50次时开始收敛并在迭代200次时识别率约为97.07%.对于MNIST数据集,两种网络性能表现相当,且在1次迭代之后,DBN和C-DBN的识别率均达到90%以上.然而,经过仔细对比,可以看出C-DBN的总体性能仍优于DBN的.具体来说,DBN迭代40次时识别率约达98.52%并收敛,而C-DBN迭代30次时识别率约达98.58%并收敛.
综上可知,由于“跨层”连接的引入,C-DBN比DBN能更快地趋于收敛状态,并获得更好地识别性能.因此,采用文中设计的“跨层”连接方式可以有效提升DBN的性能.
3.3 主、次线耦合比例对网络性能的影响
在网络训练过程中,笔者发现主、次线的耦合比例(p∶q)对网络的识别率有显著的影响.下面,利用ASL数据集和MNIST数据集,采用3.2节所设参数,以p+q=1 为约束条件,以0.1为间隔,分析不同耦合比例对网络性能产生的影响.实验结果如图4所示.

图4 主、次线耦合比例对网络性能的影响
由图4可知,主、次线比例的不同对网络的性能具有明显的影响.在ASL数据集上,主线比例低于次线比例时,网络性能整体较好,在(0.1∶0.9)时识别率最高;在MNIST数据集上,识别率随着次线增加呈波动状态,并在(0.1∶0.9)时达到最高.因此,后续对两个数据集的实验中,主、次线比例均设置为 (p∶q)= (0.1∶0.9).
3.4 图像识别结果
为测试文中方法的有效性,增加了C-DBN与经典的深度网络模型LeNet-5和栈式降噪自编码(Stacked Denoising Auto-Encoder,SDAE)在ASL和MNIST数据集上的对比实验.具体对比算法包括:简化LeNet-5模型:含两个卷积层和两个降采样层,卷积核个数分别为6和12;SDAE:各隐含层节点数分别为600、200和100,学习率为0.5,并采用系数为 0.000 01 的L2范数正则;DBN:网络结构、学习率和正则项与SDAE相同;C-DBN:网络结构和正则项与SDAE相同,学习率为0.1,主、次线耦合比例为(0.1∶0.9).上述网络模型在ASL数据集上均迭代200次,在MNIST数据集上均迭代30次.此外,针对ASL数据集,加入了具有最好识别效果的SAE-PCA方法[14]; 对于MNIST数据集,加入了具有最好识别率的MCDNN方法[15].对比实验结果如表1所示.

表1 不同网络模型在两个数据集上的识别实验结果对比
表1显示,C-DBN在两个数据集上均获得了比较好的识别性能.其中,在ASL数据集上,相比于识别率最高的SAE-PCA,文中方法识别率降低约2%; 在MNIST数据集上,文中方法相比于最好的识别方法MCDNN降低约1.2%.然而,由于C-DBN仅利用单一的深度信念网络完成图像识别任务,并不包含基于传统方法的处理手段(如SAE-PCA),也没有采用基于多网络组合的策略(如MCDNN),因此,文中提出的基于C-DBN模型的方法识别性能是较优的.
4 结 束 语
笔者在深度信念网络结构的基础上,通过引入“跨层”连接,设计了一种耦合深度信念网络的图像识别方法.同时,以5层网络结构为例,文中在ASL数据集和MNIST数据集上对比分析了C-DBN和DBN的网络性能,验证了“跨层”连接在网络结构设计中的有效性,并讨论了不同主、次线耦合比例对网络性能的影响.实验结果表明,通过引入“跨层”连接可有效缓解梯度消失问题;同时,文中提出的C-DBN在收敛速度和识别性能上均优于相同网络层数下的DBN.此外,通过与经典的深度网络在ASL和MNIST两个数据上识别结果进行对比,说明C-DBN具有较强的学习能力和较好的图像识别性能.

