卡尔曼滤波在变形监测应用中的探讨
刘琼琼 张洪胜
(周口市规划建筑勘测设计院,河南 周口 466000)
20世纪60年代,美籍匈牙利数学家卡尔曼首先提出了用一个状态方程和一个量测方程来完整描述线性动态方程,即卡尔曼滤波方程,采用时域法及状态方程为其数学工具,以多变量控制、最优控制与估计以及自适应为主要内容。这是一种动态进行实时数据处理的有效方法,无需存储不同时刻的观测数据。在实际应用中,如何选择滤波模型,选择滤波初值、精度评定,本文将进行介绍,并结合应用实例说明。
1 卡尔曼滤波基本原理
卡尔曼滤波属于软件滤波方法,是以最小均方误差为最佳估计准则,采用信号与噪声的状态空间模型,利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计,求出当前时刻的估计值,根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误差的估计[1]。最初的卡尔曼滤波算法适用于解决随机线性离散系统的状态或参数估计问题。
在实际应用中,可以将物理系统的运行过程看成一个状态转换过程,卡尔曼滤波将状态空间理论引入物理系统的数学建模中,其假设系统状态可以用n维空间的一个向量X∈Rn来表示。为了描述方便,可以作以下假设:物理系统的状态转换过程,描述为一个离散时间的随机过程。系统状态受控制输入影响;系统状态及观测过程受噪声影响;对系统状态是非直接可观测的[2]。在假设前提下,定义系统状态变量为X∈Rn,系统控制输入为UK,系统过程激励噪声为WK,得出系统的状态随机差分方程:

定义观测变量Zk∈Rm,观测噪声为Vk,得到量测方程::

假设Wk、Vk为相互独立,正态分布的白色噪声,过程激励噪声协方差矩阵为Q,观测噪声协方差矩阵为R。A、B、H统称为状态变换矩阵,是状态变换过程中的调整系数,是从建立的系统数学模型中导出来的,假设它们是常数,得出卡尔曼滤波迭代的五个公式如下:
时间更新方程:

状态更新方程:
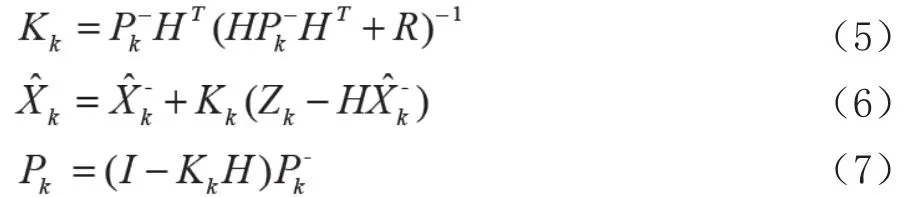
式中, A是作用在Xk-1上面的n×n状态变换矩阵;B是作用在控制向量Uk-1上的n×1输入控制矩阵;H是m×n观测模型矩阵,把真实状态空间映射成观测空间;为n×n先验估计误差协方差矩阵;Pk为n×n后验估计误差协方差矩阵;Q是n×n过程噪声协方差矩阵;R是m×m过程噪声协方差矩阵;I是n×n阶单位矩阵;Kk是n×m阶矩阵,称为卡尔曼增益或混合因数,可使后验估计误差协方差最小。
上述给出的是离散卡尔曼滤波的时间更新方程和状态更新方程(-代表先验,代表估计)。卡尔曼滤波主要分两步进行,先预测后修正,对应两个方程,预测方程(1)和修正方程(2)。预测方程功能:由系统上一状态最优估计状态推算出系统当前状态,即当前状态预测值=系统状态转移系数(A)×系统上一状态的最优估计值+状态估计噪声。修正方程功能:由系统当前状态的预测状态和实际观测值求取当前状态的最优估计状态,即系统当前状态的最优值=当前状态预测值+修正系数(K)×(实际观测量-当前状态预测值)。这个过程是预估-校正过程,对应的这种估计称为预估-校正算法。
2 滤波模型的选择
卡尔曼滤波模型误差的影响是卡尔曼滤波发散的重要原因之一。为了避免模型误差造成的不良影响,测量工作者要严格按照规定进行观测,保证观测过程的合理性和准确性,尽量给出接近实际的模型[3]。
在变形测量实时监测项目中,常用的卡尔曼滤波模型为位置、速度模型和位置、速度、加速度模型,这些是将监测点的变形位移看成一个随机过程。位置速度滤波模型认为在变形测量中,监测点位移速度的均值不变,在滤波中将监测点的位置、移速度作为状态量,将位移加速度视作动态噪声,其状态方程为:

位置、速度、加速度滤波模型认为在变形测量中,监测点位移加速度的均值不变,滤波中将监测点的位置、移速度和加速度都作为状态量,将加速度变化率视作动态噪声,,其状态方程为:

式中 xk、、分别为监测点的坐标、位移速度和加速度,Ωk-1为动态噪声,t表示时间。
观测噪声通过模拟观测实验获得。取若干期监测数据,计算监测点各期坐标及对应的速度、加速度,对速度和加速度作图分析。当各期速度在其平均速度的两侧波动变化,无明显增、减速迹象时,采用位置、速度模型;当各期速度有增、减速迹象,而其加速度无明显增、减速迹象时,采用位置、速度、加速度模型,最后根据各期加速度的变化率估算状态方程的动态噪声的方差。
3 模型精度的评定
当精确已知观测噪声和动态噪声的随机模型时,不需要专门进行精度评定,但实际应用中,所采用的先验系统状态误差协方差阵Q和量测误差协方差阵R与其实际值可能不完全一致,这时Q和R的含义与其说是协方差矩阵不如说是权逆矩阵更适当,式(7)中的Pk就是系统状态量的权逆矩阵,因此要计算单位权方差的估计值,以获得状态参数估计的协方差矩阵[4]。
对于第k期滤波,单位权方差σ2,可按照下式估计:
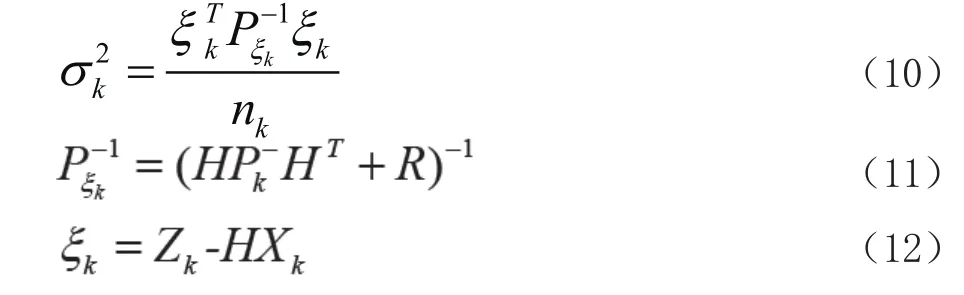
式中,nk为第k期滤波观测值的个数,为ξk预测残差向量的权逆矩阵,这时状态参数向量滤波值得协方差:

在施工变形测量中,nk往往较小,这时按式(10)求得的可能不稳定。理想方法是通过平滑的各期状态参数向量的平滑值,根据平滑后的残差向量来估计,但平滑计算较复杂,计算量也很大。为了化简计算,同时消除值的不稳定性,可将式(10)计算的各期值,按权(各期观测值的个数)取平均值近似地计算的估值,若以Nk表示第k期以前(包括第k期)各期观测个数之和,Wk表示第k期以前(包括第k期)各期之和,经推导可得下列公式:

用卡尔曼滤波法处理数据的一般步骤是:首先,获取部分对象的监测数据来确定系统状态量模型。其次,提取建立卡尔曼滤波模型所需的预测噪声量和量测噪声量,确定系统状态量初值。再次,建立系统卡尔曼滤波模型,处理观测数据[5]。其中,根据对监测数据的分析选择合适模型,提取相应的预测噪声量和量测噪声量是关键,需要根据具体工程数据分析获得。
4 应用实例
以滨州大桥运行监测项目为例。获得采用动态RTK模式解算的大桥监测三维坐标数据,经过统计分析,此处采用位置、速度、加速度模型,设t为监测周期,设某时刻观测点的位置为Xk,其瞬时速率为,瞬时加速度为,将加速度的瞬时变化看作随机干扰(动态噪声)。记此点的状态向量为:为9×1的矩阵,I为3×3的单位阵,系统状态方程为:

可得系统状态方程:

Lk+1为3×1观测值矩阵,Bk+1为3×9观测模型矩阵,为观测噪声,可得卡尔曼滤波迭代的五个公式:

三维坐标数据处理采用卡尔曼滤波处理结果(如图1所示),绿色曲线为滤波后结果,红色曲线为实测数据,滤波效果明显,数据波动符合实际监控情况。

图1 观测数据滤波效果
滤波数据单位权中误差会发生变化,滤波值的中误差越来越小,精度逐步提高,趋于稳定值。有关结果如表1所示(这里仅列出10组数据)。
由表1看出,监测值与滤波值之间残差的最大值为-4.588mm,最小值为0.377mm,残差有正有负,有很强的随机性,预测误差为1.08cm,对采用动态RTK模式解算数据而言,预测效果较好。

表1 变形监测值与相应的滤波值
5 结束语
本文详细探讨了卡尔曼滤波在监测应用中如滤波模型的选择,模型初值的设定和精度评价方法,并结合具体的工程实例,论证了该方法在动态变形监测中的可行性,滤波解算结果具有较高的精度。卡尔曼滤波适合估计线性随机差分方程描述的随机过程的状态变量,在变形监测工程领域有广泛的应用前景。

