基于复合重复控制的LCL型三相四开关有源电力滤波器

张 帅，郭源博，张晓华

（大连理工大学电气工程学院，大连116024）

20世纪80年代以来，电力电子技术飞速发展，各种电力电子装置得到了越来越广泛的应用，这些非线性负载使得电网谐波含量不断上升。有源电力滤波器APF（active power filter）作为一种动态、灵活的谐波治理手段，得到了广泛的研究与应用，尤其在APF的稳定性与可靠性运行方面，近年来受到了更多的关注[1-3]。三相四开关有源电力滤波器TF-APF（three-phase four-switch active power filter）作为三相六开关APF的容错拓扑，能够在容错状态下实现与三相六开关APF相同的功能[4]，相关研究对于APF的稳定可靠运行有着重要的意义。文献[5]叙述了TF-APF的拓扑结构与原理，并提出了直流电容电压控制方法和指令电流调制方法；文献[6]提出了一种针对TF-APF的滞环控制方法，具有开关损耗小、可靠性高的优点；文献[7]提出了一种新型的指令电流确定方法，适用于TF-APF电网电压不平衡和电网短时故障时指令电流的确定；文献[8]研究了TF-APF的空间矢量脉宽调制SVPWM（space vector pulse width modulation）算法；文献[9]以网侧电流作为TF-APF的电流检测和控制目标，简化电路，降低成本。由此可见，目前对于TF-APF的研究主要集中于普通TF-APF在容错拓扑结构、直流侧稳压、调制策略及控制算法等方面，对于采用LCL输出滤波器的TF-APF的研究并未引起足够重视。LCL输出滤波器相比于传统的L和LC输出滤波器，具有体积更小、高频衰减性能更好、动态响应速度更快等优点，能够进一步提高TF-APF的补偿精度[10]。

然而，LCL型输出滤波器存在谐振尖峰，对系统稳定性十分不利。传统的无源阻尼谐振抑制方法存在阻尼损耗过高、系统发热、开关频率滤波效果受限等缺点。因此，有学者提出了采用电容电流反馈的有源阻尼方法来抑制谐振峰。但是目前的研究主要针对LCL型六开关APF拓扑，且此时控制方法一般为单纯PI控制，对于LCL型四开关容错APF的复合重复控制与电容电流反馈控制研究尚未引起足够重视[11-13]。本文针对LCL型TF-APF系统，设计复合重复控制器，并采用改进电容电流反馈的控制方法有效抑制了谐振峰，具有无阻尼损耗和不影响高频滤波特性的优点，可提高系统的稳定性与可靠性。

重复控制基于内模原理，近年来在三相六开关APF上得到了较多的应用[14]。虽然重复控制具有无静差跟踪周期性给定信号的优点，但逐周期累加控制的特性使其同时具有响应速度慢的缺点[15]。因此，本文在TF-APF容错控制系统设计中，采用将重复控制与PI控制相结合的复合控制策略，兼顾了高稳态精度和快速动态响应的优点，取得了令人满意的效果。

1 系统建模

1.1 abc坐标系下模型

LCL型TF-APF的拓扑结构如图1所示，其主电路中2个串联的电容器容值完全相同，电压相等，令Cd1=Cd2=C，ucd1=ucd2。因电网中三相电流电压对称，所以三相电压usa+usb+usc=0，三相电流ica+icb+icc=0。电容支路上可通过串联电阻来抑制LCL型3阶系统的谐振峰值。

定义b、c相开关管对应的开关函数为

因为LCL输出滤波器用于滤除APF输出的高频开关次谐波，流过的基波电流很小，所以建模时可忽略RC支路影响，令L1+Ls1=L2+Ls2=L3+Ls3=L。

根据基尔霍夫电压定律，可得到LCL型TFAPF在abc坐标系下模型的状态方程，即

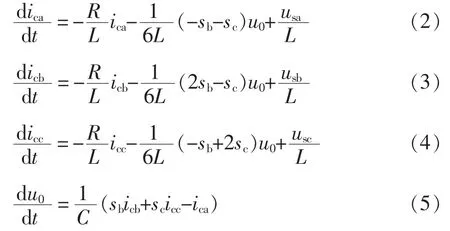
图1 LCL型三相四开关有源电力滤波器的拓扑结构Fig.1 Topological structure of TF-APF with LCL-filter

式中：u0为直流侧总电压，u0=ucd1+ucd2；usa、usb、usc为网侧电压；uca、ucb、ucc和 ica、icb、icc分别为 APF 的输出电压和电流；R为电感的等效电阻。由式（2）～式（5）可知，通过控制开关组合函数（sb、sc）便可控制APF输出的补偿电流和直流侧电压。

1.2 dq坐标系下模型

令 us=[usausbusc]T，ic=[icaicbicc]T，则 abc 坐标系下式（2）～式（4）用向量形式表示为

Park 变换可以将三相静止坐标系（a，b，c）转换到两相同步旋转坐标系（d，q，0），有多种形式。本文选用的变换矩阵为

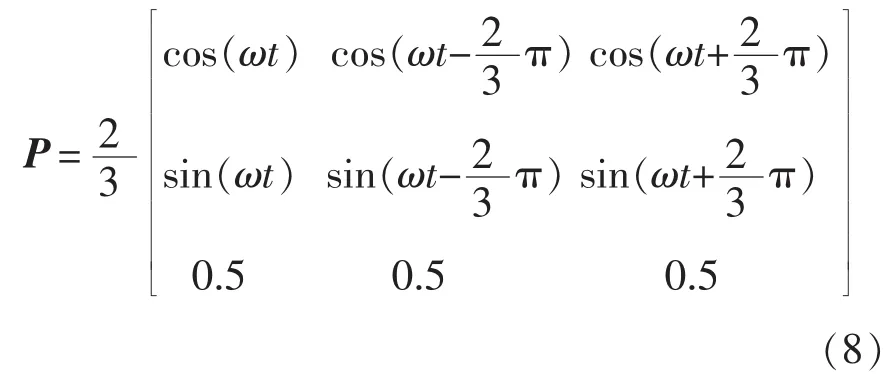
为了描述TF-APF在dq坐标系下的模型，采用了一种简化Park变换，即P矩阵的一个子阵，形式为

将式（6）进行 Park 变换，即

对开关函数sb、sc用简化Park变换矩阵Pu，即

式（10）中各项做相应简化，得

将式（12）～式（14）代入式（10）中，得到 TF-APF在dq坐标系的模型，即

2 LCL输出滤波器及其控制策略

2.1 LCL输出滤波器原理

LCL型输出滤波器的等效电路如图2所示。

图2 LCL型输出滤波器等效电路Fig.2 Equivalent circuit of LCL-filter

由于L1和L2的等效内阻较小，在此忽略。RC为电容C支路的串联电阻。i1为L1支路电流，i2为L2支路电流。udc为逆变器直流侧电压，ui为逆变器输出电压，us为电网侧电压。XL1为L1支路阻抗，XL2为L2支路阻抗，XC为C支路阻抗。

逆变桥侧电流为

根据式（18）～式（20）可求得逆变器输出电压Ui到补偿输出电流 I2（s）的传递函数 G（s）为

令L=L1+L2，由式（21）可知，当串联的无源阻尼电阻RC=0 Ω时，LCL型输出滤波器与单电感L型输出滤波器的频率特性如图3所示。

图3 LCL和单电感L的频率特性Fig.3 Frequency characteristics of LCL and single L

从频率特性对比可以看出，总电感量相同的L和LCL滤波器在谐振频率点前的低频段，两者的频率特性相同；而在谐振频率点以后的高频段，LCL滤波器的衰减率为-60 dB/dec，远小于L滤波器的-20 dB/dec。因此LCL滤波器拥有更好的滤除开关次谐波的能力。但是，LCL滤波器作为3阶系统，在谐振频率点处存在谐振尖峰，严重影响补偿精度与系统稳定性，因此需抑制谐振尖峰。

2.2 一种基于电容电流反馈的谐振峰抑制策略

传统的无源阻尼抑制方法如在电容支路串联阻尼电阻，具有实现简单，不受开关频率限制等优点，得到广泛的应用。但无源阻尼方法存在两个缺点：一是存在阻尼损耗巨大、发热等问题；二是，随着阻尼电阻的增大，LCL滤波器的高频衰减特型逐渐变差，如图4所示。

基于以上分析，为了解决无源阻尼存在的上述问题，本文采用一种基于电容电流反馈控制的方法，其策略如图5所示。从电容支路引入负反馈电流，经过比例增益H1后接入复合重复控制器的输入端，再经过复合重复控制器的控制便能够有效抑制谐振峰。

因为引入电容电流反馈后，未使用阻尼电阻，不存在因阻尼电阻而造成的大功率损耗。与此同时，LCL输出滤波器的硬件结构未改变，引入反馈后不会影响高频衰减特性。

图4 采用不同阻值无源阻尼时LCL滤波器频率特性Fig.4 Frequency characteristics of LCL-filter for passive damping with different resistances

图5 电容电流反馈控制策略Fig.5 Capacitor current feedback control strategy

3 复合重复控制器

3.1 重复控制原理分析

内模原理指出：在控制器内植入一个与指令信号同频的正弦信号，便可以对正弦指令信号无静差跟踪。所以控制内模Gm（s）可为频率ωn的正弦信号提供无穷大的增益，即

由于TF-APF中指令信号各谐波频率都是基波信号的整数倍，所以应将控制器内模设计为

因TF-APF需要补偿的电流谐波次数较多，式（23）所示内模设计过于复杂，所以可以采用如下形式的重复信号发生器内模

式中，T为基波周期。该内模是一个基波周期延迟正反馈环节，TF-APF指令信号中所有成分经过该内模后均被复制而重复出现，该环节相当于一个以周期为步长的积分控制器。

重复控制有N个极点位于单位圆上 （N为每基波周期采样点数）。整个系统处于临界稳定状态，系统稳定性不佳。因此可在重复控制正反馈环节的前向通道上串联一个低通滤波器，通常为一个略小于1的常数。改进的重复控制信号发生器如图6所示。

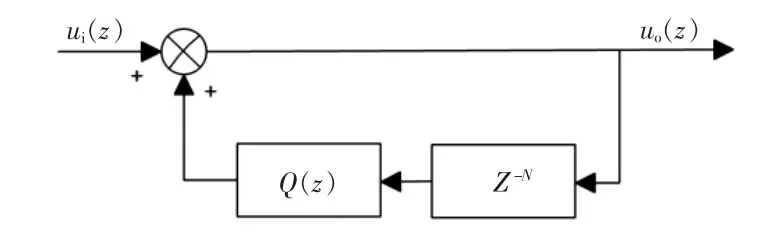
图6 改进重复控制信号发生器的离散化模型Fig.6 Discrete model of signal generator under improved repetitive control

其传递函数为

将式（25）写成差分方程的形式，取 Q（z）=0.95，则第k次输出为

式（26）表明，重复控制内模仍然是以一个基波周期为步长进行累加。但是上一个基波周期的控制量衰减了5%，呈收敛状态，避免了重复控制器积分饱和。

3.2 复合重复控制器设计

根据以上分析，设计重复控制器整体结构，如图7所示。重复控制器由改进重复信号发生器和补偿器 C（z）组成。C（z）针对被控对象 G（z）设计，用来补偿幅值和相位偏差，对系统稳定性有重要作用。

从重复控制原理分析中可以看出，重复控制逐周期对各频次正弦信号进行累加，逐周期修正。当系统刚投入使用或负载参数突变时响应速度较慢，会影响补偿效果。因此本文采用将响应速度快的PI控制与跟踪精度高的重复控制复合的控制方法，其结构如图8所示。

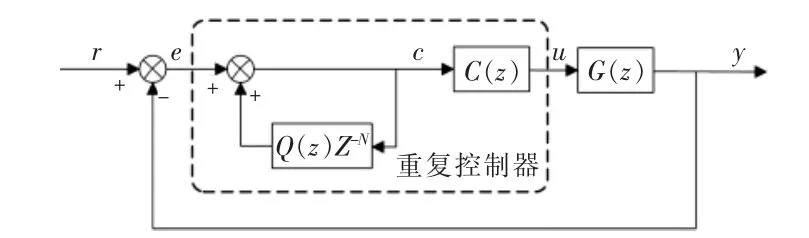
图7 纯重复控制器结构框图Fig.7 Block diagram of simple repetitive controller

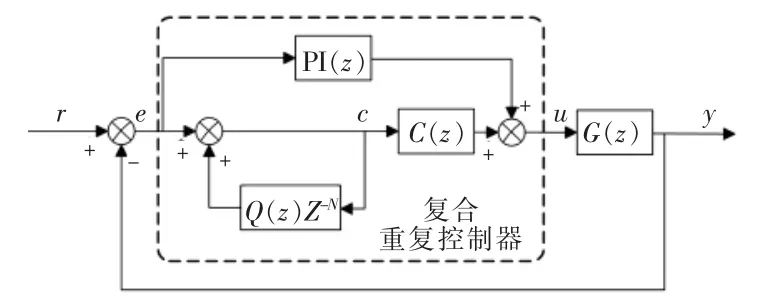
图8 复合重复控制器结构框图Fig.8 Block diagram of hybrid repetitive controller

4 仿真验证

为了验证所提出的整体设计方案的有效性，本文在Matlab平台上进行仿真分析。网侧相电压为220 V/50 Hz，对于三相六开关APF，直流侧电压给定值通常大于网侧相电压峰值的2倍，取800 V。但TF-APF的直流电压利用率仅为同条件下三相六开关APF的一半。因此，本实验TF-APF直流侧电压给定值为1 600 V。系统其他参数为：开关频率10 kHz；LCL输出滤波器逆变器侧电感L1=L2=L3=4 mH，网侧电感Ls1=Ls2=Ls3=0.5 mH，滤波电容C1=C2=C3=4 μF，电容等效电阻 R1=R2=R3=0.05 Ω。LCL 滤波器的谐振峰频率为

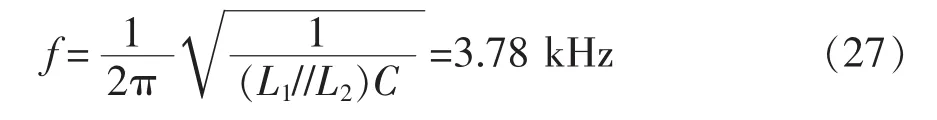
首先进行基于复合控制的LCL型TF-APF的仿真，结果如图9所示。当TF-APF稳定运行时，负载侧电流波形有较大畸变，THD达到18.02%。经过TF-APF补偿后，电网电流波形接近标准正弦波，并且THD下降到2.28%，补偿效果显著。从FFT分析中可以看出，低次谐波在复合控制的作用下得到有效的补偿，10 kHz的高频开关次谐波被LCL型输出滤波器有效滤除，而LCL型输出滤波器所产生的谐振峰通过改进型电容电流反馈有源阻尼控制策略得到了大幅抑制。

其他条件与图9实验相同的情况下，用传统的PI控制策略替代复合重复控制的TF-APF的实验结果，如图10所示。

图9 基于复合重复控制的LCL型TF-APF仿真结果Fig.9 Simulation results of TF-APF with LCL-filterbased on hybrid repetitive control

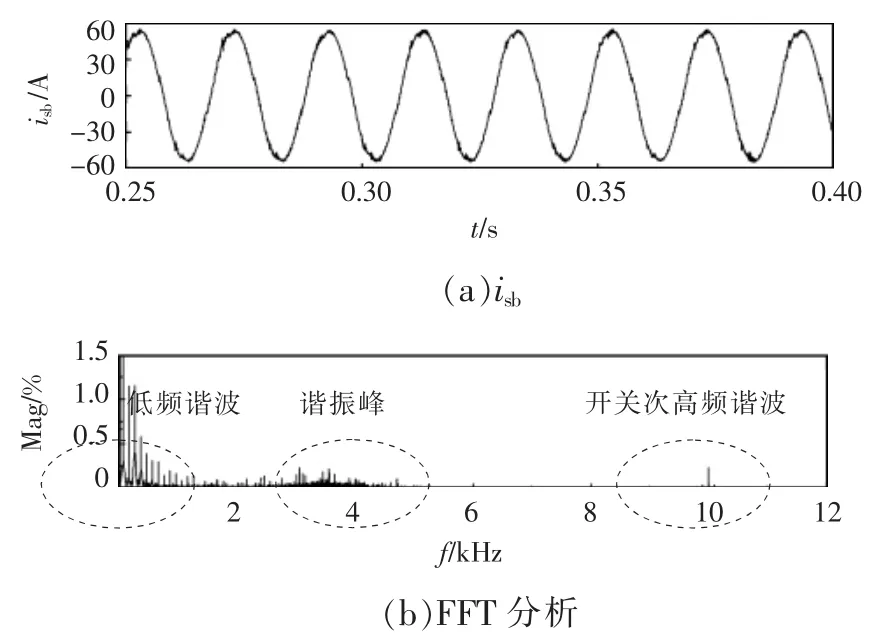
图10 基于PI控制的LCL型TF-APF仿真结果Fig.10 Simulation results of TF-APF with LCL-filter based on PI control

经过TF-APF补偿后，电网电流总谐波畸变率为3.89%。从补偿后的电网电流波形可以看出，电流在波峰波谷处存在较大畸变。从FFT分析中可以看出，相比于复合重复控制策略，传统的PI控制在低频处，谐振峰处和10 kHz开关频率的高频处谐波含量均较大，总THD较大。在本实验条件下为了达到好的跟踪效果，P参数选取过大，对系统稳定性不利。

其他条件与图9实验相同的情况下，用纯重复控制替换复合重复控制的TF-APF的实验结果，如图11所示。

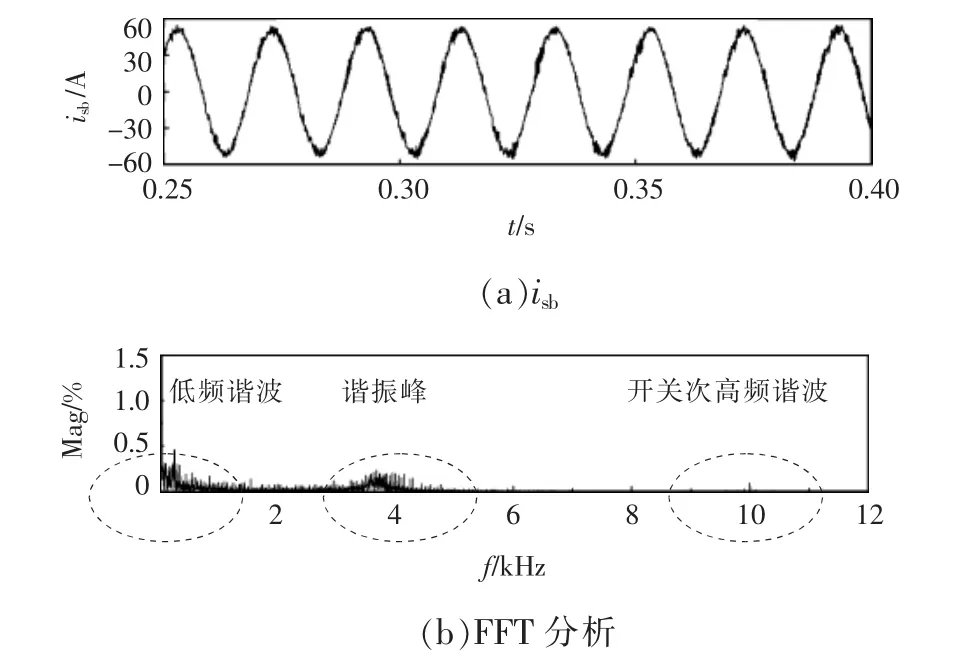
图11 基于纯重复控制的LCL型TF-APF仿真结果Fig.11 Simulation results of TF-APF with LCL-filter based on simple repetitive control

经过TF-APF补偿后，电网电流总谐波畸变率为2.32%。从补偿后的电网电流波形及FFT分析中可以看出，波形存在较大毛刺，这是由低次谐波和谐振尖峰处谐波含量较大所引起的。

其他条件与图9实验相同的情况下，用总电感值相同的L型输出滤波器替代LCL型输出滤波器的TF-APF的仿真结果如图12所示。

经过TF-APF补偿后，电网电流总谐波畸变率为3.19%。从补偿后的电网电流波形及FFT分析中可以看出，采用L型输出滤波器的TF-APF补偿后的电流中10 kHz开关次谐波依然很大，而采用LCL型输出滤波器则大幅降低开关次谐波。LCL型输出滤波器对开关次谐波的抑制能力远高于L型输出滤波器。虽然存在谐振峰，但有源阻尼控制策略有效抑制住谐振峰的影响。总的来看采用有源阻尼的LCL输出滤波器滤波效果更佳。

图13和图14为其他条件与图9实验相同的情况下，分别采用纯重复控制和复合重复控制，在0.02 s时投入LCL型TF-APF的网侧电流仿真结果，以观察两种控制方法的动态性能。

图12 基于复合重复控制的L型TF-APF仿真结果Fig.12 Simulation results of TF-APF with L-filter based on hybrid repetitive control

从图13、图14中可以看出，纯重复控制TFAPF在0.02 s投入使用后，补偿后的电网电流波形经过较长时间才稳定下来，逐渐接近正弦波。而采用复合重复控制的TF-APF在0.02 s投入使用后，波形迅速稳定下来，兼具了PI控制的快速响应特点。

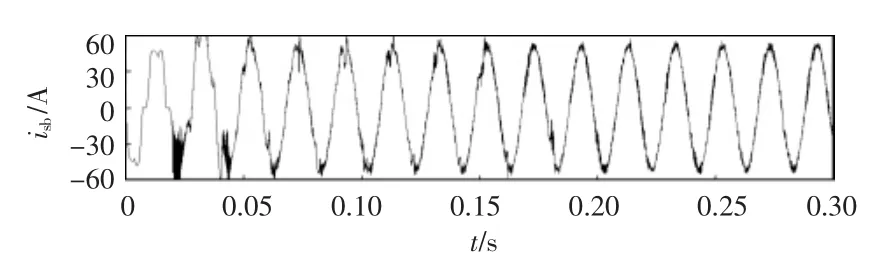
图13 基于纯重复控制的LCL型TF-APF动态性能Fig.13 Dynamic performance of TF-APF with LCL-filter based on simple repetitive control

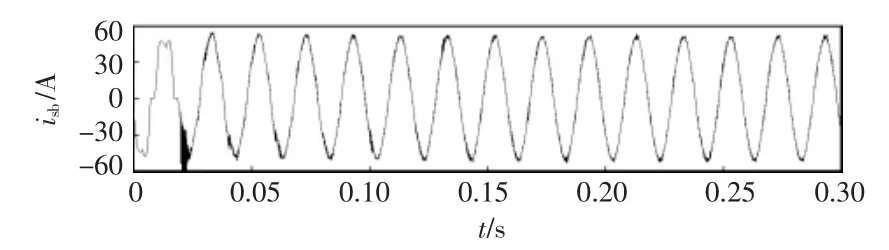
图14 基于复合重复控制的LCL型TF-APF动态性能Fig.14 Dynamic performance of TF-PF with LCL-filterbased on hybrid repetitive control

5 结语

LCL型三相四开关有源电力滤波器能够在容错的状况下实现对谐波的有效补偿，提高了系统运行的稳定性与可靠性。本文针对LCL型TF-APF存在谐振峰的问题，通过采用一种电容电流反馈控制方法，有效抑制谐振峰同时，避免阻尼损耗和高频衰减特性变差等问题，提高了稳定性和可靠性。通过对复合重复控制器的合理设计，使得复合重复控制器能够高精度快速地跟踪指令电流信号。相比于PI控制和纯重复控制，复合重复控制对LCL型TFAPF的控制效果更佳，提高了LCL型TF-APF的补偿精度。仿真实验验证了基于本文设计的LCL型TF-APF的可行性和有效性。