自适应多层复形遗传算法在钛合金动态本构模型参数识别中的应用

盛 鹰， 曾祥国， 陈国平， 刘筱玲， 文 军

(1.西南科技大学 土木工程与建筑学院， 四川 绵阳 621000； 2.四川大学 建筑与环境学院， 四川 成都 610065)

0 引 言

钛合金因具有密度小、比强度高、耐高低温、耐腐蚀等综合性能，而被广泛运用于航空航天、生物医疗等领域[1-2].与其他金属材料不同的是，钛合金材料对应变率和温度非常敏度，在高应变率、高温环境下表现出与中应变率、常温环境下截然不同的力学性能[3].为准确描述钛合金材料与不同应变率、不同温度相关的力学行为，学者们提出了多种本构模型，如Johnson-Cook模型、Khan-Huang-Liang模型、Chaboche模型等[4-6].其中，Johnson-Cook模型是一种常用的经验型本构模型，其形式简单，各参数具有清晰、明确的宏观物理含义，参数个数较少，能较好地模拟多种常用工程材料的动态本构行为，能广泛用于工程结构或重要构件在动态载荷作用下的动力学模拟分析.此外，针对钛合金在高应变率下表现出的热粘塑性，学者们验证了Johnson-Cook模型能很好地拟合钛合金在低应变率和中应变率下的动态拉压行为，但却不能方便地描述其在高应变率下的应力—应变关系[7-8].为使Johnson-Cook模型能广泛适用于描述钛合金在不同应变率、不同温度下的应力—应变关系，本研究在Johnson-Cook模型基本形式不变的情况下，重新定义了温度项的物理意义和表达形式，得到了修正的广义Johnson-Cook模型，可很好地解决了这一问题.但广义Johnson-Cook模型中含有6个需要通过大量实验数据来拟合确定的待定参数.为降低参数识别的计算工作量，提高参数识别的效率和精度，本研究在遗传算法[9]和复形法[10]的基础上，提出了一种自适应多层复形遗传算法，其能显著提高参数识别的效率和精度，并以Ti-6Al-4V钛合金为算例，描述了其在不同应变率、温度下的单轴流变应力—塑性应变曲线，数值模拟结果和已有的试验数据吻合良好.

1 钛合金Johnson-Cook动态本构模型

1.1 经典Johnson-Cook模型

经典Johnson-Cook模型是一种常用的经验型本构模型，其流变应力—塑性应变关系表达式为，

(1)

(2)

1.2 Johnson-Cook模型温度项修正

(3)

式中，β为功热转换系数，ρ和Cp为材料密度和比热容，k为常系数.

Tt+1=Tt+(ΔT)t+1

(4)

因此，在经典Johnson-Cook模型的基础上，将温度项T修正为材料的瞬时实际温度，即考虑T为与时间t相关的量，则只需用式(4)的Tt+1代替式(1)的T，即可得到修正的广义Johnson-Cook模型，

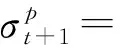
(5)

需要说明的是，在低应变率和中应变率下，多数金属材料的内部温度来不及升高就已经扩散，此时K≈0,修正广义Johnson-Cook模型就退化为了经典Johnson-Cook模型.因此，经典Johnson-Cook模型其实是该修正广义Johnson-Cook模型的一种特殊情况.

2 自适应多层复形遗传算法

2.1 多参数识别数学模型

本构参数识别的目的是寻找一组材料参数，使计算值与试验值之间的综合误差最小，如式(6)所示，

(6)

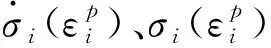
对此，本研究将采用自适应多层复形遗传算法进行本构参数识别，使目标函数(6)取到最小值.

2.2 自适应多层复形遗传算法

自适应多层复形遗传算法的基本步骤包括：形成初始复形，检验收敛条件，找到最坏点，调优搜索寻求改进点.如此反复进行，使复形逐渐缩小，逼近最优点，然后在最优点附近用遗传算法作局域精确搜索.其具体实现步骤如下：

1)采用随机试验法投点，形成初始复形.

首先对可能的范围作上、下界估计，以确定试验域和采用随机试验法投点.此处可能的初始投点范围不必包含各参数的最优解.

为了能有效控制随机数精度，采用random(num)函数产生1到num之间的随机整数，再取倒数则得到了0到1之间的随机数ζ.于是，各顶点的变量列阵可表达为，

(7)

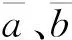
改进技巧包括：其一，首先产生一组随机数存放于数据文件中备用，为避免产生伪随机数，要通过比较和筛选确保产生的随机数不出现重复；其二，若产生的某个初始点不满足约束条件，则顺次读入下一个随机数构成新的初始点再进行判断，直到所有顶点全部可用为止.

2)对复形各顶点的目标函数值进行排序，检验收敛条件.

处理技巧为：第一层复形均以迭代次数作为停机准则，各个复形分别迭代5到10次则停止.但第二层复形则以式(8)作为终止迭代依据.若成立则终止迭代，反之进入“调优搜索"步进行再次迭代.

(8)

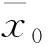
(9)

通过这种改进，一方面有效减少了结构分析次数，另一方面也找到了停止迭代的合理判据，确保终止迭代后的最好点接近全局最优点.当第一层复形迭代完成后，则初始化第二层复形.这里有一个改进技巧：传统的多层复形法仅从各复形中取出最好与次好点组成第二层复形，但如果各复形顶点较多，则选点个数不仅仅局限于最好与次好点.适当增加选点个数可有效减少优化分析次数，而不会对精度造成影响.

3)调优搜索阶段.

(10)

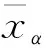
(11)

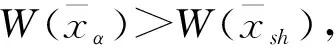
(12)

完成调优搜索过程后，则返回第3)步再次对新复形各顶点对应的目标函数排序和检验收敛条件.直到满足收敛条件(8)时，复形迭代终止.

其中，第3)步的调优搜索子程序流程图如图1所示.第1)～3)步程序设计流程图如图2所示.

图1 第3)步调优搜索子程序流程图

4)在最优点附近用遗传算法作局域精确搜索.

(13)

式中，γi为变量xi附近的搜索邻域.

然后对各变量在调整后的范围内，运用遗传算法[14]进行更精密的智能进化搜索，通过选择、交叉和变异运算，可获得精度更高的最优解.

第4)步遗传算法局域精确搜索的子程序流程图如图3所示.

图2第1)～3)步程序流程图

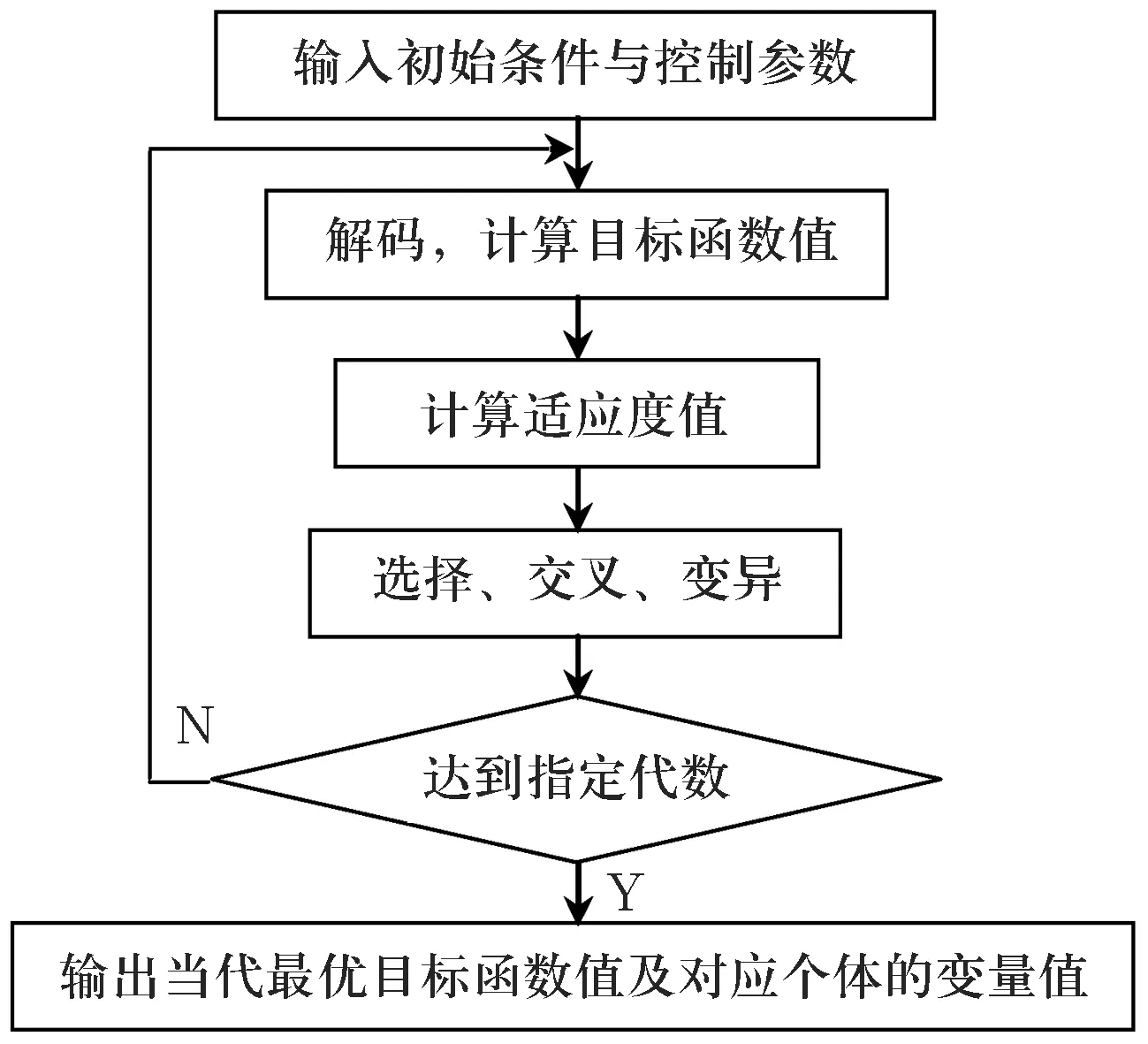
图3 第4)步遗传算法搜索子程序流程图

3 算例分析

本研究以Ti-6Al-4V钛合金(熔点温度Tm=1 933 K，弹性模量E=107 800 MPa)为例，采用准静态试验和动态加载试验获得的多种应变率、温度下的流变应力—塑性应变试验数据[7]，对本研究建立的修正的广义Johnson-Cook模型及待定参数的识别方法进行验证.

修正的广义Johnson-Cook模型中Ti-6Al-4V钛合金的各材料常数如表1所示.

表1 修正的广义Johnson-Cook模型中Ti-6Al-4V材料常数

将表1所得的各参数值代入式(5)的本构模型中即可得到不同应变率、不同温度下钛合金的流变应力—塑性应变关系.在不同低应变率、不同温度下， Ti-6Al-4V钛合金的流变应力—塑性应变的试验数据和计算结果比较如图4所示；在不同高应变率、不同温度下，Ti-6Al-4V钛合金的流变应力—塑性应变的试验数据和计算结果比较如图5所示.

图4不同低应变率、不同温度下Ti-6al-4V的应力—应变曲线的试验和计算比较

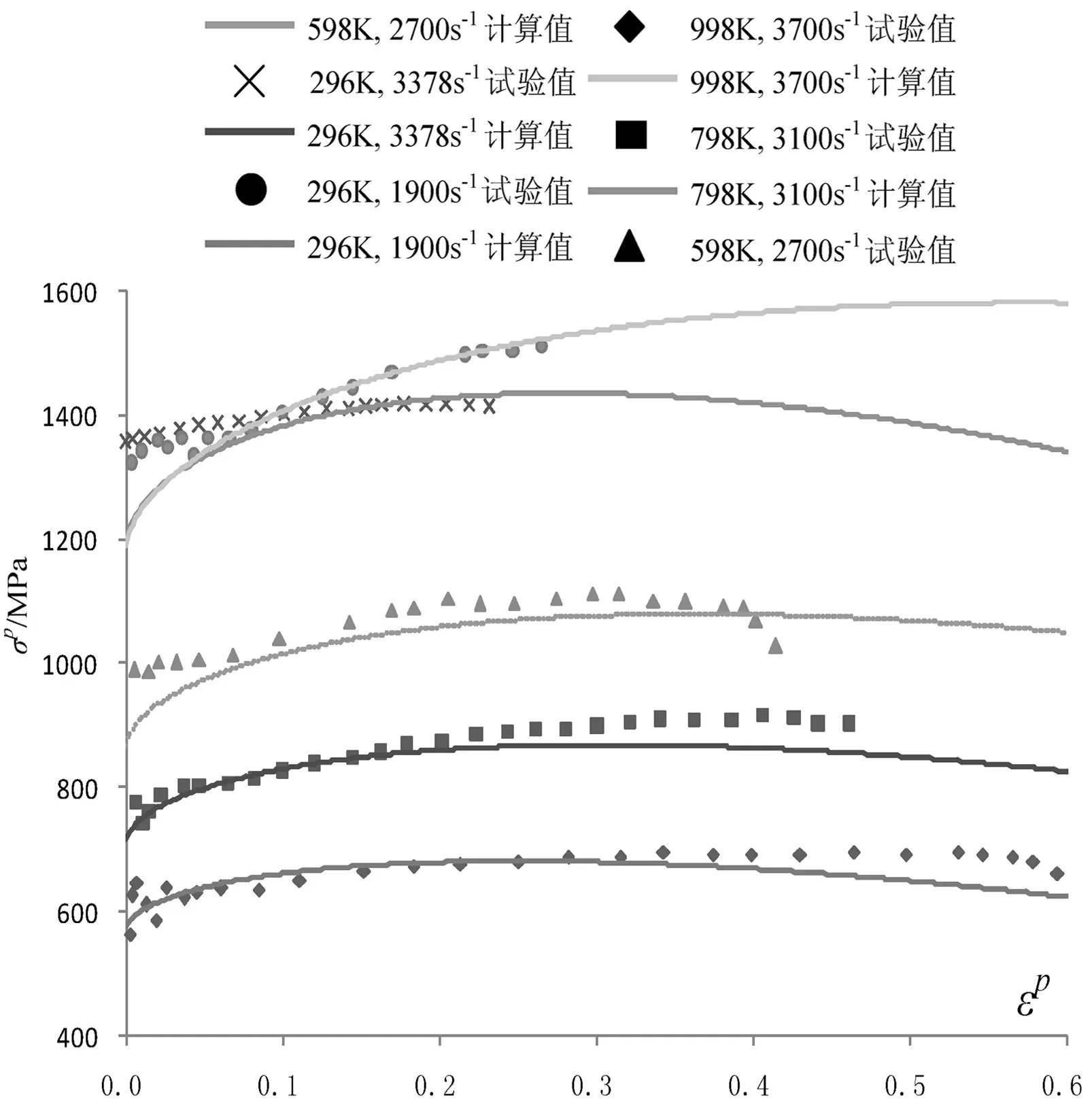
图5 不同高应变率、不同温度下Ti-6al-4V的应力—应变曲线的试验和计算比较

由图4和图5可知，计算结果与试验数据吻合良好.此验证了本文提出的修正广义Johnson-Cook模型与自适应多层复形遗传算法的可靠性.

需说明的是，表1中拟合得到的6个Ti-6Al-4V材料常数是运用图5中5组不同的高应变率、不同温度下的试验数据获得的，再将求出的待定参数代入修正广义Johnson-Cook模型中，进而可获得6组不同低应变率、不同温度下的拟合曲线.由图4可知，这些拟合曲线与不同低应变率、不同温度下的试验值吻合仍较好.此表明该修正广义Johnson-Cook模型对Ti-6Al-4V材料的本构关系具有较好的预测性.

4 结 论

钛合金是应变率敏感材料，在中应变率及以下的加载条件下，在相同的温度下，应变率越高，给定应变下的流变应力也越高.在高应变率下，钛合金表现出热粘塑性，由于加载速度很快，钛合金内部温度迅速升高且来不及扩散，将降低应变、应变率的强化作用，使流变应力呈下降趋势.本研究提出的修正的广义Johnson-Cook模型能较好地拟合钛合金在不同应变率(低应变率、中应变率、高应变率)、不同温度(常温、高温)下的本构关系.本研究提出的自适应多层复形遗传算法有效克服了复形法、遗传算法存在的无法同时满足精度、可靠性和计算时间3方面的要求，且方法无需预先估计各待定参数最优解所在的取值范围，显著提高了对最优解的全局搜索能力，能快速、精确、可靠地实现优化问题的求解.此外，本研究提出的确定材料本构关系材料常数的自适应多层复形遗传算法对其他工程材料高精度本构关系的建立具有重要参考价值.