基于红外光谱的沥青SBS含量自动测定方法

陈志国, 秦卫军, 卓 瑞, 田 冰, 钟 涛

(1. 吉林省交通科技研究所 科技成果转化中心, 长春 130022； 2. 吉林大学 交通学院, 长春 130022)

0 引 言

沥青路面作为我国公路的主要形式, 具有路面平整、 水稳定性高、 噪音低、 养护容易等特点, 但由于沥青路面存在高温易软化, 低温易断裂等缺点, 降低了沥青道路的使用寿命。我国幅员辽阔, 气候多样性, 沥青路面的缺陷严重影响了道路使用寿命。为改善沥青路面的性能, 各种聚合物改性沥青取代传统沥青被应用于道路施工, 其中SBS(Styrene-Butadiene-Styrene copolymer)改性沥青, 苯乙烯-丁二烯-苯乙烯三嵌段共聚物)尤为常见[1-4]。

SBS改性沥青是在基质沥青基础上添加SBS改性剂, 混熔之后, 形成稳定网络结构的聚合物沥青。该改性沥青具有粘结力强、 高低温稳定性好、 耐老化性强等优点, 但SBS含量的不同直接影响了SBS改性沥青的性能, 决定了道路使用寿命[5]。为满足不同地区、 道路等级、 气候等道路的内在要求, 确立了道路施工SBS改性沥青含量的技术标准。为确保道路施工质量, SBS改性沥青的SBS含量监管尤为重要。

目前国内外已有不少学者对关于沥青SBS改性剂含量测定方面做了相关研究。林杰[6]采用荧光显微法, 得出不同含量SBS改性沥青内部形成的微观结构有所差异且各自具有不同特征的结论, 但该法仅能对SBS改性剂含量做出初步判断, 无法精准地测定SBS含量； 耿九光等[7]采用凝胶渗透色谱(GPC: Gel Permeation Chromatography)分析技术对不同SBS含量的改性沥青做了分析研究, 发现GPC测试数据与沥青SBS改性剂含量存在显著的线性关系, 最后建立GPC数值与沥青SBS含量标准曲线。但该方法原理是聚合物在分离柱上按分子流体力学体积大小被分离开, 存在方法复杂、 速度慢等缺点。高妮妮[8]利用红外光谱分析技术, 研究了特征峰处吸收度比值与沥青SBS含量关系, 提出了基于红外光谱法测定SBS含量方法； 孙大权等[9]同样基于红外光谱分析技术, 建立特征峰峰面积比与沥青SBS含量关系表达式。从上述研究所见, 目前SBS含量测定方法主要为实验测定法和红外光谱测定法, 其中实验测定法具有实验复杂、 实时性差等缺点, 难以应用于大型道路施工过程。红外光谱法虽然具有检测精度高、 操作简单等特性, 但红外光谱的独特优势主要利用红外光谱快速且直观表达出物质结构、 物质是否存在等方面信息, 而物质浓度等信息主要利用通用的红外光谱软件, 如OMNIC等, 人工分析获取, 这些制约了道路施工的应用需要。

针对目前缺乏快速一体化的SBS改性沥青含量检测的专用工具手段, 笔者利用红外光谱分析方法, 建立了一种SBS改性沥青含量测定方法。该方法利用红外光谱SBS测定原理, 获取改性沥青光谱原始测定数据, 引入复化辛普生面积计算方法, 计算红外光谱特征峰, 然后根据朗伯-比耳定律, 实验标定出标准曲线, 并对标准曲线进行校正和验证。结果表明该方法在继承红外光谱法速度快、 操作简单优良特性基础上, 弱化数据的获取依靠某些特定软件的缺陷、 缩短数据预处理过程, 且相对原有的梯形求积公式精度更高, 从而满足工程上速度快、 精度高、 易操作等要求。

1 红外光谱测定SBS含量原理

当一定波长的红外光照射样品时, 如果分子中的某个基团的振动频率和该红外光相同, 二者就会发生共振, 此时光的能量通过偶极矩的变化传递给分子, 这个基团就会吸收该频率的红外光而发生振动能级跃迁, 产生红外吸收峰。不同的物质基团具有不同的特征吸收峰, 当某基团是当前混合物中某物质所独有的, 则该基团对应的吸收峰就能成为分析该物质浓度的重要依据[10]。根据朗伯-比耳定律, 不同物质基团浓度与其特征吸收峰吸收强度具有正相关关系。因此, 可以根据不同的特征峰吸收强度预测其对应的物质基团的浓度。

朗伯-比耳定律描述为： 当一束光通过样品时, 任一波长光的吸收强度与样品中的各组成分的浓度成正比[11]。

(1)

其中A(ν)、T(ν)分别表示在波数(ν)处的吸光度和透射率；a(ν)表示在波数(ν)处的吸光度系数；b表示光程长(样品厚度)；c表示样品浓度。

吸光度A常用吸收峰峰高表示, 也可以用吸收峰峰面积表示。进行定量计算时, 使用吸收峰峰面积将比使用吸收峰峰高更准确些, 这是因为峰面积受样品因素和仪器因素的影响比峰高更小些, 故笔者使用峰面积代替峰高表示吸收强度。另外, 比尔定律只适用于吸光度光谱, 在进行定量分析时, 应先将透射率光谱转化为吸光度光谱。

1.1 基质沥青与SBS改性剂红外光谱分析

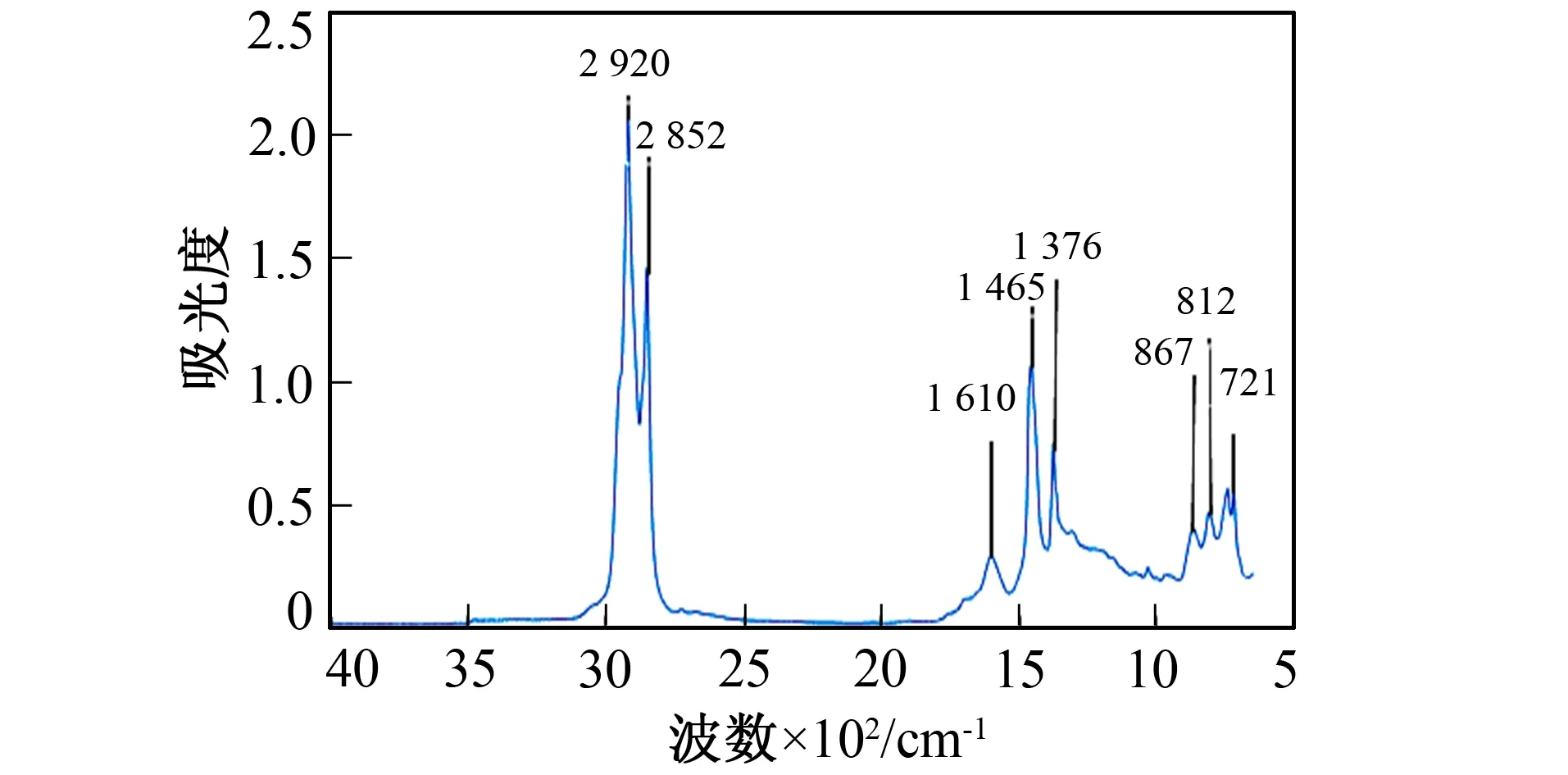
图1 基质沥青的红外光谱图Fig.1 FTIR spectra of matrix asphalt

利用傅里叶变换红外光谱仪采集基质沥青特征红外光谱, 如图1所示。由图1可知, 基质沥青在波数2 800～3 000 cm-1范围的吸收峰是由环烷烃和烷烃的C-H伸缩振动造成的结果； 波数1 376 cm-1和波数1 465 cm-1的吸收峰是由芳香族的甲基和亚甲基的弯曲振动造成的； 波数650～910 cm-1处的吸收峰是由苯环上C-H面外摇摆振动形成的[12]。SBS改性剂是由苯乙烯和丁二烯聚合得到的共聚物, 聚苯乙烯段中苯环和聚丁二烯中的双键是SBS改性剂特征官能团。故其红外光谱主要有两个较强的吸收峰, 波数699 cm-1处的吸收峰是聚苯乙烯造成的； 波数966 cm-1处的吸收峰是聚丁二乙烯造成的。由图2可知, 基质沥青和改性沥青光谱图的差异主要表现在波数为966 cm-1和699 cm-1处, 其他位置十分相似, 只是在某些局部位置的吸收强度出现微小的差异, 可以忽略不计[13]。由图3可知, 基质沥青在波数966 cm-1和699 cm-1处并没有吸收峰, 但红外光谱具有加和性, 所以改性沥青在此两处具有吸收峰, 即由于SBS的存在造成改性沥青在这两处出现吸收峰, 所以这两处特征吸收峰能成为定量测定SBS含量的关键点[14]。笔者选取波数1 376 cm-1作为基质沥青的特征吸收峰, 波数966 cm-1作为SBS改性剂的特征吸收峰来定量测定SBS含量。

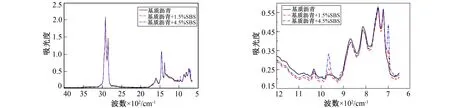
图2 不同SBS含量与基质沥青全局光谱图 图3 不同SBS含量与基质沥青局部光谱图 Fig.2 FTIR spectra of matrix asphalt, Fig.3 Local FTIR spectra of matrix asphalt, modifiedasphalt with different SBS content modified asphalt with different SBS content

1.2 复化辛普生计算吸收峰峰面积

由于得到的红外光谱曲线数据是由若干个离散点组成的, 并不知道光谱曲线的函数关系表达式, 面对这样的情况, 主要用数值积分计算法求积分值, 用拉格朗日插值法构造一个近似被积函数。

在数值积分计算时, 从梯形求积公式和辛普生求积公式的余项中可以看到, 当积分区间长度(b-a)很大时, 数值积分的值将会产生很大的误差, 甚至会以ο(b-a)3,ο(b-a)5的速度产生计算误差。但是, 复化辛普生方法是将区间的长度尽量的缩小, 从而降低计算误差[15], 如图4所示。

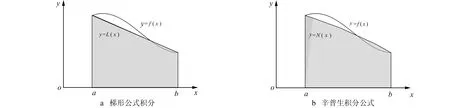
图4 梯形公式积分与辛普生积分公式Fig.4 Trapezoid integral and Spson integral equation

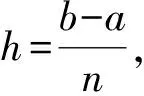
(2)

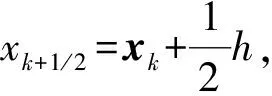
(3)

在计算吸收峰峰面积, 通常有两个值: 经过基线校正过后的峰面积和未经基线校正的峰面积, 基线校正的基线可以人为确定。一般认为定量分析时, 采用校正后的峰面积精度更高, 故笔者选用校正后的峰面积, 其中校正基线选择特征峰两侧最低点的连线, 如图5所示。

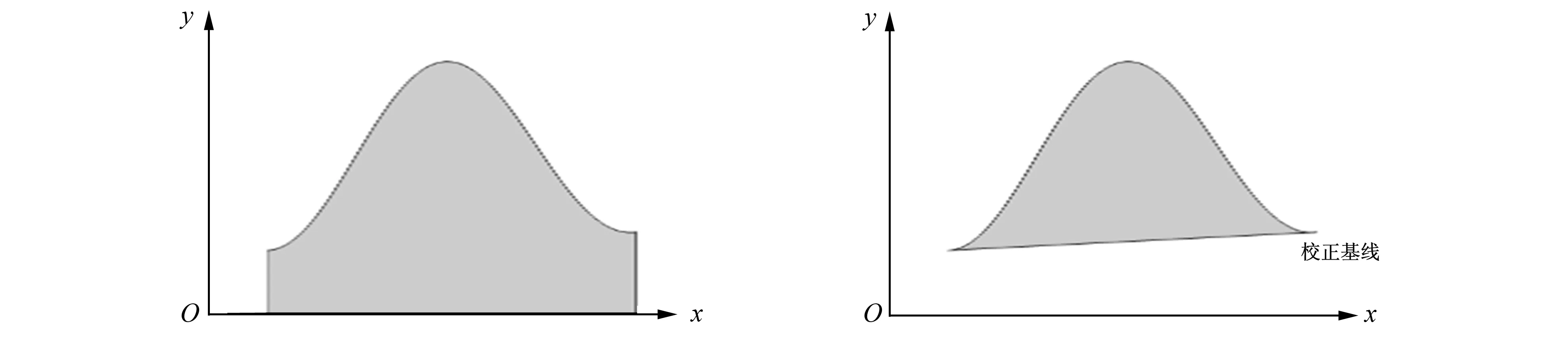
a 校正前峰面积 b 校正后的峰面积图5 校正前峰面积与校正后峰面积Fig.5 Trapezoid integral and Simpson integral equation

2 SBS含量测定方法

2.1 SBS定量分析模型的建立

根据上述朗伯-比耳定律, 物质的浓度跟吸收峰峰面积具有线性相关, 令[x1,x2,…,xn]代表不同改性沥青样本的SBS含量, [y1,y2,…,yn]代表其相对应特征吸收峰峰面积比(A966/A1 376), 则特征吸收峰峰面积Y与SBS含量X具有Y=AX+b关系。若将所有的点(xn,yn)代入式(3)中得到的所有的有关a和b等式联立起来是不存在解。任何a、b都会带来误差, 于是转变为想找到a、b的值使误差和最小, 及是最小二乘法原理。

线性最小二乘法一般表达式, 所有样本自变量组成的矩阵为

(4)

样本应变量组成的矩阵为

(5)

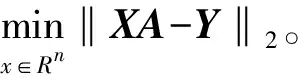
(6)

对目标函数化简

(7)

求导得到

(8)

求得

A=(XTX)-1XTY(9)

最终得到拟合后的标准曲线为Y=XA。

2.2 模型应用

采用辽河石化70#基质沥青按照严格工艺制备含量为1.5%、3%、4.5%、7.5%的SBS改性沥青样本各6组, 获取扫描次数64次、 分辨率4 cm-1、 被检索区域为3 999.64～649.89 cm-1的红外光谱图, 其中3组作为标定模型数据集, 3组作为校正集。按照复化辛普生积分公式求得波数966 cm-1与1 376 cm-1峰面积, 然后计算峰面积比值A966/A1 376, 结果如表1所示。

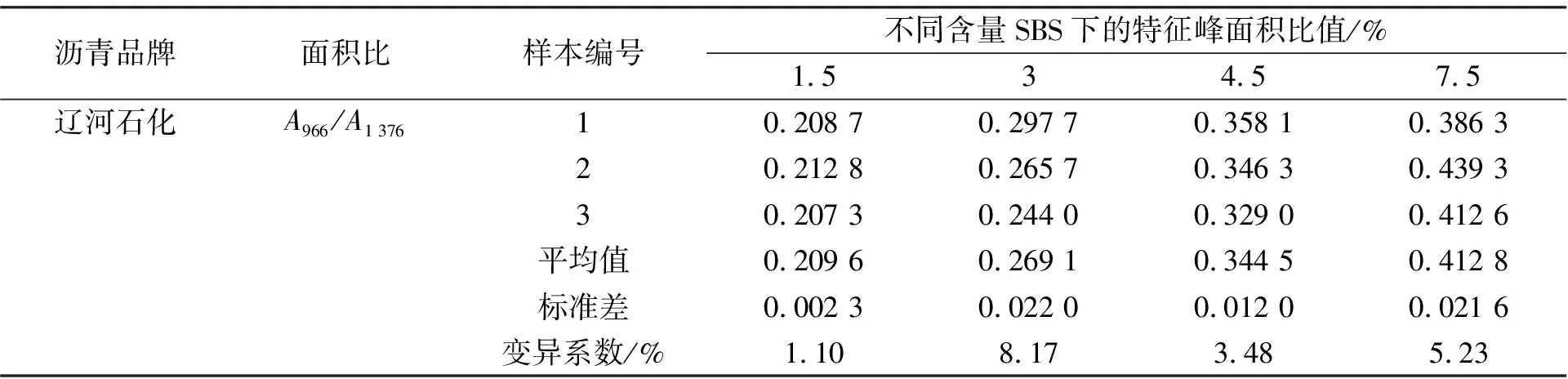
表1 不同SBS含量特征峰面积比值

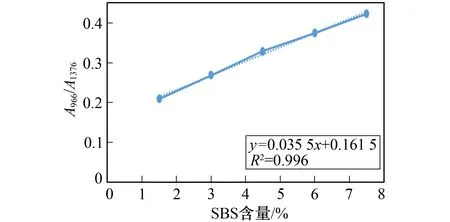
图6 SBS含量测定标准曲线Fig.6 Standard curve of SBS content determination

由表1可知, 不同SBS含量沥青面积比的标准差都非常小, 变异系数均在合理的范围内, 这表明数据稳定性高、 实验误差低, 即用波数966 cm-1与1 376 cm-1的面积比标定模型是符合要求的。

图6为SBS含量测定标准曲线。由图6可见, SBS改性剂含量与特征吸收峰峰面积比存在显著的线性关系, 故设特征峰吸收峰峰面积比Y与SBS含量X存在Y=AX+b的关系式, 按照式(9)求得标准曲线的方程为y=0.035 4x+0.161 5, 相关系数R=0.995 5。

2.3 结果分析

为检验模型的可靠性, 在相同的工艺条件下, 用辽河石化基质沥青制备SBS含量为6%的测试样本3组, 利用上述得到的标准曲线依次计算各样本的SBS含量的测定值, 最后得到数据如表2所示。

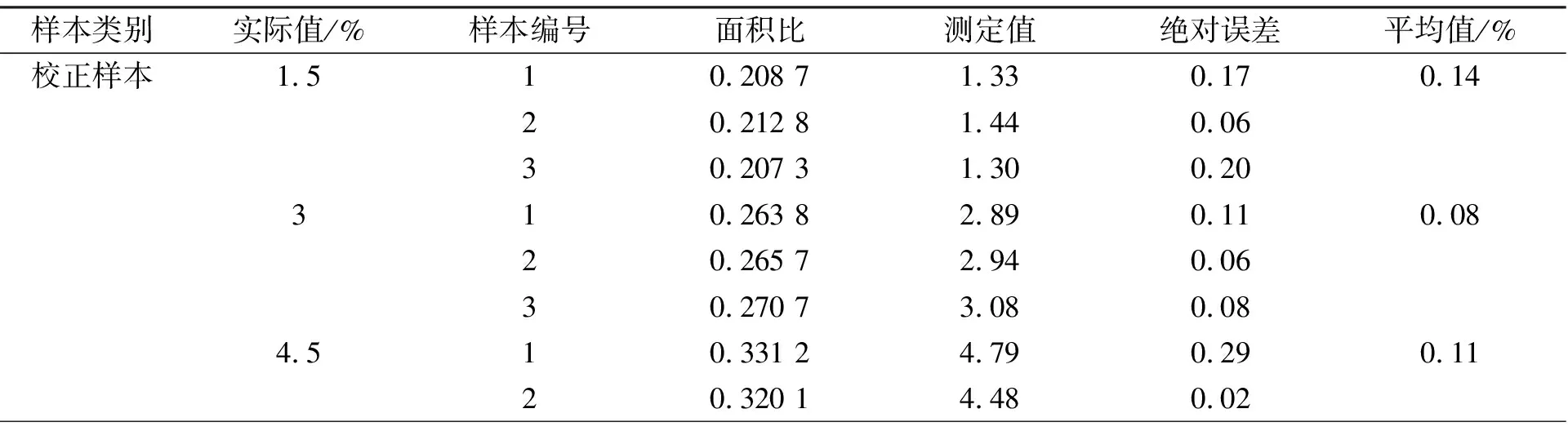
表2 不同含量SBS测定值

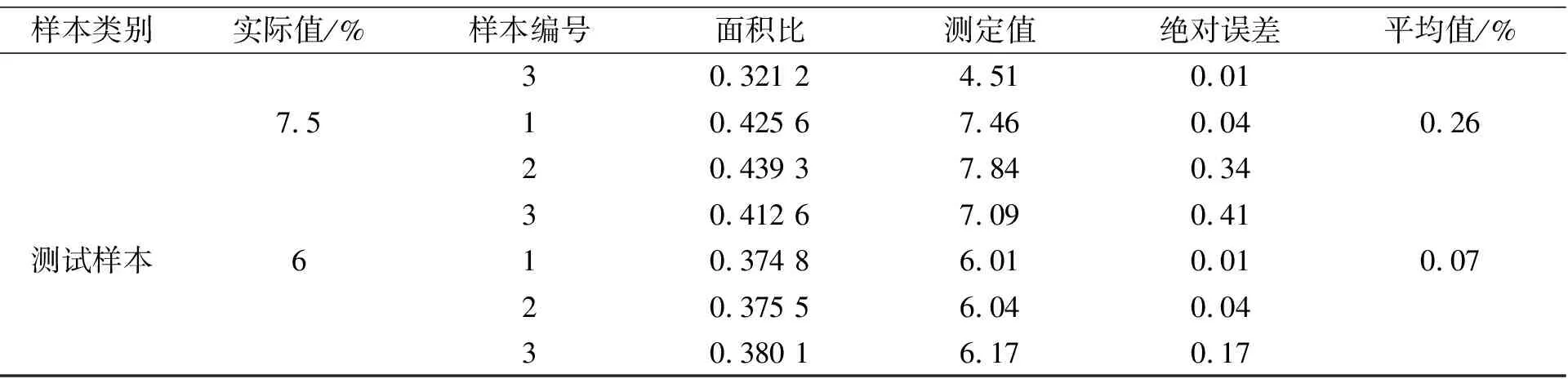
(续表2)

由表2可知, 测试样本绝对误差的平均值为0.07%, 而各校正样本的绝对误差平均值在0.2%左右, 这说明该模型是可靠的, 及工程上利用红外光谱测定沥青SBS含量是可行。

3 结 语

运用红外光谱分析技术结合朗伯-比耳定律对沥青SBS含量测定进行建模, 摆脱对特定红外光谱软件的依赖, 实现了数据获取、 处理、 模型建立与SBS测定一体化。首先对基质沥青和不同SBS含量沥青光谱分析, 确定了波数1 376 cm-1和966 cm-1分别是基质沥青和SBS改性剂的特征“指纹”。然后引入复化辛普生求积公式计算基线校正后的峰面积, 利用最小二乘法拟合出一条标准曲线, 通过曲线相关系数R2发现沥青的SBS改性剂含量与特征峰峰面积比存在显著的线性关系。最后对该曲线进行校正和验证, 结果表明该模型的准确度高, 故利用红外光谱技术测定SBS改性剂含量在工程上是可行的。