机施有机肥散体颗粒离散元模型参数标定

袁全春，徐丽明，邢洁洁，段壮壮，马 帅，于畅畅，陈 晨



机施有机肥散体颗粒离散元模型参数标定

袁全春，徐丽明※，邢洁洁，段壮壮，马 帅，于畅畅，陈 晨

（中国农业大学工学院，北京 100083）

针对有机肥离散元模型接触参数和接触模型参数难以通过查阅文献或试验直接获得的问题，该文提出一种通过仿真试验建立回归模型并结合物理试验寻优的方法，对有机肥离散元模型参数进行标定。考虑到有机肥颗粒间的凝聚力，选择“Hertz-Mindlin with Johnson-Kendall-Roberts”接触模型。应用Plackett-Burman Design对有机肥离散元模型参数进行筛选，得到对休止角有显著影响的参数，即有机肥-有机肥滚动摩擦系数、表面能JKR和有机肥-钢板滚动摩擦系数；通过最陡爬坡试验确定了显著性参数的最优值区间，应用Central Composite Design建立并优化了休止角与显著性参数的回归模型，以实际休止角为目标，求解得到显著性参数最优值，即有机肥-有机肥滚动摩擦系数为0.10，JKR为0.015，有机肥-钢板滚动摩擦系数为0.11。在标定的参数下进行仿真验证试验，仿真休止角与实际休止角的相对误差为0.42%，无明显差异，表明标定的参数准确，可以为有机肥离散元模型参数的选取提供参考。

模型；肥料；离散元；参数标定；凝聚力；休止角

0 引 言

随着现代化种植管理技术的提高，人们对果园施肥机械的要求也越来越高。基于离散元法[1-2]建立的农业散体颗粒模型具有较高的准确性，应用离散元法研究有机肥与施肥机械的作用机理，可以提高研发效率，改善机械作业性能，为农机具的设计及优化提供理论依据[3-5]。应用离散元法需要在EDEM软件中建立有机肥模型，并定义模型的参数，模型参数的准确性将直接影响研究结果的可靠性。模型参数包括材料本征参数（粒径、泊松比、剪切模量和密度）、接触参数（碰撞恢复系数、静摩擦系数和滚动摩擦系数）和接触模型参数（Bonding模型的法/切向模量、Johnson-Kendall-Roberts模型的表面能JKR等）。材料本征参数正常是固定的，通常可以通过查阅文献和试验测定得到；而接触参数和接触模型参数很难直接获得，通常需要通过仿真试验进行标定[6]。目前，在农业工程领域，很多学者在农业散体颗粒的离散元模型参数标定方面做了大量的工作，但对于有机肥离散元模型参数标定的研究较少。

王云霞等[7]基于休止角试验仿真标定了玉米种子间静摩擦系数和滚动摩擦系数；刘凡一等[8]标定了小麦的离散元模型参数；石林榕等[9]标定了西北旱区农田土壤离散元模型参数；王宪良等[10]标定了土壤颗粒间静摩擦系数和滚动摩擦系数；张锐等[11]通过仿真标定，得出颗粒外观形貌对颗粒间静摩擦系数影响较大的结论；武涛等[12]基于休止角试验标定了粘性土壤的离散元模型参数。

本文拟针对样品有机肥，应用EDEM软件，选择“Hertz-Mindlin with Johnson-Kendall-Roberts”凝聚力接触模型，进行Plackett-Burman Design、最陡爬坡试验和Central Composite Design等有机肥休止角仿真试验，并结合有机肥休止角物理试验对有机肥离散元模型参数进行标定。以期获得较为准确的有机肥离散元模型参数，为有机肥离散元模型参数的选取提供参考。同时，提供一种通过测定易于测定的参数（休止角）来推导难以测定的有机肥离散元模型参数的方法。

1 材料与方法

1.1 有机肥基本参数

本文所用有机肥为兰州花海镇紫龙珠葡萄合作社的有机肥，由纯羊粪发酵得到。为满足施肥均匀性的要求，对结块有机肥进行粉碎处理。有机肥的基本参数如表1所示。

1.2 试验方法

本文采用物理试验与仿真试验相结合的方法[13-14]对有机肥离散元模型参数进行标定。首先进行物理试验，采用圆筒提升的方法获得有机肥颗粒堆，并测量有机肥实际休止角。然后利用软件EDEM2.6进行仿真试验，先通过Plackett-Burman Design对有机肥离散元模型参数进行筛选，得到对休止角有显著影响的参数；再通过最陡爬坡试验确定显著性参数的最优值区间，通过Central Composite Design响应面分析方法建立并优化有机肥休止角与显著性参数的回归模型，得到回归方程，以实际休止角为目标值对回归方程求解寻优，得到显著性参数最优值。最后在标定的参数下进行仿真试验，对比有机肥仿真休止角和实际休止角，验证标定的有机肥离散元模型参数的准确性。不同的物料对休止角有显著影响的离散元模型参数是有差异的，先进行筛选可以针对有机肥的特性进行标定。与正交试验相比，采用响应面分析方法建立的回归模型是连续的，寻优得到的最优值更准确。

表1 有机肥基本性质

1.3 有机肥休止角物理试验

本文采用圆筒提升的方法进行试验[15]，如图1所示。试验时，首先使钢质圆筒（内径40 mm、高80 mm）底面与钢板（长400 mm、宽200 mm）接触，然后向钢质圆筒内填充有机肥直至填满。使用REGER万能试验机将钢质圆筒以20 mm/s的速度向上提升，从而使有机肥形成一个颗粒堆，最后使用三量181-101型数显倾角仪（分辨率：0.05°，精度：±0.2°）测量有机肥休止角。该试验重复10次，取平均值，最终得到有机肥实际休止角为38.15°。

图1 有机肥休止角物理试验

1.4 仿真模型

1.4.1 接触模型

有机肥颗粒间受水分和化学物质的作用存在粘附现象，普通的接触模型难以准确地模拟施肥机械作业过程中有机肥的力学行为。本文选择“Hertz-Mindlin with Johnson-Kendall-Roberts”接触模型[16]，该模型是一个凝聚力接触模型，可以考虑在接触区域中范德华力的影响和允许用户模拟强黏性的系统，如干燥的粉末或湿颗粒。在这个模型中，切向弹性力、法向耗散力和切向耗散力均与Hertz-Mindlin(no slip)接触模型中的计算方法一致，但JKR法向弹性力的实现基于Johson-Kendall-Roberts理论，取决于重叠量、相互作用参数和表面能

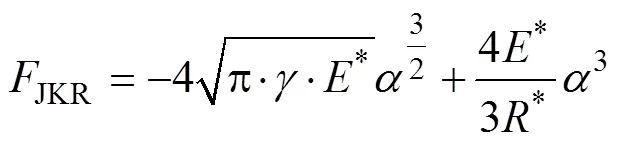
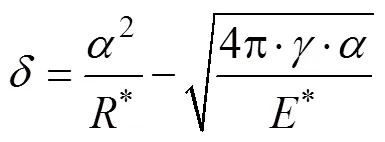
式中JKR为JKR法向弹性力，N；为相互接触的两个颗粒的接触圆半径，m；为重叠量，m为表面能，N/m；E为当量弹性模量，Pa；R为当量半径，m。当量弹性模量和当量半径定义为

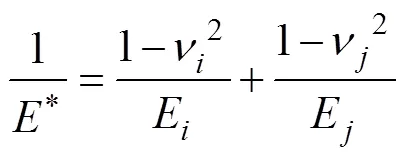
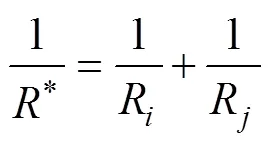
式中E，ν，R和E，ν，R分别为相互接触的2个颗粒的弹性模量、泊松比和半径。

当=0时，力变成Hertz-Mindlin法向力

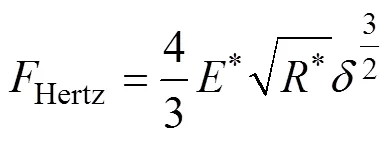
即使颗粒并不是直接接触，该模型也提供吸引凝聚力，颗粒间具有非零凝聚力的最大间隙为

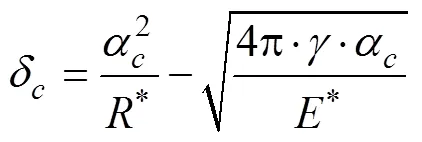
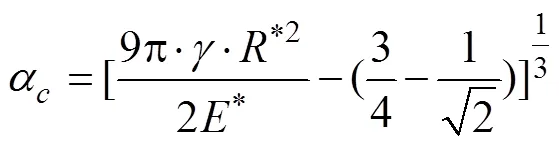
式中δ为颗粒间具有非零凝聚力时的法向最大间隙，m；α为2个颗粒的接触圆半径，m。

当颗粒并非实际接触并且间隙小于δ时，凝聚力达到最大值

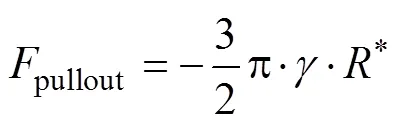
摩擦力的计算和Hertz-Mindlin(no slip)接触模型不同，不同在于它是取决于JKR法向力的正向排斥部分。因此，该模型在接触力的凝聚力分量更大时提供一个更大的摩擦力。

1.4.2 有机肥和结构模型

在进行仿真前必须要先建立有机肥和结构的模型，有机肥颗粒近似球形，故以基本球体作为有机肥模型。仿真试验表明：相同条件下，仅建立半径1 mm的有机肥模型形成的休止角与根据粒径分布建立多种半径的有机肥模型形成的休止角的相对误差为2.22%。考虑到颗粒半径太小会影响计算速度，本文仅建立半径1 mm（占比最大）的有机肥模型。在SolidWorks中建立钢质圆筒和钢板的三维模型，并导入EDEM2.6中作为结构模型。通过试验和查阅相关文献[17-22]，得到有机肥和钢板的本征参数，如表2所示。

1.4.3 仿真参数的设置

本文在进行仿真试验[23]时，设置钢质圆筒的提升速度20 mm/s（此速度下可以较好地形成肥堆），生成颗粒总数量10 000个，生成速率2 000个/s，固定时间步长是Rayleigh时间步长的22%，数据保存时间间隔为0.01 s，网格大小为2 mm。

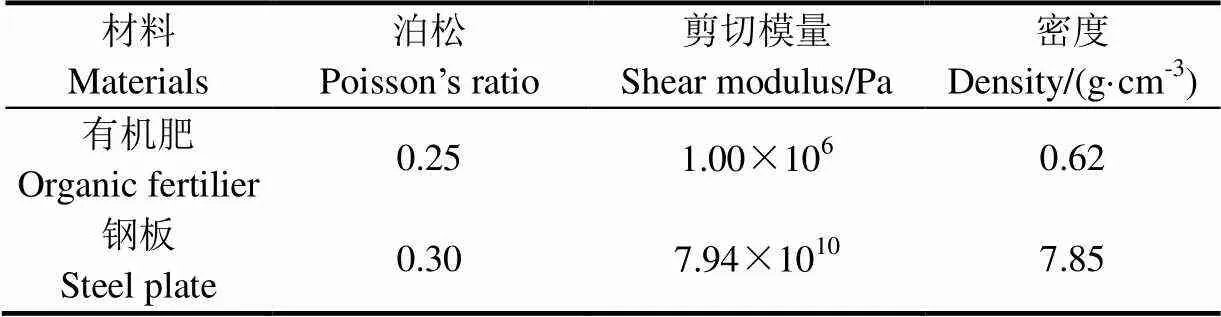
表2 有机肥、钢板本征参数

1.5 仿真试验

1.5.1 Plackett-Burman Design筛选显著性参数

接触参数和接触模型参数中并不是所有参数都对休止角有显著影响[24-26]，没有显著影响的参数并不能基于休止角来标定，否则标定出的参数是不准确的。所以本文应用软件Design Expert 8.0.6[27-28]进行Plackett-Burman Design[29]，对接触参数（有机肥-有机肥恢复系数、有机肥-有机肥静摩擦系数、有机肥-有机肥滚动摩擦系数、有机肥-钢板恢复系数、有机肥-钢板静摩擦系数和有机肥-钢板滚动摩擦系数）和接触模型参数（JKR）进行筛选，筛选出对有机肥休止角有显著影响的参数。

参考文献[17-21]中，有机肥颗粒间的恢复系数范围为0.1~0.6，静摩擦系数范围为0.3~1，滚动摩擦系数范围为0.1~0.5；有机肥颗粒与钢板间的恢复系数范围为0.048~0.6，静摩擦系数范围为0.2~0.86，滚动摩擦系数范围为0.1~0.5。通过综合对比参考文献中肥料和本文中有机肥特性的差异，确定了接触参数的取值范围，并通过仿真预试验确定了JKR的取值范围。Plackett-Burman Design的因素水平如表3所示，共7个因素，各取1个高水平、1个低水平，并选择1个中心点；试验方案及结果如表4所示，设置4个空白列用于误差分析，共进行13次试验。

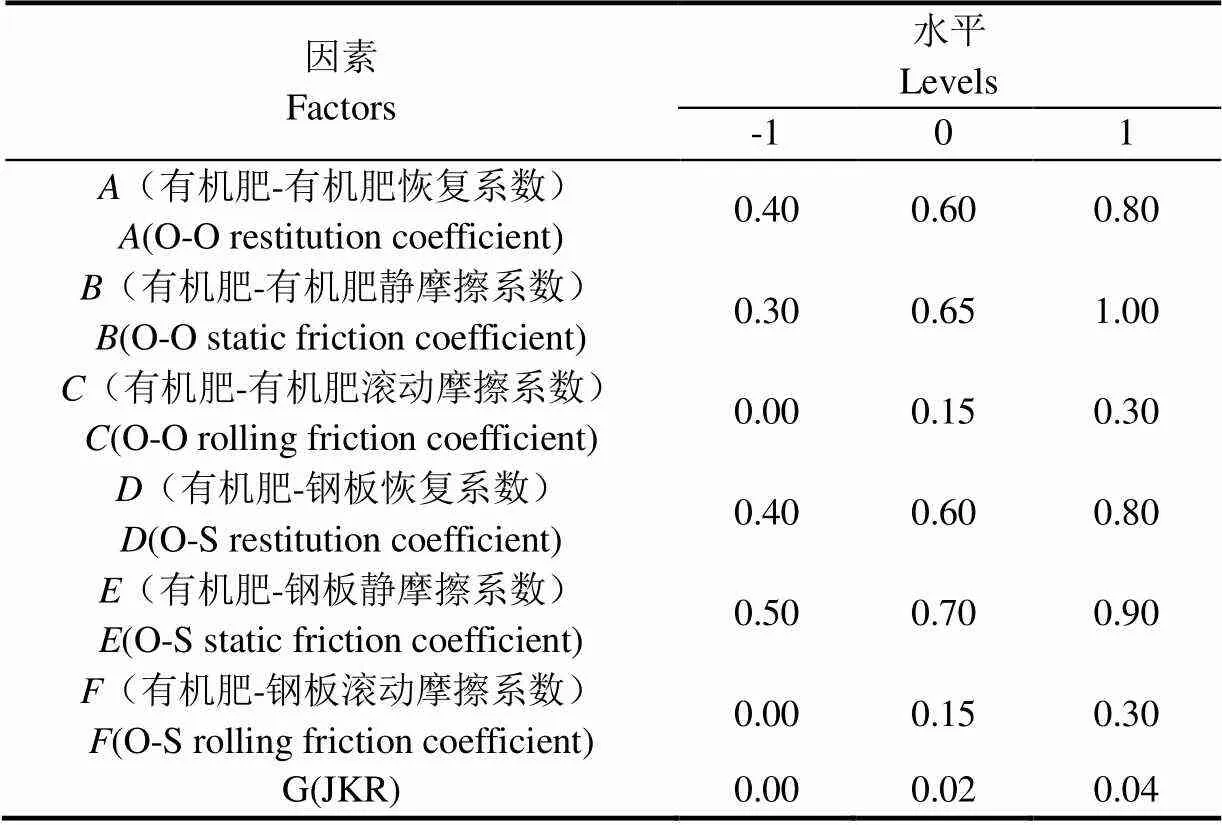
表3 Plackett-Burman Design因素水平表

注：O为有机肥；S为钢板；JKR为表面能

Note: O is organic fertilizer, S is steel plate and JKR is surface energy.

利用软件Design Expert 8.0.6对试验结果进行方差分析，得到7个参数对休止角的影响效果和显著性，如表5所示。由表5可知，7个参数对休止角的效应均是正效应，即休止角随着参数的增大而增大；其中对休止角影响显著（<0.05）的参数包括：有机肥-有机肥滚动摩擦系数（）、JKR（）和有机肥-钢板滚动摩擦系数（），而其余参数影响不显著。分析得出，恢复系数对休止角影响不显著的原因在于基于休止角的试验中不存在明显的弹性碰撞，而静摩擦系数没有显著影响的原因在于有机肥颗粒的形状，有机肥颗粒是球形颗粒，相比于玉米等非球形颗粒，滚动摩擦系数对休止角的影响要比静摩擦系数显著。

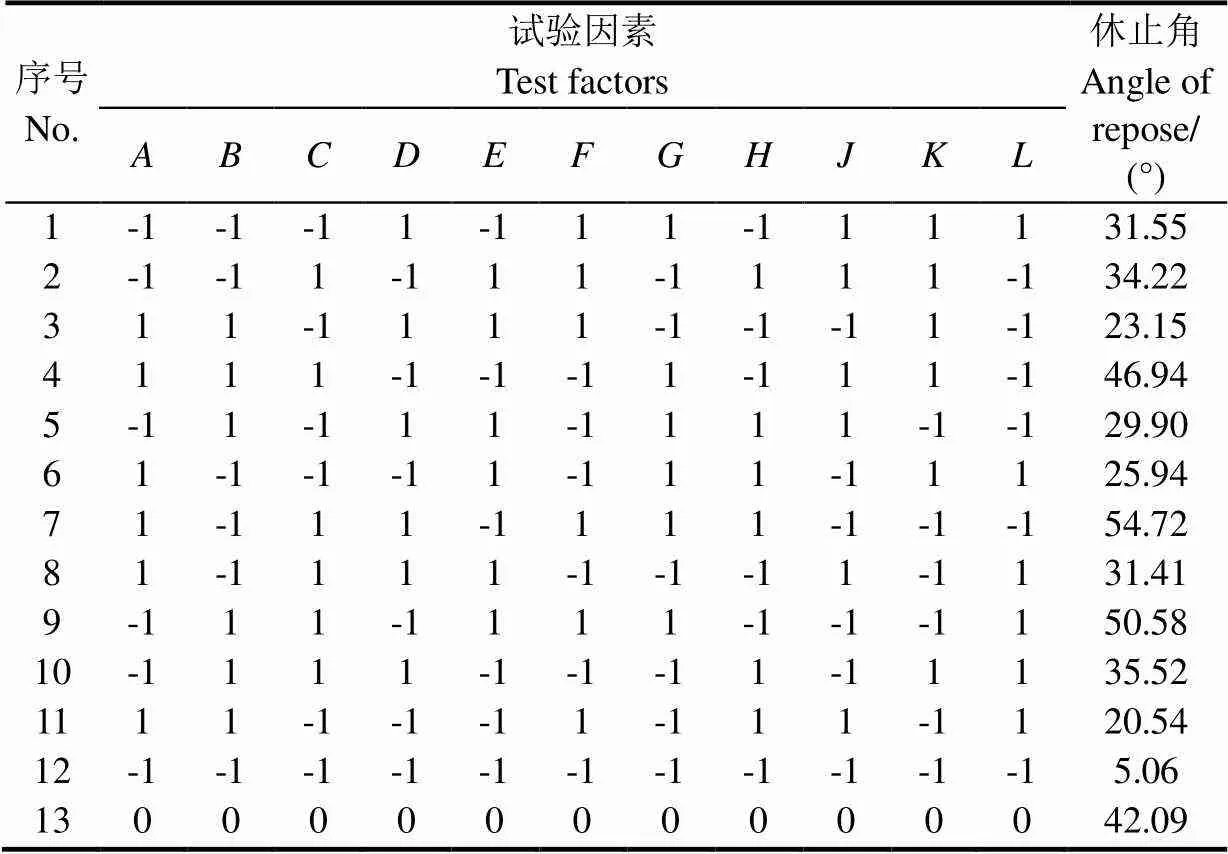
表4 Plackett-Burman Design方案及结果

注：，，，为空白列。

Note:,,andindicates blank column.

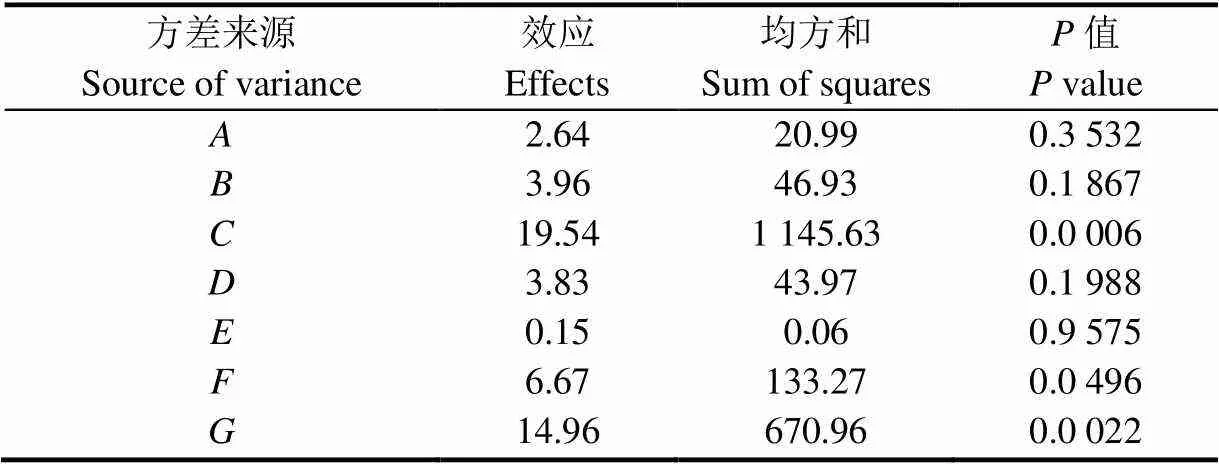
表5 Plackett-Burman Design试验结果方差分析

1.5.2 最陡爬坡试验确定显著性参数最优值区间

应用响应面分析方法建立回归模型求解最优值的前提是因素的最优值在所选高低水平范围内，最陡爬坡试验可以较快地确定因素最优值所在区间。根据Plackett-Burman Design的试验结果，本文只将3个显著性参数（有机肥-有机肥滚动摩擦系数、JKR和有机肥-钢板滚动摩擦系数）按照选定步长逐步增加（参数影响效应是正效应)，其余参数选择中间水平（有机肥-有机肥恢复系数0.6、有机肥-有机肥静摩擦系数0.65、有机肥-钢板恢复摩擦系数0.6、有机肥-钢板静摩擦系数0.7）进行最陡爬坡试验，并计算有机肥仿真休止角与实际休止角的相对误差，试验方案及结果如表6所示。

由表6可知，随着有机肥-有机肥滚动摩擦系数（）、JKR（）和有机肥-钢板滚动摩擦系数（）的增大，有机肥仿真休止角不断增大，仿真休止角与实际休止角的相对误差先减小后增大。第2组试验的相对误差最小，所以3个显著性参数的最优区间在第2组试验所选的水平附近，因此选择第1、2、3组试验所选的水平进行响应面分析试验，建立回归模型求解显著性参数的最优值。

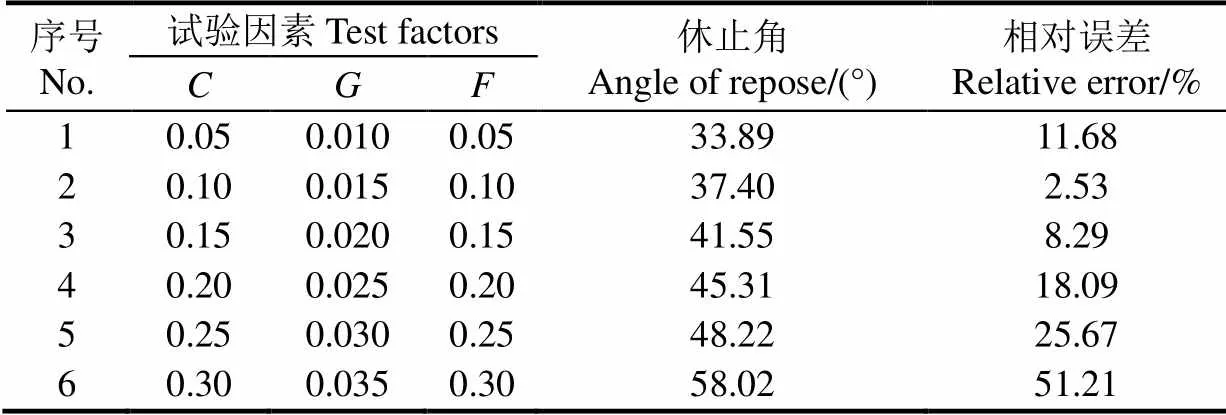
表6 最陡爬坡试验方案及结果

1.5.3 响应面分析试验建立回归模型求解显著性参数最优值

根据最陡爬坡试验结果，进行Central Composite Design响应面[30]分析试验。试验中，非显著性参数同样选择中间水平（有机肥-有机肥恢复系数0.6、有机肥-有机肥静摩擦系数0.65、有机肥-钢板恢复摩擦系数0.6、有机肥-钢板静摩擦系数0.7），显著性参数水平如表7所示，各取5个水平。选择6个中心点进行误差估计，试验方案及结果如表8所示，共进行20次试验，包括6次中心点的重复试验。

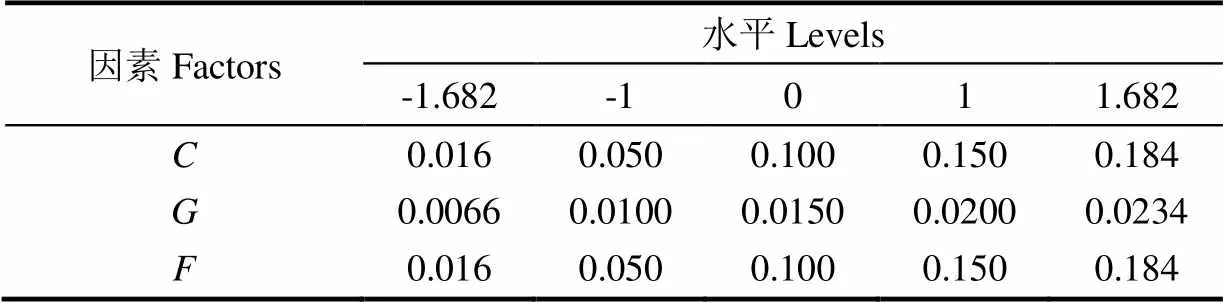
表7 Central Composite Design因素水平表

表8 Central Composite Design方案及结果

应用软件Design Expert 8.0.6对试验结果进行分析，得到二次回归模型。该二次回归模型的方差分析如表9所示，有机肥-有机肥滚动摩擦系数（）和JKR（）对有机肥休止角的影响十分显著（<0.01）；该线性回归模型<0.01，说明休止角与所得回归方程关系是极显著的；失拟项=0.051 9>0.05，说明所得回归方程与实际拟合中非正常误差所占比例小，拟合性较好。本试验的变异系数CV=2.06%，故本试验可靠性较好；决定系数2=0.965 5和校正决定系数2adj=0.934 5，接近1，故所得回归方程可靠度较高；精确度Adeq Precision=20.458，故该回归模型精确度良好。

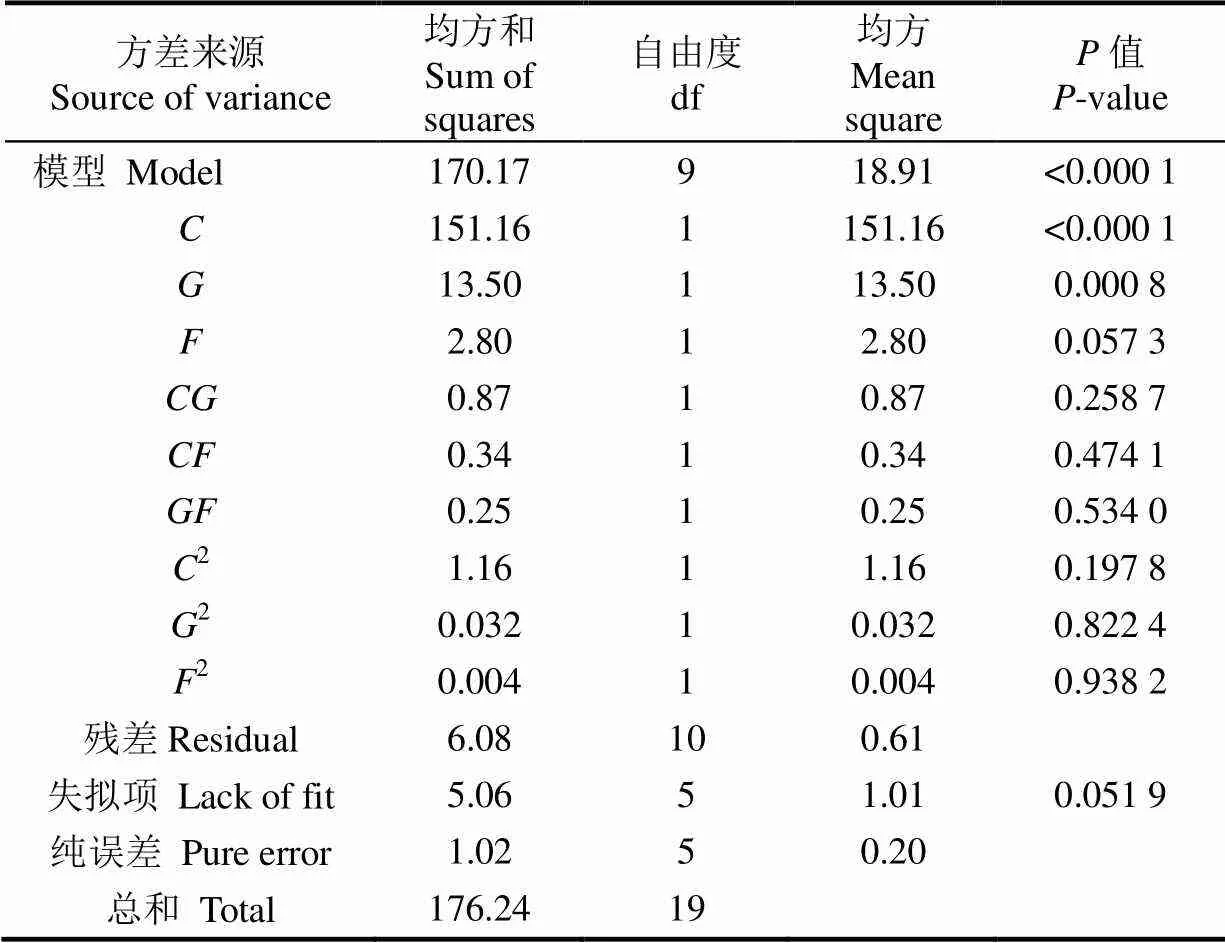
表9 Central Composite Design二次回归模型方差分析

通过剔除影响非常不显著的项，并尝试添加三次项对二次回归模型进行优化。优化后的回归模型方差分析如表10所示，失拟项=0.405 6、变异系数CV=1.30%、决定系数2=0.980 7、校正决定系数2adj=0.973 8、精确度Adeq Precision=45.591。较优化前，所得回归方程在拟合性、可靠性和精确性等方面都有很大改善。优化后的回归方程为

=23.605 72+215.056 53+198.853 17

+9.059-1586.300 932+4906.266 463（9）

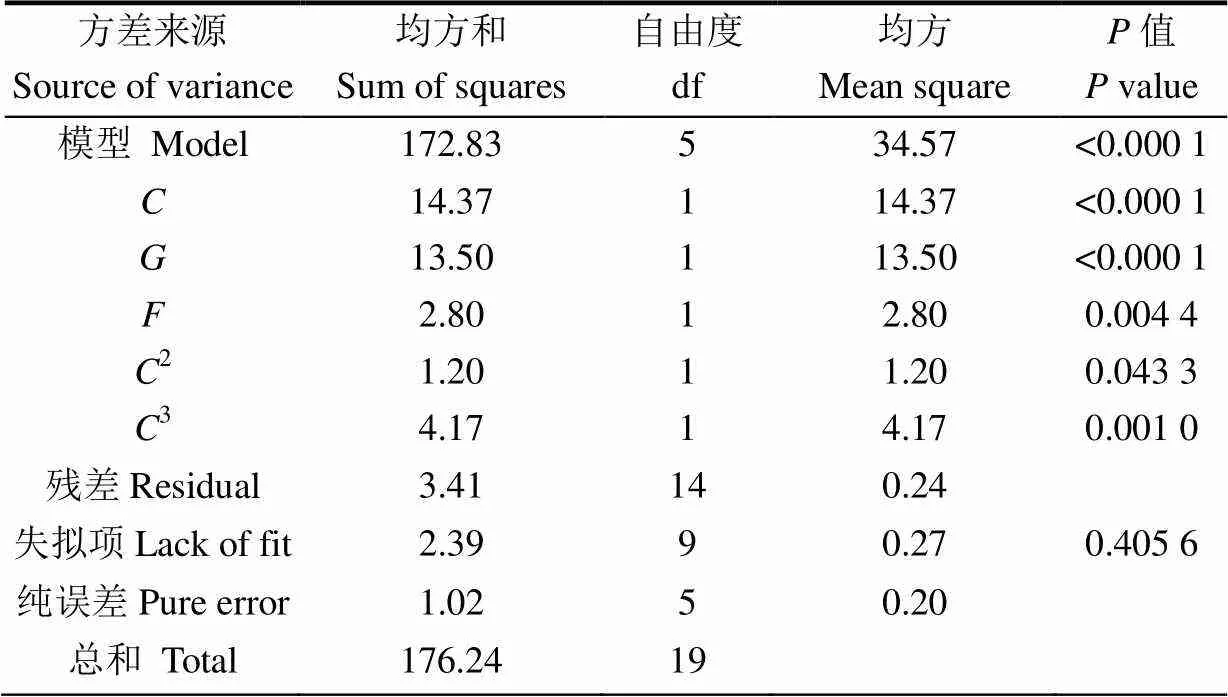
表10 Central Composite Design优化回归模型方差分析

应用软件Design Expert 8.0.6以有机肥实际休止角为目标对优化后的回归方程求解寻优，得到3个显著性参数的最优值，有机肥-有机肥滚动摩擦系数为0.10，JKR为0.015，有机肥-钢板滚动摩擦系数为0.11。

2 验证试验

为了验证所得3个显著性参数最优值的准确性，本文将3个显著性参数设置为最优值（有机肥-有机肥滚动摩擦系数0.10、JKR 0.015、有机肥-钢板滚动摩擦系数0.11），非显著性参数同样选择中间水平（有机肥-有机肥恢复系数0.6、有机肥-有机肥静摩擦系数0.65、有机肥-钢板恢复摩擦系数0.6、有机肥-钢板静摩擦系数0.7），其他设置不变，应用软件EDEM 2.6进行有机肥休止角仿真试验，测得有机肥仿真休止角为37.99°。与有机肥实际休止角38.15°的相对误差为0.42%，无显著性差异，说明所得3个显著性参数的最优值准确可靠。仿真试验与物理试验的对比如图2所示，两者有机肥颗粒堆轮廓十分接近。

图2 仿真试验与物理试验对比

3 结 论

1）通过Plackett-Burman Design筛选出对有机肥休止角有显著影响的接触参数和模型参数包括：有机肥-有机肥滚动摩擦系数、表面能JKR和有机肥-钢板滚动摩擦系数。

2）通过最陡爬坡试验确定了3个显著性参数的最优值区间，通过Central Composite Design响应面分析试验建立并优化了有机肥休止角与显著性参数之间的回归模型，对优化后的回归模型方差分析发现，除了3个显著性参数对有机肥休止角影响显著外，有机肥-有机肥滚动摩擦系数的二次项和三次项对有机肥休止角也有显著影响。

3）以有机肥实际休止角为目标值，对优化后的回归方程进行寻优求解，得到3显著性参数的最优值，有机肥-有机肥滚动摩擦系数为0.10，表面能JKR为0.015，有机肥-钢板滚动摩擦系数为0.11。对比验证试验结果表明，有机肥仿真休止角与实际休止角无显著差异，所标定的有机肥离散元模型参数准确可靠。

[1] Cundall P A, Strack O D L. A discrete numerical method for granular assemblis[J]. Geptechnique, 1979, 29(1): 47－65.

[2] 胡国明. 颗粒系统的离散元素法分析仿真—离散元素法的工业应用与EDEM软件简介[M]. 武汉：武汉理工大学出版社，2010.

[3] 贺一鸣，吴明亮，向伟，等. 离散元法在农业工程领域的应用进展[J]. 中国农学通报，2017，33(20)：133－137. He Yiming, Wu Mingliang, Xiang Wei, et al. Application progress of discrete element method in agricultural engineering[J]. Chinese Agricultural Science Bulletin, 2017, 33(20): 133－137. (in Chinese with English abstract)

[4] 于建群，付宏，李红，等. 离散元法及其在农业机械工作部件研究与设计中的应用[J]. 农业工程学报，2005，21(5)：1－6. Yu Jianqun, Fu Hong, Li Hong, et al. Application of discrete element method to research and design of working parts of agricultural machines[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(5): 1－6. (in Chinese with English abstract)

[5] 马征，李耀明，徐立章. 农业工程领域颗粒运动研究综述[J]. 农业机械学报，2013，44(2)：22－29. Ma Zheng, Li Yaoming, Xu Lizhang. Summarize of particle movements research in agricultural engineering realm[J]. Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(2): 22－29. (in Chinese with English abstract)

[6] 龚明. 材料物料特性参数标定[R]. 北京：EDEM用户大会报告，2013.

[7] 王云霞，梁志杰，张东兴，等. 基于离散元的玉米种子颗粒模型种间接触参数标定[J]. 农业工程学报，2016，32(22)：36－42. Wang Yunxia, Liang Zhijie, Zhang Dongxing, et al. Calibration method of contact characteristic parameters for corn seeds based on EDEM[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(22): 36－42. (in Chinese with English abstract)

[8] 刘凡一，张舰，李博，等. 基于堆积试验的小麦离散元参数分析及标定[J]. 农业工程学报，2016，32(12)：247－253. Liu Fanyi, Zhang Jian, Li Bo, et al. Calibration of parameters of wheat required in discrete element method simulation based on repose angle of particle heap[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(12): 247－253. (in Chinese with English abstract)

[9] 石林榕，赵武云，孙伟. 基于离散元的西北旱区农田土壤颗粒接触模型和参数标定[J]. 农业工程学报，2017，33(21)：181－187. Shi Linrong, Zhao Wuyun, Sun Wei. Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 181－187. (in Chinese with English abstract)

[10] 王宪良，胡红，王庆杰，等. 基于离散元的土壤模型参数标定方法[J]. 农业机械学报，2017，48（12）：78－85. Wang Xianliang, Hu Hong, Wang Qingjie, et al. Calibration method of soil contact characteristic parameters based on DEM theory[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(12): 78－85. (in Chinese with English abstract)

[11] 张锐，韩佃雷，吉巧丽，等. 离散元模拟中沙土参数标定方法研究[J]. 农业机械学报，2017，48（3）：49－56. Zhang Rui, Han Dianlei, Ji Qiaoli, et al. Calibration methods of sandy soil parameters in simulation of discrete element method[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(3): 49－56. (in Chinese with English abstract)

[12] 武涛，黄伟凤，陈学深，等. 考虑颗粒间粘结力的黏性土壤离散元模型参数标定[J]. 华南农业大学学报，2017，38（3）：93－98. Wu Tao, Huang Weifeng, Chen Xueshen, et al. Calibration of discrete element model parameters for cohesive soil considering the cohesion between particles[J]. Journal of South China Agricultural University, 2017, 38(3): 93－98. (in Chinese with English abstract)

[13] Michael R, Kevin J H. A methodical calibration procedure for discrete element models[J]. Powder Technology, 2017, 307: 73－83.

[14] Coetzee C J. Calibration of the discrete element method[J]. Powder Technology, 2017, 310: 104－142.

[15] 田晓红，李光涛，张淑丽. 谷物自然休止角测量方法的探究[J]. 粮食加工，2010，35（1）：68－71. Tian Xiaohong, Li Guangtao, Zhang Shuli. Determination of angle of repose[J]. Grain Processing, 2010, 35(1): 68－71. (in Chinese with English abstract)

[16] DEM Solutions. EDEM 2.6 theory reference guide[M]. Edinburgh: DEM Solutions, 2014.

[17] 张晓明. 有机肥颗粒热风干燥工艺及装备研究[D]. 北京：中国农业大学，2017. Zhang Xiaoming. Study on the Drying Process and Equipment for Organic Fertilizer Rellets[D].Beijing: China Agricultural University, 2017.

[18] 罗帅，袁巧霞，GOUDA Shaban，等. 基于JKR粘结模型的蚯蚓粪机质离散元法参数标定[J]. 农业机械学报，2018，49（4）：343－350.Luo Shuai, Yuan Qiaoxia, GOUDA Shaban, et al. Parameters calibration of vermicomposting nursery substrate with discrete element method based on JKR contact model[J]. ransactions of the Chinese Society of Agricultural Machinery, 2018, 49(4): 343－350. (in Chinese with English abstract)

[19] Landry H, Laguë C, Roberge M. Discrete element representation of manure products[J]. Computers and electronics in agriculture, 2006, 51: 17－34.

[20] Landry H, Thirion F, Laguë C, et al. Numerical modeling of the flow of organic fertilizers in land application equipment[J]. Computers and electronics in agriculture, 2006, 51: 35－53.

[21] Landry H, Laguë C, Roberge M. Physical and rheological properties of manure products[J]. Applied Engineering in Agriculture, 2004, 20(3): 277－288.

[22] 闻邦椿. 机械设计手册(第5版)[M]. 北京：机械工业出版社，2010.

[23] 王国强. 离散单元法及其在EDEM上的实践[M]. 西安：西北工业大学出版社，2010.

[24] 夏鹏，李郁，杨公波. 散粒物料堆积角离散元仿真研究[J]. 起重运输机械，2015（2）；107－110. Xia Peng, Li Yu, Yang Gongbo. Study on the discrete element simulation of scattered materials[J]. Hoisting and Conveying Machinery, 2015(2)：107－110. (in Chinese with English abstract)

[25] 韩燕龙，贾富国，唐玉荣，等. 颗粒滚动摩擦系数对堆积特性的影响[J]. 物理学报，2014，63（17）：4501－4507. Han Yanlong, Jia Fuguo, Tang Yurong, et al. Influence of granular coefficient of rolling friction on accumulation characteristics[J]. Acta Physica Sinica, 2014, 63(17): 4501－4507. (in Chinese with English abstract)

[26] 贾旭光，陈曦，李鑫. 不同粒度和堆载形态下散体瞬时自然安息角的实验研究[J]. 现代矿业，2015，549（1）：25－27. Jia Xuguang, Chen Xi, Li Xin. Experiment research on instantaneous natural repose angle of granular slope under different granularity and stack form[J]. Modern Mining, 2015, 549(1): 25－27. (in Chinese with English abstract)

[27] 徐向宏，何明珠. 试验设计与Design-Expert、SPSS应用[M]. 北京：科学出版社，2010.

[28] 葛宜元. 试验设计方法与Design-Expert软件应用[M]. 哈尔滨：哈尔滨工业大学出版社，2015.

[29] Ledi T, Pat S, Terri M, et al. Plackett-Burman designs[EB/OL]. 2013-10-30[2013-10-30]. http://www.itl. nist.gov/div898/handbook/pri/section3/pri335.html.

[30] Ledi T, Pat S, Terri M, et al. Response surface designs[EB/OL]. 2013-10-30[2013-10-30]. http://www. itl.nist.gov/div898/handbook/pri/section3/pri336.html.

Parameter calibration of discrete element model of organic fertilizer particles for mechanical fertilization

Yuan Quanchun, Xu Liming※, Xing Jiejie, Duan Zhuangzhuang, Ma Shuai, Yu Changchang, Chen Chen

(,,100083,)

As the parameters of discrete element model for organic fertilizer are difficult to obtain directly from literatures or experiments, this study proposed a method to calibrate the parameters based on tests of the angle of repose. Firstly, a physical test was carried out. The diameters of organic fertilizer particles were between 0.25 and 2 mm, the fertilizer moisture was 13.7%, and the organic fertilizer was crushed to meet the requirements of uniformity of fertilization. In the test, in order to obtain the organic fertilizer heap, the cylinder was lifted up by a universal testing instrument at a speed of 20 mm/s. Then, the angle of repose of the fertilizer was measured with inclinometer and the test was repeated for 10 times, as the mean angle of repose was 38.15°. Secondly, the simulation test was carried out. Considering the cohesion characteristics between particles of organic fertilizer, the contact model of Hertz-Mindlin with Johnson-Kendall-Roberts was used in simulation modeling. Since the organic fertilizer particles were near-spherical, the basic model of the software default was adopted to simulate organic fertilizer granules. In the simulation test, the relative error was 2.22% by comparing the angle of repose formed by a variety of particle sizes according to actual particle size distribution and the angle of repose formed by the same particle size (1 mm). Therefore, a basic sphere model with a radius of 1 mm was used and the three-dimension geometry model built by SolidWorks was imported into the simulation software, with the cylinder lifting speed was 20 mm/s, the total number of particles was 10 000, the generation rate was 2 000/s, the fixed time step was 22% of Rayleigh time step, the target save interval was 0.01 s, and the cell size was 2 mm. Not all discrete element model parameters of organic fertilizer had significant impact on the angle of repose, so a screening through Plackett-Burman Design was made. The results showed that rolling friction coefficient between organic fertilizer, surface energy (JKR) and rolling friction coefficient between organic fertilizer and steel plate had significant impact on angle of repose. The optimal value interval of the there significant parameters was determined by the steepest ascent test, and built the linear regression model of angle of repose through Central Composite Design. The fitting of the linear regression model was optimized by adding the quadratic term and cubic term of rolling friction coefficient between organic fertilizer with the fitting of the regression model had a great improvement, and thevalue of the lack of fit was improved from 0.091 to 0.405 6. Thirdly, the optimal value of the significant parameters was obtained with the actual angle of repose as a goal, with the rolling friction coefficient between organic fertilizer was 0.10, the JKR was 0.015, and the rolling friction coefficient between organic fertilizer and steel plate was 0.11. Finally, in order to verify the accuracy of the calibrated parameters, the simulation verification test of the calibration parameters was carried out, and the relative error between the simulated angle of repose and the actual angle of repose is 0.42%, which meant that the calibration parameters were accurate. This study can provide reference for the selection of discrete element model parameters of organic fertilizer.

models; fertilizers; discrete element method; calibration of parameters; cohesion; angle of repose

10.11975/j.issn.1002-6819.2018.18.003

S220.1

A

1002-6819(2018)-18-0021-07

2018-02-01

2018-06-12

现代农业产业技术体系建设专项资金资助（CARS-29）

袁全春，博士生，主要从事生物生产自动化研究。 Email：yqcmail@qq.com

徐丽明，教授，博士生导师，主要从事生物生产自动化研究。Email：xlmoffice@126.com

袁全春，徐丽明，邢洁洁，段壮壮，马 帅，于畅畅，陈 晨. 机施有机肥散体颗粒离散元模型参数标定[J]. 农业工程学报，2018，34(18)：21－27. doi：10.11975/j.issn.1002-6819.2018.18.003 http://www.tcsae.org

Yuan Quanchun, Xu Liming, Xing Jiejie, Duan Zhuangzhuang, Ma Shuai, Yu Changchang, Chen Chen. Parameter calibration of discrete element model of organic fertilizer particles for mechanical fertilization[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(18): 21－27. (in Chinese with English abstract)

doi: 10.11975/j.issn.1002- 6819. 2018. 18.003 http://www.tcsae.org