近59年合肥气温特征分析及其未来变化趋势预测

罗 悦， 俞文政

(南京信息工程大学 应用气象学院，江苏南京 210044)

引 言

据IPCC第五次评估报告，1880—2012年全球地表平均温度已经升高了0.85℃，并且在过去30a增加幅度不断加大[1]。2015年第三次国家气候变化报告指出，中国从1909年到2010年温度升高了1.52℃，远高于全球平均增幅，且我国地表温度分布呈现由北向南逐渐升高趋势[2]。全球性气候变暖对生态系统和社会经济发展带来了严峻挑战。因此开展区域气候变化的评估和分析，对于国家和地方制定相关对策具有重要意义。

对局部区域温度变化的监测，可作为正确理解和评估区域范围温度变化的参考依据[3]。尽管目前有学者对合肥区域的温度变化进行了研究，但针对长时间序列的温度变化趋势和周期特征分析较少，并且很少有深入到季节尺度的研究。

合肥市(30°57′N-32°32′N，116°41′E-117°58′E)是安徽省会城市，地处华东地区，位于长江淮河之间，横跨安徽32°N南北温度分界线[4]。气候属于亚热带季风性湿润气候，四季分明，年均温15.7℃。1978年改革开放之后，合肥城市化进程的不断加速使得合肥市热岛效应日益明显，对市区温度变化产生一定影响，进而带来一系列环境压力。在全球气候变暖大背景下，结合合肥区域特点进行长时间序列的温度特征分析，对于充分利用地区热量资源和研究合肥的城市热岛、经济社会发展，以及农业生产和减缓气候变化带来的城市环境压力都具有科学指导意义，同时也为长三角城市群大区域温度变化特征研究提供参考价值。

本文选取59年长时间序列，时间横跨1978年改革开放前后，分析年代尺度上温度的趋势和周期变化，揭示温度变化规律。在利用线性回归进行温度趋势变化分析的基础上，通过小波提取出周期特征结合R/S分析法，研究全年和四季温度变化特征，对合肥未来温度变化趋势进行预测，这将对全面认识该区域温度变化特征以及探讨其与全球气候变暖大背景的联系有一定现实意义。

2 数据及方法

2.1 数据及订正

合肥国家气象基本站(区号58321)温度数据最早记录于1953年，先后依次在合肥小南门外、芜湖路、巫大岗和骆岗4个地方建站，历经3次迁站，1955年1月迁到芜湖路(海拔高度23.6m，31°53′N，117°15′E)，1979年1月迁到史河路(海拔高度27.9m，31°52′N，117°14′E)，2004年1月迁到骆岗(海拔高度27.0m，31°47′N，117°18′E)，其中后两次都是由城区迁往郊区，气温序列存在不连续性，需要对温度资料进行均一性订正。

郭守生等[5]通过对比研究发现逐步多元线性回归订正效果优于差值法、一元线性回归和综合订正法。故利用连续t检验[6]，在合肥周边气象台站选取气候环境相似、地理位置相近且没有显著非均一现象的六安、巢湖和寿县气象台站1957—2015年逐月平均温度数据作参考[7]，利用逐步多元回归法，将三个参考站1957—1978年逐月平均温度数据与位于芜湖路时期的合肥台站均温数据建立多元线性回归方程，结合方程与参考台站1979—2015年逐月平均温度数据，订正合肥后两次迁移的台站数据，并对订正结果进行连续t检验，发现统计量均没有超过α=0.01水平临界值，故最终得到完整均一的合肥市区59年气温资料。将订正后的冬、夏两季平均温度值与未订正序列均值进行对比，发现订正后1979—2015年冬夏两季平均温度同比订正前分别升高0.08℃和0.03℃，故合肥气象台站迁移导致温度有细微降低倾向。本文数据来源于中国气象数据网(data.cma.cn)。

2.2 方 法

本文采用t检验法进行参考台站温度序列的均一性检验，可以用来检验两组数据的均值是否有显著差异，其检验统计量为[5]

(1)

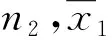
本文采用复数形式的Morlet小波作为母函数，用小波系数模来判定周期大小以及时域分布，消除了实型小波变换系数判定时产生的虚假振荡[8]。小波变化系数正值对应着偏多时期，负值对应着偏少时期，系数值越大表示变化越显著，同时变化系数值正负转折点对应着突变点[9，10]。为了进一步确定主要周期，利用小波方差图进行检验，方差图峰值处时间尺度即对应着气候序列主要变化周期[11]。同时利用线性回归进行温度趋势变化分析，结合Mann-Kendall方法，滑动t检验和累积距平法，综合进行突变检验[12]。R/S分析法是英国学者Hurst于1951年提出，并经Mandelbrot和Wallis进一步补充完善，发展成为研究时间序列的分形理论[13]，可以利用Hurst指数对温度时序进行持续性分析，并结合Morlet小波分析来预测未来温度变化趋势[8]。

R/S分析法主要原理如下[8，13]：

对于一个时间序列{ξ(t)}，t=1,2，…，对于任意正整数τ≥1，定义该时间序列均值为

(2)

累积离差为[8，13]

(3)

极差为[8，13]

(4)

Hurst利用的标准偏差为[8，13]

(5)

Mandelbrotetal证实了Hurst的研究，并得出了更广泛的指规律，即R/S=(τ/2)H，式中，H称为Hurst指数[8，13]。H值即双对数坐标系(Inτ，InR/S)中用最小二乘法拟合所得到的直线的斜率，对应于不同大小的Hurst指数H[13]。

不同的Hurst系数H(0

(1)H=0.5，表明各项气候要素之间是完全独立的，相互不依赖；

(2)0.5

(3)0

综上利用Hurst指数值来揭示气候时间序列的趋势性成分，进而判断未来气候的趋势变化。

3 结果分析

3.1 温度变化趋势和突变分析

结合图1和表1，得出合肥地区59年来温度总体呈现平缓波动到显著增温的变化趋势。年均温增温倾向率为0.205℃/10a(通过0.01水平的显著性检验)，改革开放之前22年间年平均温度平稳波动，改革开放

图1 年和四季平均温度趋势变化及突变图

之后1979—2015年温度显著升高，增温速率达到0.391℃/10a(通过0.01水平的显著性检验)，1978年之后的偏暖年份(温度距平值大于0℃)有22个，占59年来偏暖年份的85%。在季节变化中，春季增温倾向率最大，为0.37℃/10a，其次是冬季，增速为0.255℃/10a和秋季为0.17℃/10a，夏季增温最不明显，仅为0.023℃/10a。除夏季，其余季节均通过了0.01水平的显著性检验，可见春季对年均温的增温贡献最大。

年平均温度在1993年发生了0.88℃的增温突变，相对于突变前温度平均值增幅为5.63%。就季节温度突变，冬季最早于1990年发生了1.01℃增温突变(增幅为27.11%)，其次为春季(增幅10%)、秋季(增幅4.72%)均在1993年发生了1.52℃和0.79℃的增温突变，冬季温度突变最早发生且突变幅度最大。

表1 平均温度回归系数表

注:**为通过0.01水平上的显著性检验

3.2 温度主周期分析

3.2.1 小波系数实部及模分布图 图2和图3展示了温度在不同时间尺度上Morlet小波系数实部及系数模分布图。在小波系数实部分布图中加粗实线表示0值点(对应可能突变时间点)，正负小波系数实部分布图，实线表示正相位(实部大于等于0)，虚线表示负相位(实部小于0)，正负相位的交替变化表示温度上升和下降交替出现的变化特征。模分布图中模对应数值的大小代表特征时间尺度信号的强弱分布。

从图2(a)和图3(a)观察到年均温4～7a、14a时间尺度上存在明显波动变化,正负相位交替出现。在14a中长时间尺度变化上，温度变化共出现3次完整正负交替的准振荡，14a周期变化在1960—1980年间强度较高，振荡中心在1970年，自1980年之后14a时间尺度周期振荡强度开始减弱，4a时间尺度周期振荡自1977年开始增强，存在两个振荡中心分别是1980和1995年，2000年之后4a尺度周期振荡逐渐减弱，7a时间尺度变为主要振荡周期，振荡中心在2010年；其中1993年在14a时间尺度上是温度增暖转折点，与前文分析的年均温突变时间保持一致。对于45a时间尺度的波动变化，由于时间序列有限，可能是虚假周期，不给予讨论。

由图2、3的(b)(c)(d)(e)观察四季温度周期变化特征。春季在1978—2000年主要存在4a周期振荡，存在两个振荡中心分别是1982年和1998年，2000年之后周期振荡主要集中在7a时间尺度，历经两次完整正负交替的准振荡，振荡中心在2008年；夏季在整个研究时间域内存在3-7a的正负交替周期振荡，7a时间尺度振荡中心位于1970年，1978年之后主要为3a时间尺度周期振荡，且存在3个振荡中心分别是1980年、1998年和2012年；秋季在1957—1980年出现两次11a时间尺度的负正周期振荡，振荡中心在1968年，1980—2006年以4a周期振荡为主；冬季在整个研究时间域内均存在4a时间尺度周期振荡，同时在1960—1990年还存在两次14a时间尺度正负交替周期准振荡，振荡中心为1975年。

3.2.2 小波方差检验 图4为全年和四季Morlet小波方差图，反映了波动的能量随尺度的分布，进而确定温度变化主周期。由图4(a)，根据小波方差峰值对应的时间尺度，可以看出，全年小波方差的主要峰值分别出现在尺度为4～7a、14a处，45a时间尺度对应方差值最大，但由于时间序列长度限制，可能为虚假周期，故不予考虑，故4～7a短时间尺度为第一主周期，14a中长时间尺度为第二主周期。就四季而言，春季平均温度周期振荡以7a为第一主周期，4a为第二主周期；夏季以3～7a时间尺度为第一主周期振荡，秋季以4a为第一主周期、11a为第二主周期振荡，冬季均温周期振荡以4a为第一主周期，14a为第二主周期，四季平均温度周期振荡均以3～7a短时间尺度为第一主周期，秋、冬两季以15a左右时间尺度为第二主周期，符合全年的短周期振荡为主，中长周期振荡为辅的变化规律。

根据小波系数的实部分布图、模等值线图和小波方差图的结果再结合表2得出：4～7a短时间尺度为合肥地区平均温度振荡第一主周期，同时全年和秋冬两季还存在11～14a中长时间尺度的第二主周期。就全年和秋冬两季来分析，11～14a时间尺度周期变化在20世纪50年代末到80年代末信号较强，振荡明显，80年代之后则逐渐显现出4～7a时间尺度的周期变化特征；春夏两季3～7a的短周期振荡存在整个时间域内；根据温度交替变化的周期特征可以预测合肥地区温度未来将继续处于增温的大趋势，2015—2022年温度将继续升高。

图2 Morlet小波变换系数实部时频分布图 图3 Morlet小波变换系数模态分布图

Fig.2 Real part time-frequently distribution from Fig.3 Modulus time-frequently distribution from Morlet wavelet transform coefficients Morlet wavelet transform coefficients

图4 小波方差分布图Fig.4 Wavelet transformation variance

3.3 未来温度变化预测

表2 全年和四季平均温度振荡主周期

注：*表示主周期

利用Hurst指数值揭示合肥温度变化状态以及持续性。对In(R/S)与In(time)进行一元线性回归，得到Hurst指数。根据合肥全年和四季59年来温度变化回归系数，得出温度的历史变化趋势，并结合Hurst指数进一步预测未来温度变化趋势。

利用Morlet小波分析得出合肥地区平均温度主要存在7a左右的周期振荡，因此在Hurst指数预测未来温度变化趋势的基础上，结合全年和四季的线性回归方程计算合肥地区下一个主周期振荡后(即7a时间尺度)的温度变化幅度，分析结果如表3所示。由表3可以看出，不管是全年还是四季的Hurst指数值均大于0.5，甚至达到0.9，这说明平均温度变化趋势具有很明显的Hurst现象，也就是合肥地区未来平均温度延续过去温度变化趋势的可能性很大，结合全年和四季温度回归系数为正值，升温-降温循环交替的周期变化特征，可以综合得出合肥地区未来一段时间内平均温度将会继续升高。

根据不同时间段指标温度序列的历史变化趋势以及对应的Hurst指数，得出以下预测：就59年来的年平均温度而言，未来年平均温度预计会保持升高态势，且2016—2022年温度将继续升高0.14℃左右；就季节而言，除夏季会保持平均温度细微升高的状态之外，冬季、春季、秋季未来温度均保持之前较为明显的升温趋势；春季、冬季、秋季和夏季在今后7a增温幅度由大到小依次为0.26℃，0.18℃、0.12℃和0.02℃。

表3 基于Hurst指数、线性回归趋势系数的合肥未来温度趋势判断

注：R2为In(R/S)与In(time)的一元线性回归方程的判定系数

4 结论与讨论

合肥1957—2015年年平均温度总体呈现升高趋势，增温速率为0.205℃/10a，低于同期的全国平均值0.25℃/10a[14]。但是应该注意到合肥年平均温度在20世纪70年代末之前发生的变化微乎其微，增温速率为0.08℃/10a，没有通过显著性检验，但是在20世纪70年代末之后增温十分显著，增温速率为0.391℃/10a，前后增温速率相差5倍，温度变化明显。一方面是由于近年来气候变暖的大背景趋势，另一方面由于1978年改革开放之后合肥城市化进程高速发展，城市化所带来的热岛效应使得局部温度升高，这也与刘玲等[15]得出的合肥市热岛效应1975年以来逐渐加强，甚至在1989年之后呈直线上升的结果相吻合。不同季节也呈现出不同程度的变暖趋势，春季增温速率最大，其次是冬季和秋季，夏季增温最不显著，这表明增温主要表现在低温的增加而不是高温的上升。与长江三角洲纬度相近其他城市化进程快速发展的城市比较发现，温度变化趋势基本保持一致，增温趋势也主要集中于改革开放之后[16，17]。增温突变基本发生于20世纪90年代初，季节突变冬季最早于1990年发生，春季、夏季的突变时间与年平均温度突变时间保持一致，均发生于1993年。春季对年均温的增温贡献最大，冬季突变幅度最大。

利用Morlet小波和R/S方法分析合肥近59年温度变化特征发现：(1)全年和四季均以4～7a短时间尺度为第一主周期，同时全年和秋冬两季还以11～14a中长时间尺度为第二主周期；(2)合肥全年和四季的Hurst指数均大于0.5，有的甚至达到0.9以上，表明温度时间序列存在明显的赫斯特现象；(3)根据回归系数得出59年来平均温度变化趋势，结合Hurst指数值和温度周期变化特征，推测合肥未来温度仍会持续升高，同时利用回归方程计算出全年和春、夏、秋、冬四季在合肥地区下一个主周期振荡后的温度将分别增加0.14℃、0.26℃、0.02℃、0.12℃和0.18℃，温度的持续升高会对城市居民生存环境和可持续发展产生影响，因此需要引起高度关注。

综上分析，合肥在1957—2015年平均温度总体处于升高状态，地区增温突变主要发生在20世纪90年代初，主要存在4～7a和11～14a的振荡周期，结合周期振荡特征和Hurst指数推测合肥未来温度将会继续升高，与CMIP5预测的未来大增温背景保持一致[18]。