基于截断误差的改进脉冲星导航观测方程

许强， 王宏力， 何贻洋， 由四海， 冯磊

(火箭军工程大学导弹工程学院, 西安 710025)

X射线脉冲星是宇宙中高速旋转并周期性地辐射电磁脉冲的中子星。由于具有高度稳定的旋转周期，使得脉冲星所辐射脉冲的周期及轮廓具有较强的不变性和较高的可识别性。X射线脉冲星导航系统就是利用其稳定的X射线脉冲信号作为观测量进行航天器导航的系统，它具有隐蔽性高、自主性强、抗干扰性好等优点。近年来关于X射线脉冲星导航的相关研究也日益深入。美国国防高等研究计划局早在2004年就已经正式提了X射线脉冲星导航计划——XNAV计划，并于2005年开始研制[1]，欧洲航空局也在2005年制定了类似的“深空探测器脉冲星导航研究(deep space vessel pulsar navigation study)”计划。后续俄罗斯、日本等也都相继开展了相关的研究项目。中国在2016年11月10日于酒泉卫星发射中心成功发射了第一颗脉冲星导航试验卫星XPNAV-1[2]。

X射线脉冲星导航的测量原理是根据航天器与太阳系质心(SSB)在脉冲星方向的多普勒延迟得到航天器在SSB坐标系中的状态[3]。观测量是脉冲到达航天器与SSB的时间差或其与光速的乘积。但在宇宙中，脉冲信号的传播会受天体运动、相对论效应等的影响而产生变化，也就在观测方程之中引入了高阶项[4]。在当前研究中，扩展卡尔曼滤波(EKF)算法因具有工程实现简单、算法成熟、实时性好等特点而得到广泛应用。但是在X射线脉冲星导航中应用EKF算法时却常常因为线性化需要而忽略观测模型高阶项的影响[5-8]，这实际会给导航结果带来较大截断误差甚至导致发散。这些高阶项的变化大多是慢时变的，短时间内可以认为是常值并进行补偿，长时间来看却有着较大的变化波动。对于X射线脉冲星导航在深空探测器、长期在轨卫星上的应用影响较大，有必要通过在线估计的方法予以补偿。

针对以上问题，本文以地球长期在轨卫星为背景，通过对高阶项的产生机理及数值量级进行仿真分析，提出一种改进的线性观测方程。该方程既不需要额外增加状态量，也满足以EKF为基础的各种拓展滤波算法应用于脉冲星导航时对观测方程线性化的要求。并通过对比不同时段X射线脉冲星导航系统的仿真结果,证明了该方程的有效性。

1 典型脉冲星导航空间方程

1.1 状态方程

X射线脉冲星导航的状态方程是基于航天器在地球质心惯性系中的动力学方程建立起来的。状态量选为航天器在地球质心惯性系中的位置和速度。在考虑二阶带谐项时，其状态方程为[9]

(1)

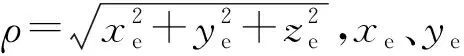
则可将其状态方程简写为

(2)

式中：w(t)为系统噪声矩阵，且

(3)

1.2 观测方程

本文X射线脉冲星导航中，观测量选用X射线脉冲信号到达航天器和SSB的时间差Δt与光速c的乘积。如果不考虑其他物理效应的影响，其简化的观测模型如下[10]：

cΔt(i)=nirsat

(4)

式中：cΔt(i)为第i颗脉冲星对应的观测量;ni为第i颗脉冲星的方向矢量，下标i为脉冲星的编号；rsat为卫星在SSB坐标系中的位置矢量。由于状态方程中使用的状态量是航天器在地球质心惯性坐标系中的位置和速度，所以可将rsat表示为rsat=rE+r，rE为SSB坐标系中地球的位置，可以通过地球星历预报得到,r为卫星在地球质心坐标系的位置矢量。所以，X射线脉冲星的观测方程可以简写为

(5)

2 观测模型高阶项分析

如图1所示，简化的线性观测模型中仅有几何延迟项，即nrsat=cΔt，n为脉冲星的方向矢量。脉冲信号在宇宙中传播时理论上能够对传播时间产生影响的还有相对论效应、色散延迟等[4]。但是考虑到当前光子到达时间的测量精度在微秒量级，理论精度应达到10-8s，所以能够产生截断误差的因素主要考虑地球周年运动导致的周年视差效应和恒星引力场作用下光线弯曲产生的引力延迟效应[11]。

OS-XSYSZS—太阳质心坐标系; OSSB-XSSBYSSBZSSB—太阳系质心坐标系; b—太阳质心到SSB的矢量； rE—地球在太阳系质心坐标系中的位置。图1 脉冲星导航基本原理Fig.1 Basic principle of pulsar navigation

2.1 周年视差效应

假设观测者在地球上对恒星进行观测，由于地球的公转，恒星在天球上的位置也会发生改变。以太阳上观测的恒星在天球上位置作为其平均位置，从地球上观测的位置为其实际位置。由于地球围绕太阳公转，2个位置会存在一定的偏差，也就是所谓的恒星周年视差。周年视差在日地连线(太阳与地球连线)同星日连线(脉冲星与太阳连线)垂直时达到极大值，如图2所示。

理论上而言，被观测恒星距离太阳的距离越远，周年视差效应会越不明显，所以脉冲星导航中此项的时间量也是一个很小的数值。但是在X射线脉冲星导航的解算过程中，该项会直接与光速相乘，而且由几何原理可知，该项产生的误差投影到3个坐标方向上之后，各方向误差的代数和会变大，如式(6)所示:

(6)

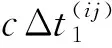
在短时间内周年视差效应引起的偏差变化不明显，但是一年内的变化幅值却比较大。如果X射线脉冲星导航系统长时间的运行，那该项的影响必须予以考虑。关于周年视差效应在X射线脉冲星观测中的影响的具体推导属于天文学范畴，在此直接由式(7)给出[11-12]：

图2 周年视差效应原理Fig.2 Principle of annual parallax effect

(7)

式中：D0为脉冲星距离SSB的距离。

2.2 引力延迟效应

引力延迟效应也称Shapiro效应，是在太阳系内验证广义相对论的4个经典试验之一。它是指当射电或者光信号经过大质量的天体时，受天体重力场的影响其速度方向会发生变化，传播的行程增加，传播到目的地或往返的时间也会因此增加，如图3所示[13]。所以如果观测者同样在地球上，当地球位于星日连线上时，引力延迟效应最明显；当地球位于星日连线的延长线上时，引力延迟效应相互抵消，影响效果最小。

引力延迟效应对导航结果的影响同周年视差效应相同，在此不再赘述。根据天文学知识，可以得到太阳系内天体引力延迟效应的总和为[14]

(8)

由于太阳系内太阳质量最大，产生的引力延迟也就最大，约为微秒量级[15]。而其他天体的引力延迟均不大于10-8s，所以受光子测量精度影响可以不予考虑。若仅考虑太阳引力场的作用，则式(8)可以简化为

(9)

式中：Msun为太阳质量。

图3 引力延迟效应原理[13]Fig.3 Principle of Shapiro effect[13]

2.3 数值分析

通过以上分析，能够产生截断误差的主要为地球运动的周年视差效应和太阳的引力延迟效应。利用STK9.0版本软件按照表1中的轨道参数分别仿真产生一天及一年内的高精度HPOP卫星运行轨道，并以表2[16]中B1821-24脉冲星的参数为例计算式(7)和式(9)的结果，太阳质量Msun=1.989 1×1030kg，万有引力常数G=6.67×10-11m3·kg-1·s-2。一天和一年内高阶项变化情况结果分别如图4和图5所示。

通过分析可以发现：周年视差效应和太阳引力延迟效应的变化幅度明显，最大与最小值能相差10倍之多，一年内周期变化明显。最大值最小点计算的结果与第2.1节及2.2节的理论分析相吻合。

表1 轨道参数

表2 B1821-24脉冲星的参数[16]

注：1 kpc=3.08×1019m。

图4 一天内高阶项变化情况Fig.4 Variation of higher order terms in a day

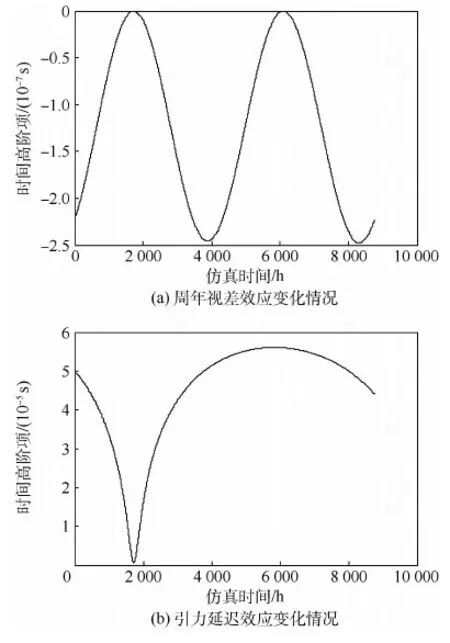
图5 一年内高阶项变化情况Fig.5 Variation of higher order terms in a year

3 线性观测方程的改进

由于滤波周期内卫星绕地球的运动相对于卫星到SSB的距离|rsat|来说非常小，所以结合式(7)，在k时刻可对脉冲星导航中的周年视差效应做如下化简：

(10)

式中：rsat(k-1)为k-1时刻卫星在SSB中的位置；rsat(k)为k时刻卫星在SSB中的位置。

引力延迟效应的影响量级最大，同理也可对k时刻的式(9)进行如下简化处理：

(11)

令

(12)

则将式(11)在k-1时刻对rsat进行一阶泰勒展开：

a1ln(a2+a3rsat(k))=a1ln(a2+a3rsat(k-1))+

(13)

式中：Δ为泰勒展开中二阶以上高阶项。

省略二阶以上高阶项后可得

Δt2≈a1ln(a2+a3rsat(k-1))-

(14)

综上所述，结合式(5)、式(10)、式(12)、式(14)，可将改进的带有高阶项的线性观测方程写为

(15)

4 仿真分析

为验证本文所提出的改进观测方程对导航结果的提高效果，本文利用表1中的数据仿真产生卫星运行轨道。所用的X射线背景流量BX=0.005 ph·cm-2·s-1，探测器面积A=1 m2，脉冲星导航周期为60 s，导航采用B0531+21、B1821-24及B1937+21三颗脉冲星，具体参数见表3[16]。地球引力常数为3.986 004 418×1014N·m2/kg，光速为3×108m/s，重力二阶带谐系数为0.001 082 63，地球赤道半径为6.378 137×106m。本文中脉冲星导航的其他初始条件设置如下：

1) 初始误差为

δx=(1 000 m,1 000 m,1 000 m,20 m/s,20 m/s,

20 m/s)

2)初始误差协方差为

P(0)=diag[1 0002m2,1 0002m2,1 0002m2,

202m2/s2,202m2/s2,202m2/s2]

3) 系统噪声协方差为

式中:q1=8 cm;q2=0.05 mm/s。

4) 量测噪声协方差为

Rk=diag[1092m2,3252m2,3442m2]

通过第2节对高阶项的分析可以得知，假如

表3 导航用脉冲星参数[16]

从卫星上对脉冲星进行观测，在一年中有4个点比较特殊，都是在日卫连线(太阳与卫星连线)与星日连线相共线或垂直时。由于导航的截断误差同时受3颗脉冲星的高阶项变化影响，所以3颗脉冲星高阶项总和的周年变化在脉冲星导航中是有实际影响意义的。

3颗脉冲星高阶项总和的周年变化情况如图6所示。为了验证改进的线性观测方程的有效性，本文选取其最大值和最小值点，即2015年10月17日与2015年12月29日进行仿真运算,仿真结果见图7～图10。同时为了更好地评价算法的估计性能，本文采用均方根误差(RMSE)作为导航误差的计算公式[17]，统计区间为一天中的(900,1 440) min区间，RMSE的表达式为

(16)

式中：Δrk为第k时刻真实的轨道位置与滤波器估计位置之间的距离。

图6 全年3颗脉冲星高阶项总和变化Fig.6 Whole year variation of summation of three pulsars’ higher order terms

图7 2015年10月17日简化线性观测方程估计结果Fig.7 Estimation results of simplified linear measurement equation on October 17, 2015

图8 2015年10月17日改进线性观测方程估计结果Fig.8 Estimation results of improved linear measurement equation on October 17, 2015

图9 2015年12月29日简化线性观测方程估计结果Fig.9 Estimation results of simplified linear measurement equation on December 29, 2015

图10 2015年12月29日改进线性观测方程估计结果Fig.10 Estimation results of improved linear measurement equation on December 29, 2015

为了降低随机因素对结果的影响，将2个线性观测方程分别独立运算50次并对导航结果求平均值，结果信息统计如表4所示。通过运行结果的图表来看，在考虑高阶项的情况下使用简化线性观测方程进行EKF解算时，忽略高阶项影响而产生的较大截断误差已经导致滤波发散，而改进的线性观测方程却仍然能够较好较快地将位置估计误差收敛到250 m以内，速度估计误差2 m/s以内，并且在高阶项的最大值点与最小值点的位置估计误差仅相差2.6 m，速度误差仅相差0.038 2 m/s。方程对高阶项的变化表现出较好的鲁棒性。通过运算时间反应运算量，在60 s更新周期的条件下，用配置i3处理器的台式计算机运行2012A版本MATLAB进行导航解算，2种方程进行一天内的导航解算，总运行时间分别为2.054 4 s和1.749 0 s,平均每次计算仅相差0.000 2 s。

表4 2种观测方程的估计误差

5 结 论

本文提出一种适用于脉冲星导航的改进线性观测方程。该方程包含了脉冲星观测模型中会对观测量造成较大高阶截断误差的周年视差效应和引力延迟效应。仿真结果表明：

1) 在考虑周年视差效应和引力延迟效应影响的情况下，简化的线性观测方程在EKF算法中会产生发散，而改进的线性观测方程却能较快的得到250 m和2 m/s以内的位置和速度估计误差。

2) 改进的线性观测方程对高阶项的变化具有一定的鲁棒性。在高阶项变化的最大值和最小值点位置估计误差仅相差2.6 m，速度估计误差仅相差0.038 2 m/s，适合长时在轨航天器的导航解算。