中考数学开放题教学研究

施菊燕

(江苏省南通市如东县实验中学 226400)

一、开放性试题的特点

数学开放题和我们常见的选择题、填空题、计算题、证明题等基本题型不同，更加凸显“开放”这一特征.具体而言，开放型试题的主要特点如下：

1.思维方式不确定性

常规的数学习题都有固定的解题思路，结果也是唯一的.但是，开放性试题具有一般性与不确定性，不存在固定的解题模式，答案也并不绝对是唯一确定的.

2.难度不固定性

数学开放题的难度不固定，学生解答的难度并不绝对.有些开放题考查的是学生的综合思维，本身就不具备思维难度；有些问题需要学生具有完整性的思维能力，在解答过程中需要学生从多个不同的角度.全方位地进行思考，思维不能局限.

3.答案不唯一性

数学开放题考查的重点不是学生能得出最后的答案，更加注重的是学生在解题过程中对知识的合理运用以及认知重构，答案是多种多样的，只求解出一个答案显然就失去了这类试题的实际意义.答案不唯一，说明了这类考题的思维方式、解决方法等都是多样的，学生可以从自己喜欢的角度入手，选择自己最熟悉的思考方式，在学生的解答过程中，老师能考查学生对相应知识点的掌握情况.同时，答案的多样性能激起学生的学习兴趣，保证处于不同学力水平的学生都能积极思考，参与到教学活动当中去.

4.现实性

数学开放题一般都会有问题背景，考查的是学生从实际问题出发进行数学化处理的能力，也就是简单的数学建模思维.在现实问题情境中，学生运用所学的数学知识，解决实际问题，数学运用能了得到了有效的提升.

5.延伸性

数学开放题的另一大特征就是延伸性，在求解过程中往往会衍生出新的问题，或者是发现解决问题的全新角度，这就要求教师引导学生养成正确的问题观，不要一味地强调答案的重要性，要让学生在解决问题的过程中提升思维张力，锻炼思维能力，训练数学知识运用能力.

二、教学策略

数学综合开放题中，条件、方法、结论中的两项是开放的，题目不会给出明确的信息，而是创设一种问题情境，学生需要做的就是补充条件，设计结论，探究该问题的解决方法，具有明确的随机性与不确定性，对学生的思维限制比较小，.在解决综合开放题时，教师要引导学生认真观察与思考，集中分析题目中的有用信息，反向思维，推理结论成立所需的条件.

1.案例展示

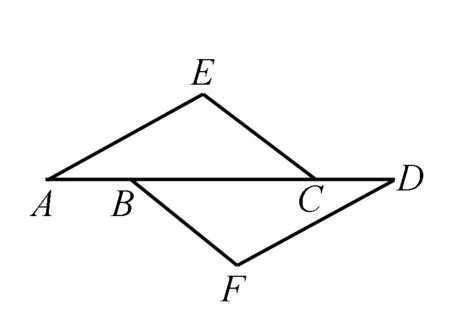
如图所示，在三角形AEC和三角形DFB中，角E与角F相等，点A、B、C、D共线.现有如下三个关系式:

①AE∥DF;②AB=CD;③CE=BF.

请将以上三个条件中的两个作为已知条件，另外一个作为结论，尽可能多地写出正确的命题，并选择一个命题进行证明.

2.思路梳理

(1)如果将①②作为已知条件，③作为结论，得到的命题为真命题，可以利用“角-角-边”原则证明三角形ACE与三角形DBF全等；

(2)如果将①③作为已知条件，②作为结论，得到的命题为真命题，可以利用“角-角-边”原则证明三角形ACE与三角形DBF全等，进而证明了AC=BD.

3.问题解答

(1)已知AE∥DF，AB=CD，求证CE=BF.

∵AE∥DF,∴∠A=∠D.

∵AB=CD,∴AB+BC=BC+CD,∴AC=DB.

在三角形ACE和三角形DBF中，

∠E=∠F，∠A=∠D，AC=DB，

∴△ACE≌△DBF(AAS).

∴CE=BF.

(2)已知AE∥DF，CE=BF，求证AB=CD.

∵AE∥DF,∴∠A=∠D.

在三角形ACE和三角形DBF中,

∠E=∠F，∠A=∠D，EC=FB，

∴△ACE≌△DBF(AAS).

∴AC=DB,∴AC-BC=DB-BC,

∴AB=CD.

4.反思点评

本题属于条件和结论都开放的试题，对学生的几何知识点整合能力进行了考查，与传统的全等三角形知识点考查不同，这一题型鼓励学生进行探究，旨在让学生从多个角度看待问题，多策略地思考问题，多方案地解决问题，培养和提升学生的创新意识以及自主探索能力.

经过教学实践，笔者发现科学的开放性试题能让学生的思维更加活跃，有利于学生学习能力以及数学思维能力的培养，同时也能提升学生的问题解决能力.各地的中考中已经开始出现这类新题型，可见这是未来初中数学教学的一大趋势，也是新课程改革的要求，提倡学生的综合发展.