小间距桥梁承台施工对运营地铁隧道的影响分析

谢春华

（深圳市前海深港现代服务业合作区管理局，广东 深圳 518054）

0 引言

新建结构物在既有结构物一定影响范围内进行施工，对既有结构物产生一定不利影响的工程称之为近接工程[1]。目前，国内由于城市轨道交通日趋完善，地铁隧道工程不可避免地会近接其他构筑物施工，难免对既有构筑物产生不利影响，针对这一问题，国内外很多学者进行了相关研究。如：李光伟[2]运用ABAQUS建立三维有限元模型，从铁路桥桩基位移、倾斜及内力的变化方面模拟盾构隧道开挖对临近桥梁的不利影响；贺美德、刘军等[3]以北京地铁盾构区间隧道近距离侧穿高层建筑为背景，采用有限元计算和现场监测相结合的方法，对新建隧道施工所引起的邻近高层建筑物的结构沉降、基础倾斜进行深入研究。但少有新建桥梁近接既有运营地铁隧道施工的工程与研究，如路飞、郑刚[4]通过三维有限元数值模型模拟立交桥桥墩桩基的成孔施工、运营期桩基承担荷载在土中产生的应力扩散对既有隧道结构与轨道变形产生的影响，并分析了单个承台桩基础及考虑多个承台桩基础叠加效应对邻近既有隧道的影响规律。所以研究如何合理确定新建桥梁施工对既有运营地铁隧道的影响具有十分重要的理论研究和现实意义。

鉴于此，本文以深圳前海合作区新建景观桥梁上跨运营地铁隧道为背景，通过M IDAS/GTS建立三维有限元模型进行数值计算，对既有地铁隧道变形与受力进行研究。

1 工程概况

该项目为前海合作区规划中的10号景观桥，桥位位于地铁1、5和11号线保护范围内，目前三条地铁线均处于运营中，5、11号线位于景观桥的正下方，1号线位于该工程的东侧。景观桥和地铁的相互关系如图1所示。

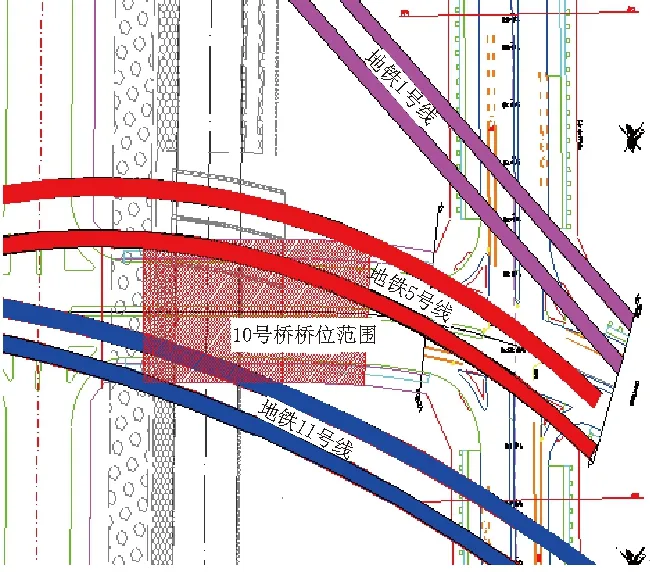
图1 新建隧道与既有隧道断面图及交叉段平面图

1、5和11号线均已经建成，均为双线行车，采用盾构施工，盾构隧道采用圆形截面，结构外径为6 m。

1号线位于景观桥东侧，且桩基与1号线结构边缘最小净距为 31.7 m；5号线与景观桥工程范围相交，隧道顶标高为-6.38～-7.16 m，承台基坑底部距离地铁结构外边缘距离最小为4.625 m；11号线与景观桥工程范围相交，隧道顶标高为-10.05～-11.94 m，承台基坑底部距离地铁结构外边缘距离最小为8.95 m。

该地段分布的地层主要有人工填土层、第四系海相沉积层、第四系冲洪积层及残积层，下伏基岩为燕山晚期花岗岩及加里东期混合岩。场地地下水主要为松散孔隙潜水和基岩风化裂隙水，人工填土与地表水及大气降水联系紧密，地下水的补给条件好，但地下水离散性大，场地地下水相对较贫乏；基岩裂隙水水量较小，含水层通道呈网络状，具各向异性。

2 数值模拟分析

2.1 有限元模型的建立

隧道开挖引起的应力重分布只在一定范围内进行，因而计算范围只要合理选取就能保证模拟的精确。经过理论分析与工程实践经验所得，隧道开挖后引起的应力和应变改变范围为3～5倍隧道开挖直径。因此计算边界一般可确定为3～5倍开挖隧道宽度[5]。综合考虑隧道断面大小、与承台基坑间距等后，计算模型几何尺寸分别定为185 m、170 m、45 m，如图 2所示。

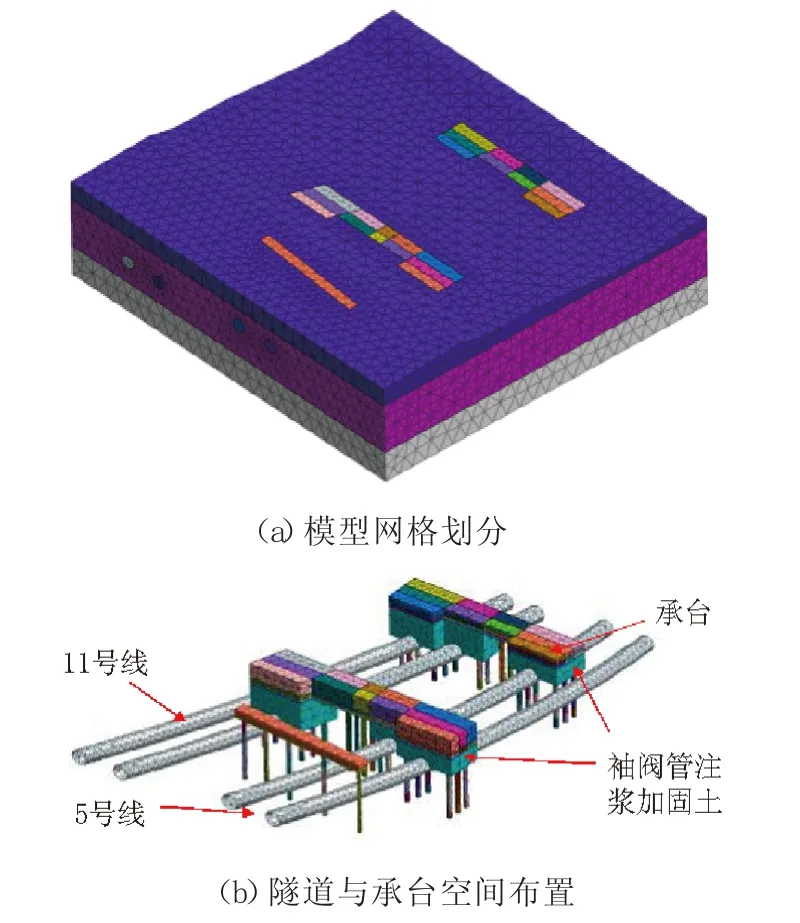
图2 模型网格划分示意图

由于桩基与1号线结构边缘最小净距为31.7m，相对净距大于3D（D为盾构直径6 m），接近程度为不接近，故可忽略对1号线隧道结构的影响分析。

2.2 模型参数的选取

根据岩土工程勘察报告，结合已有工程经验与《公路隧道设计规范》（JTG D70—2004）[6]等相关文献，模型参数取值见表1和表2。

2.3 考察点的选取

由于本文主要研究隧道上方承台基坑的开挖施工对下方地铁隧道的影响，且该项目南北承台基坑相距较远，相互影响较弱，所以本文以南侧承台基坑下方隧道结构为考察点。

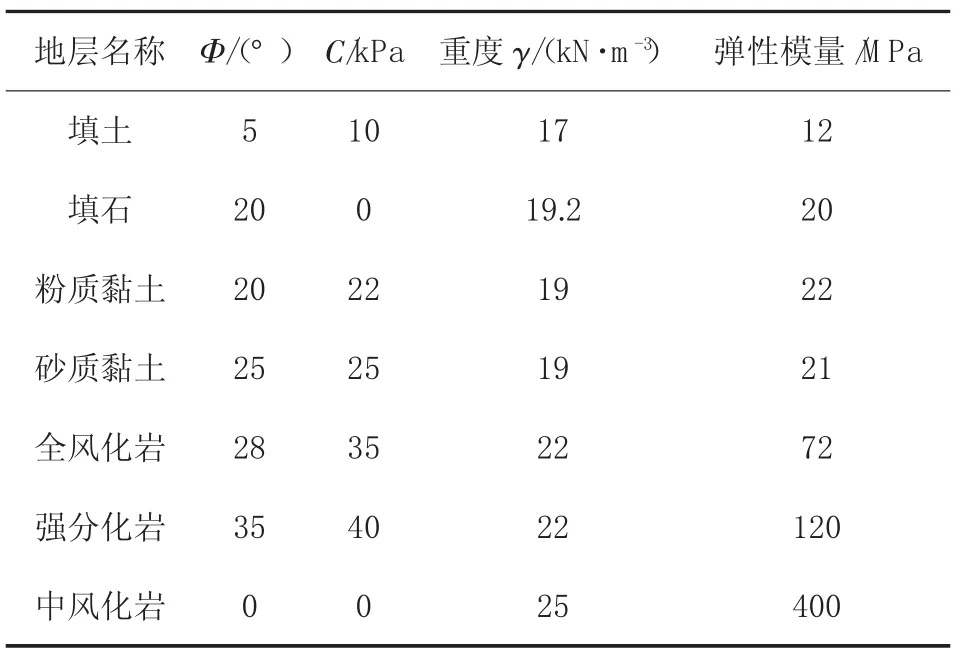
表1 物理力学参数

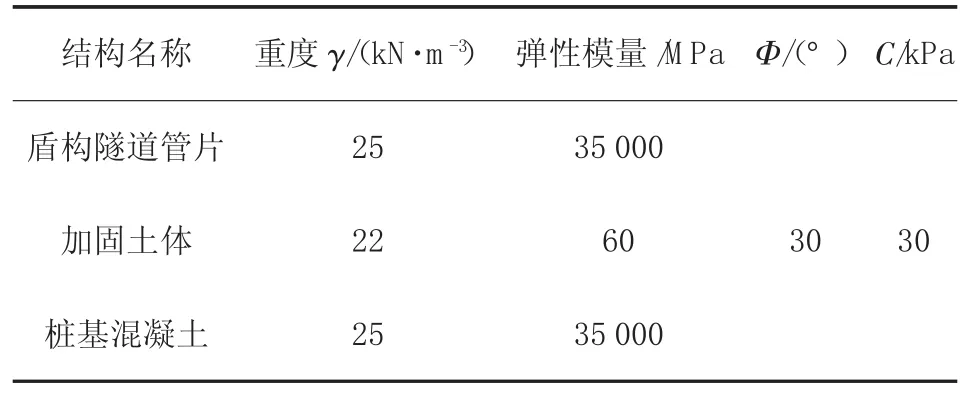
表2 隧道结构参数

2.4 施工模拟与分析工况

在整个10号景观桥的建造施工以及投入使用的过程中，南北承台基坑开挖的施工对既有地铁隧道的扰动影响是明显的，基坑开挖施工顺序的建立是模型分析的关键所在。

如图3所示，该次分析工况先计算初始应力，然后激活南侧管片、桩基与钢支撑，然后E1、F1、E2、F2 后 G1、G2、H 1、H 2 的开挖施工，同理激活并开挖北侧，主要分为40个工况，即40个施工步。

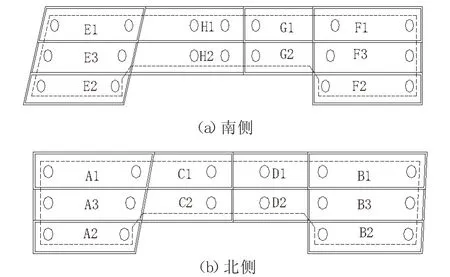
图3 桥梁承台基坑分块开挖平面图

2.5 地铁保护标准

鉴于地铁隧道运营安全的考虑，本文以南侧承台下隧道结构位移、纵向变形曲线的曲率半径与隧道结构附加应力研究分析对地铁隧道的影响：

（1）结构绝对隆起量、沉降量及水平位移量不大于10 m m（包括各种加载和卸载的最终位移量）。

（2）隧道纵向变形曲线的曲率半径R≥30 000 m。

（3）由于建筑物垂直荷载（包括基础地下室）及降水、注浆等施工因素而引起的隧道结构附加应力不大于 10 kPa（1t／m2）。

3 对既有地铁隧道的影响分析

3.1 隧道结构变形

施工过程中会引起既有隧道结构发生隆起变形，必须要保持既有隧道结构变形在控制范围之内。故在施工过程中既有隧道结构最大变形的变化曲线如图4所示。

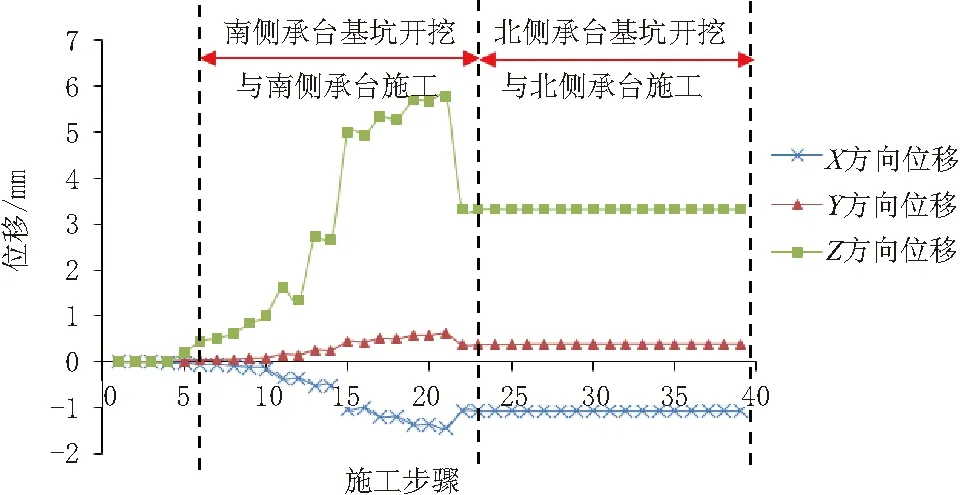
图4 南侧承台下既有地铁隧道最大变形

由图可知，承台基坑的开挖引起隧道结构以竖向位移为主的位移，且随着南侧承台基坑的不断开挖与施工，X、Y和Z方向（X方向为垂直隧道轴线方向，Y方向为隧道轴线方向，Z方向为竖直方向）的绝对最大位移值均逐渐增大，由于北侧承台距考察点间距较大，所以继续开挖北侧承台基坑，隧道各方向的最大位移值均不再增加，地铁隧道的变形已达到最大值。其中，X方向位移最大值为1.44 m m，Y方向位移最大值为0.61 m m，Z方向位移最大值为5.76 m m。隧道各位移的量值小于城市轨道交通保护规范对位移的限值，地铁隧道是安全的。

3.2 隧道纵向变形曲线的曲率半径

隧道纵向变形曲线曲率半径越小，则对隧道结构越不利，因此根据分析可知，隧道纵向变形曲线曲率半径最小值应出现在隧道最大上浮位移值附近，故选取隧道纵向变形曲线最大上浮位移值附近一系列节点，以每三个相邻节点为一组求其曲率半径，取其最小值。曲率半径公式如下：

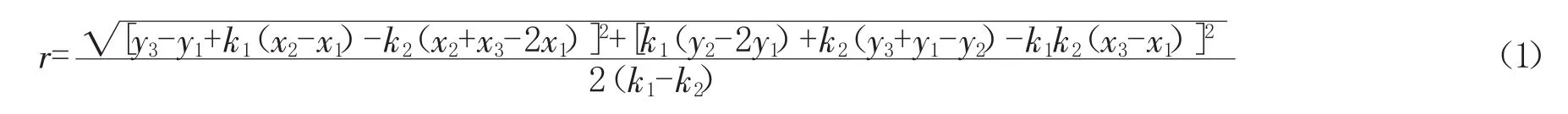
式中：（x1，y1）、（x2，y2）、（x3，y3）分别为试样上标记的三点坐标。

依据上式计算结果见表3。

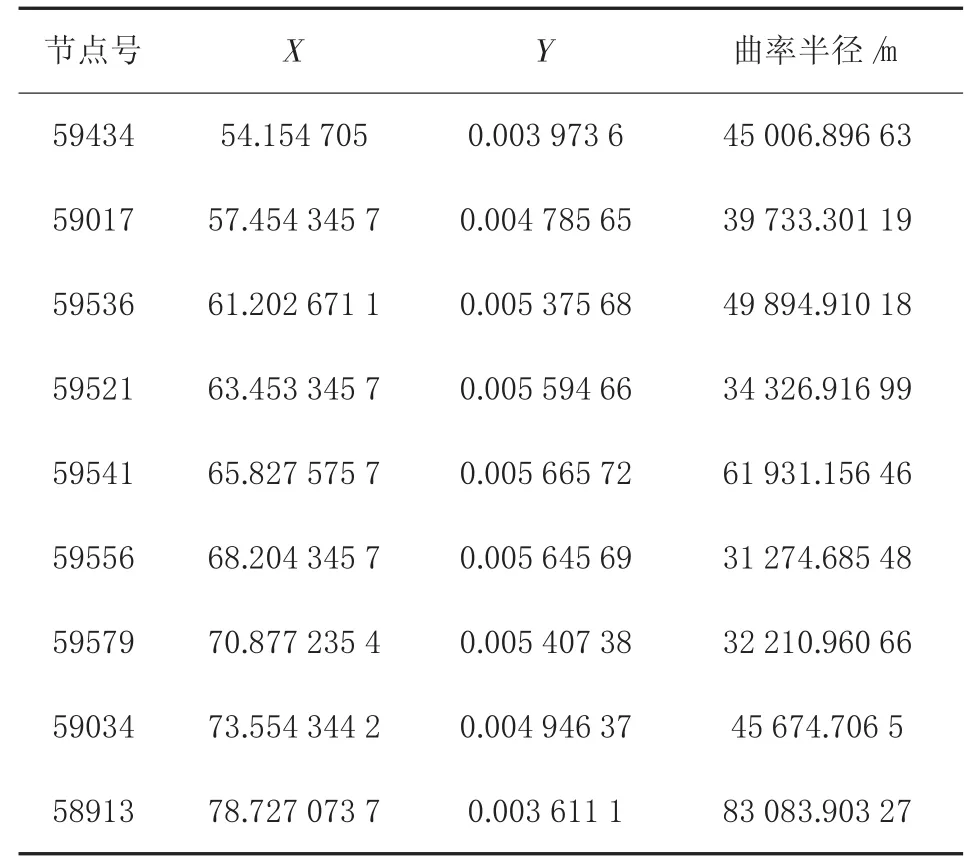
表3 曲率半径计算表

隧道纵向变形曲线曲率半径的最小值为31275m，其值大于地铁结构保护标准规定的30 000 m，满足地铁隧道保护标准。

3.3 隧道结构附加应力

承台基坑的开挖施工会引起隧道结构产生附加应力，并且距基坑越近，隧道结构所受影响越大，故选取南侧承台基坑下方隧道左右两侧与隧道顶部和底部土体分别观测记录隧道结构X于Z方向附加应力的变化，从而分析基坑开挖作用对隧道结构附加应力的影响。

3.3.1 隧道结构X方向附加应力的变化

基坑未开挖前，11号线周围特征点初始值分别为203.61 kPa、207.88 kPa，5号线周围特征点初始值分别为148.44 kPa、145.24 kPa，如图5所示；开挖过程中，11号线周围特征点应力极值分别为202.5 kPa、206.64 kPa，5号线周围特征点的极值分别为146.95 kPa、144.16 kPa，如图6所示。

因此，11、5号线X方向附加应力值分别为-1.11 kPa、-1.24 kPa和 -1.49 kPa、-1.08 kPa。

3.3.2 隧道结构Z方向附加应力的变化

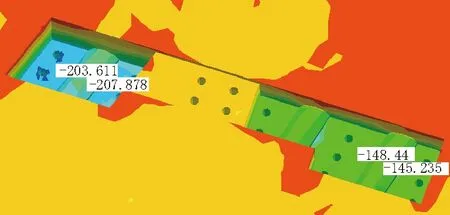
图5 基坑未施工前土体X方向应力初始值（单位：kPa）

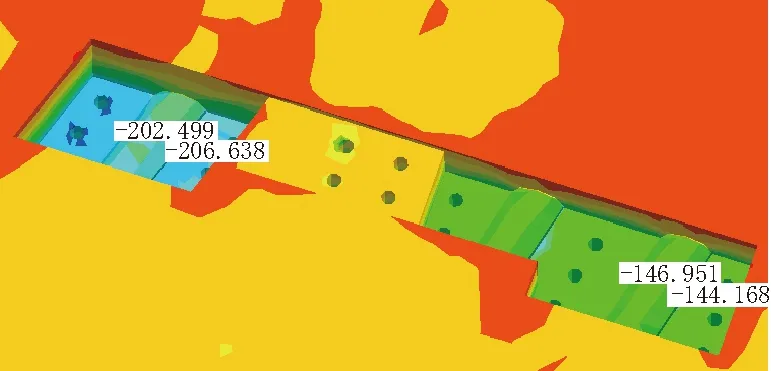
图6 基坑开挖过程中X方向应力极值（单位：kPa）

基坑未开挖前，11号线周围特征点初始值分别为232.69 kPa、350.75 kPa，5号线周围特征点初始值分别为149.62 kPa、281.18 kPa，如图7所示；基坑开挖过程中，11号线周围特征点的极值分别为228.52 kPa、348.75 kPa，5号线周围特征点的极值分别为145.27 kPa、279.83 kPa，如图8所示。

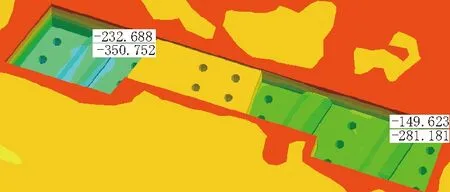
图7 基坑未施工前土体Z方向应力初始值（单位：kPa）

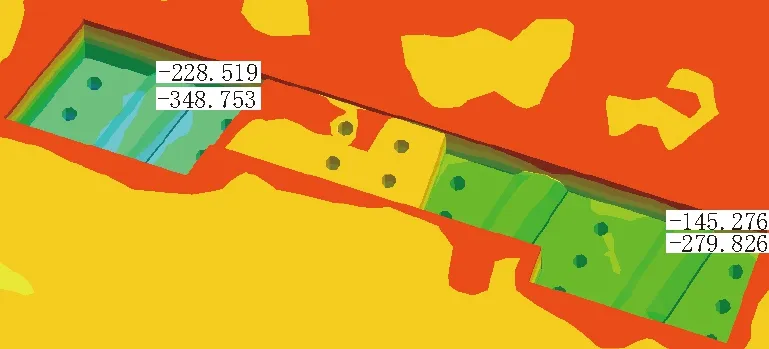
图8 基坑开挖过程中Z方向应力极值（单位：kPa）

因此，11、5号线Z方向附加应力值分别为-4.17 kPa、-2.00 kPa和 -4.35 kPa、-1.35 kPa。

根据上述结果，隧道结构X和Z方向附加应力增量的极值分别为-1.49 kPa和-4.35 kPa，均小于0，表明承台基坑开挖不会引起隧道结构附加荷载的增加，对结构有利。

4 结语

该次分析利用大型有限元软件M IDAS/GTS，根据地质资料及上述基坑支护方案，建立了三维地层模型及三维基坑支护模型，对承台基坑开挖引起的既有隧道结构的变形进行了计算，得到如下结论：

（1）随着地铁隧道上方承台基坑的开挖，隧道结构变形逐渐增大，且与轴线垂直向位移（X方向）最大值为1.44 m m，轴向（Y方向）位移最大值为0.61 m m，竖向（Z方向）位移最大值为5.76 m m。根据《城市轨道交通结构安全保护技术规范》（CJJ/T 202—2013），盾构地铁隧道各位移的量值小于城市轨道交通保护规范对位移的限值，在隧道结构位移控制方面，采用上述地铁保护方案是较为安全的。

（2）隧道纵向变形曲线曲率半径、隧道相对变曲以及隧道管片X和Z方向特征点附加应力增量均满足地铁隧道保护标准。

关于类似的文献资料和工程实践资料相对较少，模拟效果也有待于进一步验证，因此建立在工程实测资料基础之上并且符合实际情况的计算模型是亟须解决的问题，这样模拟结果才能指导近接工程的设计与施工。