不同条件下两种方法计算雨水设计流量的比较

肖君健

（武汉市规划设计有限公司，湖北 武汉 430014）

0 引言

雨水设计流量是确定城市雨水管渠规模的重要指标，其计算方法及取值的合理性直接关系到工程的经济性和安全性。在城市雨水管网设计时，通常采用推理公式法来计算最大设计流量。随着计算机技术的发展和产汇流理论的逐渐完善，数学模型如 SW M M 、Di gi t al W at er、Inf oW orks CS、M IKE URBAN等被应用于计算雨水管网的设计流量。2016年版《室外排水设计规范》（以下简称新版规范）中，补充规定了推理公式法的适用范围：“当汇水面积超过2 km2时，宜考虑降雨在时空分布的不均匀性和管网汇流过程，采用数学模型法计算雨水设计流量。”根据新版规范，城市雨水管渠雨水设计流量的计算存在推理公式法和数学模型法两种并列方法[1-2]，并指出当汇水区面积较大时，推理公式法具有一定的局限性。推理公式法的计算结果相对数学模型法是偏大或是偏小，除了受汇水区面积大小影响外，两种方法计算结果是否还受汇水区水文形状、地面集水时间t1取值等因素的影响，还有待研究。因此有必要开展数学模型法和推理公式法在不同汇水区面积、汇水区形状系数等条件下的比较分析，以期为城市雨水管渠设计流量的计算方法选择及其合理取值提供参考。

1 数学模型的选取

随着新版规范的发布及全国城市排水防涝规划编制的开展，数学模型如EPASW M M、Di gi t al W at er、Inf oW orks CS、DH I M IKE 等被广泛应用于模拟城市暴雨径流过程。其中，EPA SW M M模型是由美国环境保护署推出的基于水文水动力学的一维分布式城市暴雨径流管理数学模型，可用于模拟降雨地表产流、地表汇流、管网水动力学传输过程，其产汇流理论和计算引擎被Di gi t al W at er、M IKE SW M M、XP SW M M、PC SW M M 等模拟软件广泛借鉴。在广州、武汉、黄冈等地已开展的城市水系规划及排水规划中对EPA SW M M、Inf oW orks CS、DH I M IKE 进行了应用[3-4]，相对于 EPA SW M M这一开源软件，后期的商业模拟软件增加了数据预处理、结果分析、动态展示等功能。本文从模型的产汇流原理出发，选取EPA SW M M作为数学模型研究工具。

2 两种方法的理论基础

2.1 推理公式法

2.1.1 公式形式

目前广泛应用于城市雨水管渠设计流量的推理公式，英、美称为“合理化公式”，苏联称为“稳定情势公式”，由爱尔兰人摩尔凡尼于1851年提出[5]。原始形式见式（1）：

式中：Q为雨水设计流量，L/s；q为暴雨强度，L/（s·hm2）；ψ为径流系数；F为汇水面积，hm2。

推理公式法需结合暴雨强度公式使用，我国常用的暴雨强度公式形式见式（2）：

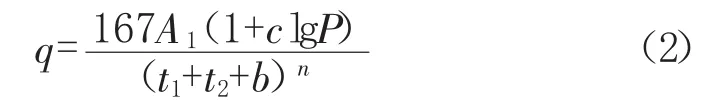
式中：A1、c、b、n 为地方参数，根据统计方法计算确定；t1为地面集水时间，m i n；t2为管内雨水流行时间，m i n；P为设计重现期，年。

2.1.2 公式基本假定

（1）降雨在整个汇水面积上的分布是均匀的。

（2）降雨强度在选定的降雨时段内均匀不变。

（3）汇水面积随集流时间增长的速度为常数。

2.2 数学模型法

该方法包括地表产流计算模型、地表汇流计算模型和管网汇流计算模型。

2.2.1 地表产流计算模型

将城市下垫面概化为三种不同分区，包括透水区域、有滞蓄量的不透水区域、无滞蓄量的不透水区域。对于有滞蓄量的不透水区域，产流量为降雨量减去洼地的填充量。对于透水区域，产流量为降雨量减去透水区域的滞蓄量和下渗量之和。对于透水区域的下渗计算，SW M M模型中有霍顿（H ort on）下渗模型、格林安普特（Green-Am pt）下渗模型和CN（Curve Num ber）模型可供选择。本文采用霍顿下渗模型，该模型假定下渗率在最初降雨时为最大值，随着降雨的持续，下渗率逐渐减小，最后达到稳定，此时的下渗率为稳定下渗率。城市雨水管渠集水区域面积较小，集水时间短，采用短历时设计暴雨，降雨过程中的蒸发量小，故产流计算时不考虑蒸发损失。

2.2.2 地表汇流计算模型

SW M M模型中，将子汇水区的三个不同分区近似概化为矩形的非线性水库，采用非线性水库法计算每个子汇水区出流量。

2.2.3 管网汇流计算

SW M M模型提供了两种求解非恒定流方法，包括运动波法、动力波法。运动波法假定水面坡度等于导管坡度，运用连续的动量方程求解，不能模拟回水、逆流、有压流的情况；动力波法是通过求解完整圣维南方程组来进行汇流演算。

2.3 输入与输出对比

相对于推理公式法，数学模型法在产汇流理论基础上进行细化，两者输入的参数和输出的结果不同。将输入参数分为确定性参数和经验性参数，确定性参数可根据现状资料得到，经验性参数需根据长期实测降雨流量资料率定后确定或参考同类地区确定。两种方法输入与输出对比见表1。

表1 两种方法输入与输出对比分析表

3 对比方案设计

3.1 变量选择

新版规范在建议采用数学模型法时是以汇水面积为主要指标，由表1可以看出，推理公式法和数学模型法在参数输入与结果输出时存在不同，综合考虑后确定以下设计变量：

（1）汇水面积。新版规范中提出，“当汇水面积超过2 km2时，宜考虑降雨在时空分布的不均匀性和管网汇流过程，采用数学模型法计算雨水设计流量”，已表明汇水面积是设计流量计算方法选择时的重要参考因素。因此将汇水区面积作为对比方案的自变量进行分析。

（2）汇水区形状系数。为汇水区平均宽度与汇水区长度之比，而汇水区平均宽度为汇水区面积与汇水区长度之比。汇水区形状系数可表示为f=F/L2（F为汇水区面积，L为汇水区长度）。扇形汇水区的形状系数较大，狭长形汇水区的形状系数则较小。中国各地区包括湖北、广东等省编制《暴雨径流查算图表》时，将汇水区形状系数作为汇流参数取值的依据。城市雨水管网一般呈树枝状形态，汇水区面积一定时，汇水区形状的不同将会影响支管峰值径流到达干管的时间，从而影响峰值径流遭遇过程，最终影响排水干管峰值流量。因此将汇水区形状系数作为对比方案的自变量进行分析。

（3）因变量。径流量峰值。

3.2 基本假定

3.2.1 汇水区模型

将汇水区概化为若干子汇水区，子汇水区均设为面积0.1 km2（400 m×250 m）的矩形区域，子汇水区的不透水率设为60%，子汇水区的平均坡度为0.5%。雨水干管（横向）长度设为400 m，雨水干管（纵向）长度设为250 m，雨水管坡度设为0.3%。为比较推理公式法和数学模型法在不同汇水区形状系数下的计算结果，子汇水区的排列概化为以下三种基本形式，如图1～图3所示。

图1 排列形式一

图2 排列形式二

图3 排列形式三

不同排列形式的汇水区形状系数f计算：

3.2.2 设计暴雨

采用武汉暴雨强度公式计算两年一遇设计暴雨总量，芝加哥过程线模拟暴雨过程，雨峰系数取为0.4。

3.2.3 管道平接方式

不同的管道平接方式会导致水力坡度不同，对径流峰值流量会有一定影响。管顶平接的水力坡度大于管底平接，按照一般性设计原则，采用管顶平接方式搭建管道模型。搭建管道数学模型时，雨水管径需要通过试算确定，以保证排水处于临近满流状态，而不出现溢流。雨水管道糙率取为0.013。

3.2.4 出流状态

采用自由出流设计，即下游排水口无顶托。

3.3 模型参数校准

由表1可以看出，数学模型法中需要确定的经验性参数较多，经验性参数需要长期的实测降雨及流量资料进行参数率定，而我国大部分城市已建排区尚未建立完善的排水防涝监测系统，新建排区在规划设计之初也无实测数据。模型参数若不进行校准，随意定量，模拟结果将不具备可靠性。因此在参考SW M M模型手册和同类文献[3-4]基础上，确定数学模型参数的初始值，再基于综合径流系数对数学模型中的经验性参数进行校准，以保证模型参数的可靠性。

4 结果分析

4.1 两种方法对汇水面积的响应分析

汇水区模型采用排列形式一（见图1），其中汇水区个数n为30，即总的汇水区面积为3.0 km2。采用SW M M数学模型法模拟排区的暴雨径流过程，即可得到不同汇水区面积（0.1～3.0 km2）的峰值流量。同时采用推理公式法计算不同汇水区面积的峰值流量，集水时间t1取10 m i n。两种方法对汇水面积的响应分析见表2。

表2 两种方法对汇水面积的响应分析对比

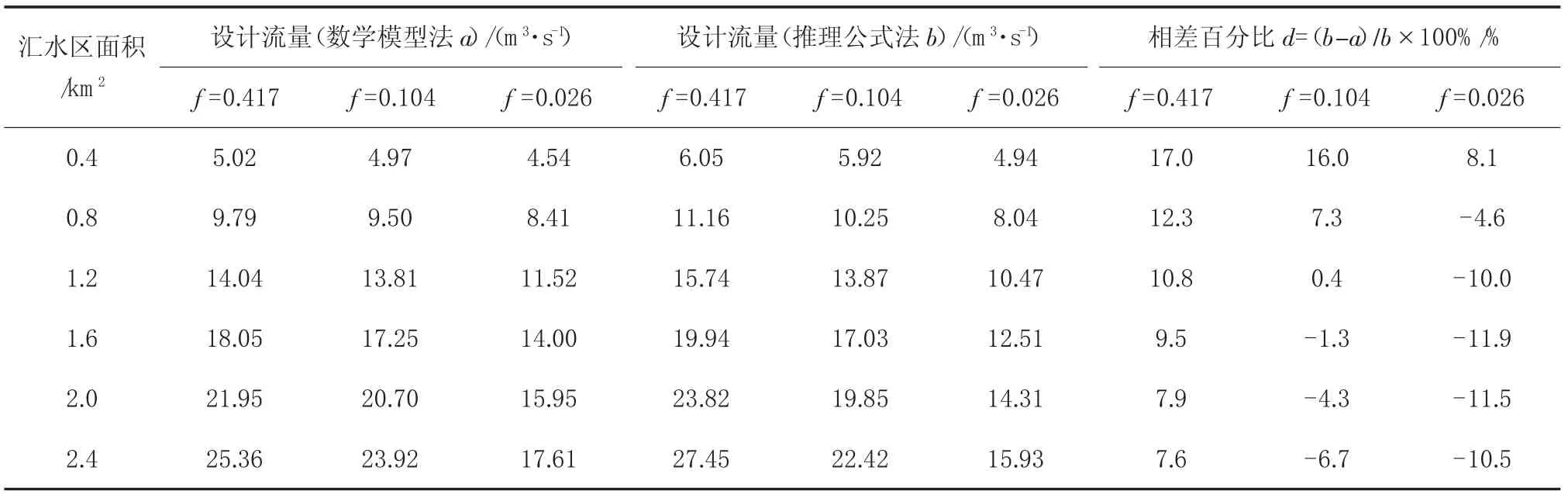
表3 两种方法对汇水区形状系数的响应分析对比

由表2可知：

（1）当汇水区面积小于0.6 km2时，数学模型法计算的设计流量小于推理公式法，随着汇水区面积的增大，相差百分比逐渐缩小；当汇水区面积为0.6 km2时，两者结果相当；当汇水区面积大于0.6 km2时，随着汇水区面积的增大，相差百分比先增大后缩小，且不大于12%。

（2）两种方法的设计管径随着设计流量增大而增大，且两种方法在同一汇水区面积时的设计管径相差不超过100 m m。

4.2 两种方法对汇水区形状系数的响应分析

汇水区模型分别采用图1～图3的三种排列形式，其中汇水区个数n为24，即总的汇水区面积为2.4 km2。经计算，三种排列形式的汇水区形状系数 f分别为 0.417、0.104、0.026。

采用SW M M数学模型法模拟汇水区的暴雨径流过程，即可得到同一面积下不同形状系数时的峰值流量。同时采用推理公式法计算同一面积下不同形状系数时的峰值流量，集水时间t1取10 m i n。两种方法对汇水区形状系数的响应分析见表3。

由表3可知：

（1）同一汇水面积时，设计流量与汇水区形状系数f相关，f值越大，即汇水区形状越偏于扁平，设计流量越大。

（2）不同汇水面积时，汇水区形状系数越大，推理公式法计算结果偏于安全；汇水区形状系数越小，数学模型法偏于安全。

5 结语

通过对汇水区下垫面和管网进行概化，研究了数学模型法和推理公式法的输入参数与输出结果的不同，在以综合径流系数校准数学模型基本参数的基础上，比较了两种方法在不同的汇水面积、汇水区形状系数等不同设计条件下的雨水流量计算结果，可以得出以下结论：

（1）对于汇水区面积小于3 km2或雨水管径小于d3 000 m m的雨水管网设计，两种方法计算结果相当，采用推理公式法简易且较为可靠；汇水区形状系数越大，推理公式法计算结果偏于安全。

（2）对于汇水区面积大于3 km2的城市排水干渠，汇水面积较大，汇流时间长，以短历时暴雨强度公式为基础的推理公式法不宜使用，往往采用1～3 d长历时设计暴雨，建议参考水利部门所采用的排涝计算方法[3-4]，根据汇水区内是否有存在较大蓄水容积、有无客水流经、自排或是抽排等情况，确定排水设施的适宜规模。