高强钢-混凝土组合梁极限承载力有限元分析

牛黎明

（甘肃公航旅陇漳高速公路管理有限公司，甘肃 定西748100）

0 引言

钢-混凝土组合结构是在钢结构和混凝土结构基础上发展起来的一种新型结构[1-8]。近年来，钢-混凝土组合梁在工程中已得到越来越广泛的应用。钢-混凝土组合梁用于城市立交桥和公路桥梁，可以节省高空支模工序和模板及脚手架，减少施工现场湿作业量，并且不中断下部交通。自1993年以来，仅北京市就已建成了以国贸桥为代表的80余座大跨钢-混凝土组合梁桥，在北京市道路建设及道路改造中发挥了重要作用。实践证明，钢-混凝土组合梁可以满足现代结构对“轻型大跨”、“预制装配”和“快速施工”的要求。

通常钢-混凝土组合梁肋部采用钢梁，顶板采用混凝土板，两者之间用剪力连接件连成整体。钢材和混凝土按组合梁桥的形式结合在一起，可以避免各自的缺点，充分发挥两种材料的优势，形成强度高，刚度大，延性好的结构形式。而高强钢-混凝土组合梁是在普通钢-混凝土组合梁的基础上，将钢材与混凝土强度提高，使二者的高强性能有机地结合起来而得到的新型钢-混凝土组合结构体系[3、4]。由于高强材料与普通材料力学性质的不同，高强钢-混凝土组合梁受力性能将不同于普通钢-混凝土组合梁，因此，对高强钢-混凝土组合梁受力性能进行研究是十分必要的。

1 单元类型及材料特性选择

由于钢与高强混凝土预应力组合梁的结构与受力比较复杂，在进行有限元分析时，应对其各个组成部分分别采用不同分析模型。现根据分析对象的具体情况，采用以下几种单元形式。

1.1 混凝土板

混凝土板采用8节点三维实体单元sol i d65，每个节点有3个平动自由度。该单元能够考虑材料非线性和几何非线性效应，能够较好地反映结构的实际受力状态。

采用多线性随动强化模型，首先输入混凝土的弹性模量和泊松比，然后再按照单轴的应力应变曲线，根据程序要求输入多个数据点，从而达到模拟材料的非线性本构曲线的目的。高强混凝土应力-应变本构关系为[4]：

式中：σc、εc分别为混凝土的应力和应变；σc0、εc0分别为混凝土的峰值应力与应变；fcu,10为混凝土轴心抗压强度。

1.2 钢梁

钢梁采用四节点非线性Shel l 143壳单元，采用双线性随动强化模型和Von M i ses屈服准则。首先输入钢梁的弹性模量和泊松比，然后输入屈服和切线模量。应力-应变关系为：

式中：E为钢材的弹性模量；Es为钢材的切向模量；εy为钢材的屈服应变；εu为钢材的极限应变。

1.3 连接单元

混凝土和钢梁上翼缘之间采用完全剪力连接，即在理想状态下，两者之间没有纵向滑移。通过耦合混凝土翼缘板和钢梁上翼之间的节点将两者连接在一起共同受力。

2 有限元分析

2.1 组合梁的基本参数

简支组合梁跨度L=5 000 m m，模型几何尺寸见图1所示。建立10根高强度材料比较模型（SCB1—10）和 2根普通材料比较模型（NSCB1、2），根据材料强度和几何参数的不同分成两组进行分析。编号Ⅰ（NSCB1、2及SCB1—6）保持模型几何尺寸不变，即混凝土翼板厚为100 m m，混凝土翼板宽为600 m m不变，逐渐改变混凝土和钢梁强度，具体参数见表1所列；编号Ⅱ（SCB3及SCB7—10）混凝土强度均为C70、钢梁采用Q390不变，只改变组合梁几何参数，其中SCB7、8混凝土翼板厚度分别取90 m m和110 m m，SCB9、10混凝土翼板宽度分别取400 m m和800 m m。混凝土材料性质见表2所列。

2.2 有限元模型的建立

采用从低级图元到高级图元的的方法：即先通过关键点分别定义钢梁的翼缘和腹板并粘结为一体；再用同样的方法定义混凝土翼缘板。在钢梁与混凝土翼缘板交界面处，由于不考虑混凝土翼缘板和钢梁之间的滑移效应，所以通过耦合连接在一起，共同受力。

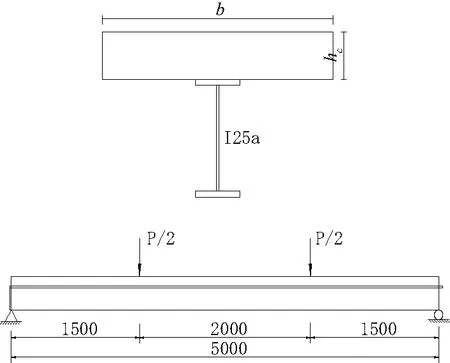
图1 模型梁示意图

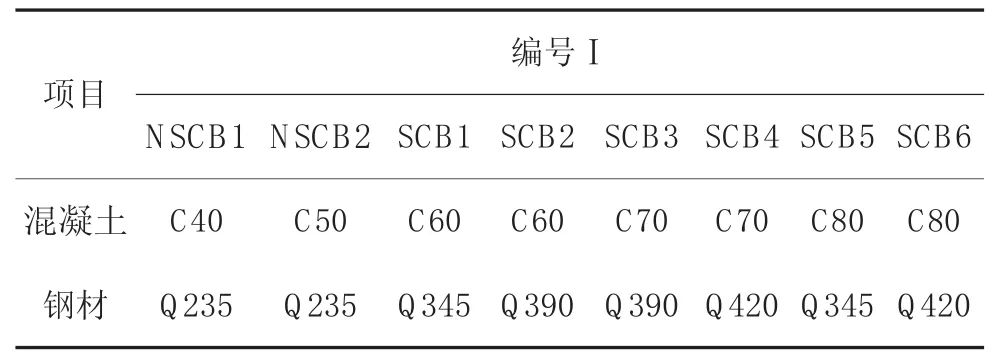
表1 材料及主要参数一览表

单元网格的大小、形状直接影响分析的准确性和效率，是有限元分析的重要环节。该模型中采用映射网格划分，单元尺寸为50 m m，这样划分的单元收敛性能较好，划分后的有限元模型见图2所示。采用跨中两点对称施加集中荷载。为防止应力集中造成收敛困难，在加载处及支座处分别设置刚性垫板。

3 计算结果分析

3.1 应力与应变分析

通过计算，可以得到组合梁在不同荷载下的应力与应变。当荷载达到极限荷载的50%左右时，钢梁下翼缘开始屈服，此时，钢梁上翼缘和腹板及混凝土翼板应变都很小，组合梁仍处于弹性工作状态；随着荷载的增加，钢梁腹板逐渐屈服，中和轴上移，受压混凝土应变增加，钢梁腹板屈服范围越来越大，在极限状态时，跨中钢梁腹板大面积屈服，跨中混凝土翼缘板顶部应变达到0.003 3，混凝土压碎，试件破坏。

表2 混凝土材料性质一览表

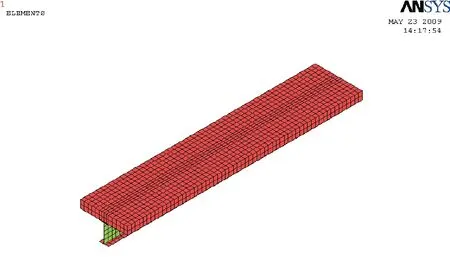
图2 组合梁有限元模型

3.2 跨中挠度

3.2.1 材料强度对组合梁跨中挠度的影响

表3为NSCB1、2与SCB1～6各模型梁的屈服荷载、极限荷载及相应挠度值。由表3可知，钢梁下翼缘的屈服荷载为极限荷载的50%左右，即当荷载小于等于极限荷载的50%时，组合梁处于弹性工作阶段。图3为SCB1～6与NSCB1、2模型梁荷载-跨中挠度曲线。与普通组合梁的荷载挠度曲线类似，可以分为三个阶段。

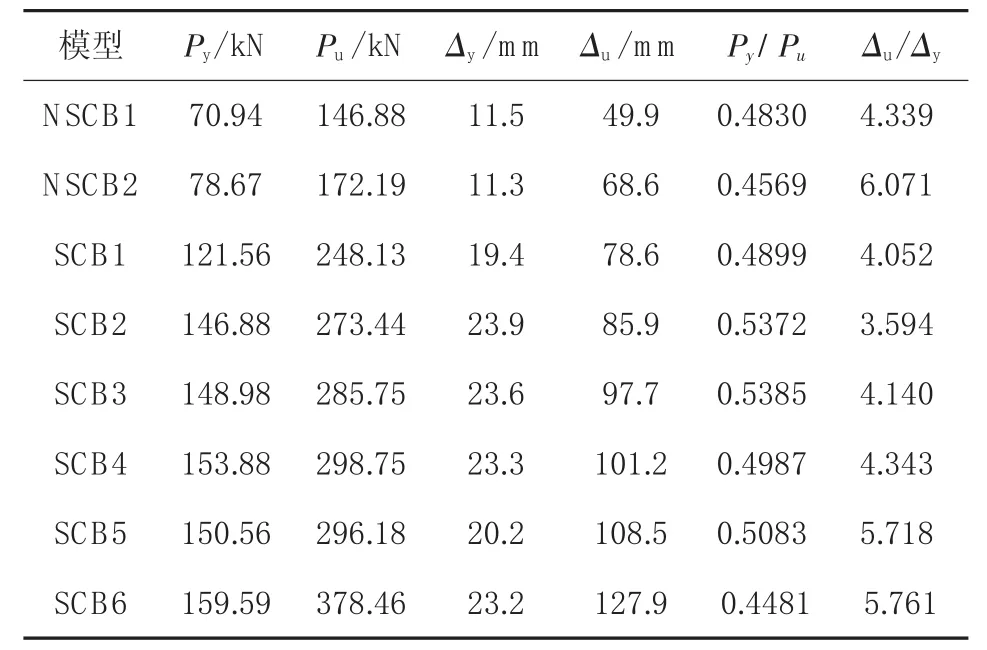
表 3 NSCB1、2与SCB1～6的屈服荷载、极限荷载及相应挠度值一览表

图 3-1 SCB1～6、NSCB1～2 荷载 -跨中挠度曲线图（1）

图 3-2 SCB1～6、NSCB1～2 荷载 -跨中挠度曲线图（2）

（1）弹性工作阶段（P/Pu≤0.5）。从加载到钢梁下翼缘开始屈服，屈服荷载定义为Py，将Py视为组合梁弹性阶段终点的标志。由图3可见，从加载到Py时，高强钢-混凝土组合梁SCB1～6的荷载与跨中挠度近似呈线性关系，普通钢-混凝土组合梁NSCB1、2也为线性关系，各模型跨中挠度在11.3～23.9 m m之间，并且由表4可以看出，挠度的变化与材料强度的变化之间无明显的数值关系。当模型的几何参数相同时，材料强度对弹性阶段跨中挠度影响趋势不明显。这说明混凝土强度和钢梁强度对组合梁在弹性工作阶段的刚度及弹性工作范围影响较小。

（2）弹塑性工作阶段（0.5＜P/Pu≤1.0)。钢梁屈服后，即P＞Py后，由图3可以看出，随着荷载的增加，组合梁截面刚度逐渐降低，挠度发展速率高于荷载发展速率，截面内力发生重分布，荷载与挠度呈现出明显的非线性关系。在荷载达到Pu时，各模型的跨中挠度在49.9～117.9 m m之间，NSCB1的挠度为49.9 m m，SCB6的挠度为127.9 m m，挠度增大了156.3%，相差明显，说明材料强度对弹塑性阶段的挠度影响显著。结合表3及图3比较SCB1和SCB5、SCB5和SCB6可以看出，当钢梁强度不变，混凝土强度从C60提高到C80时，极限挠度增大了38%；当混凝土强度不变，钢梁强度从Q345提高到Q420时，极限挠度只增大了17.9%。可见，混凝土强度提高对极限挠度所产生的影响比钢材强度提高产生的影响显著。

（3）下降段。当P达到Pu时，由于受压区混凝土的脆性破坏导致组合梁承载力迅速下降，图3中未给出下降段，是由于这一阶段破坏迅速，有限元程序无法在短时间内得到计算结果，这也说明了高强钢-混凝土组合梁在达到极限状态后脆性破坏显著的特点。

3.2.2 几何参数对组合梁跨中挠度的影响

表4为NSCB1、2与SCB1～6各模型梁的屈服荷载、极限荷载及相应挠度值。图4为SCB3与SCB7～10模型梁荷载-跨中挠度曲线。由表4可以看出，在弹性工作阶段，各模型跨中挠度在19.4～23.8 m m之间，减小混凝土翼板厚度或宽度屈服挠度增大，增大混凝土翼板厚度或宽度屈服挠度减小，但影响程度较小，可见几何参数的变化对组合梁弹性阶段的跨中挠度影响不显著。

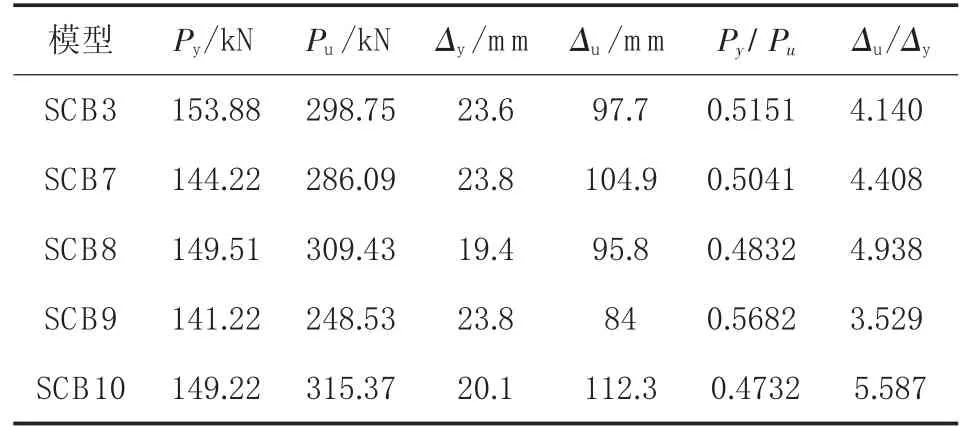
表 4 SCB3与SCB1～6的屈服荷载、极限荷载及相应挠度值一览表

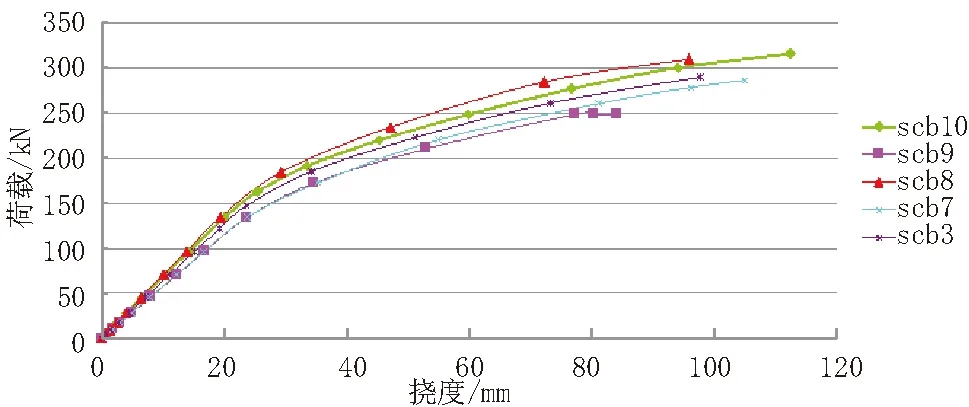
图4-1 SCB3、7～10荷载-跨中挠度曲线图（1）

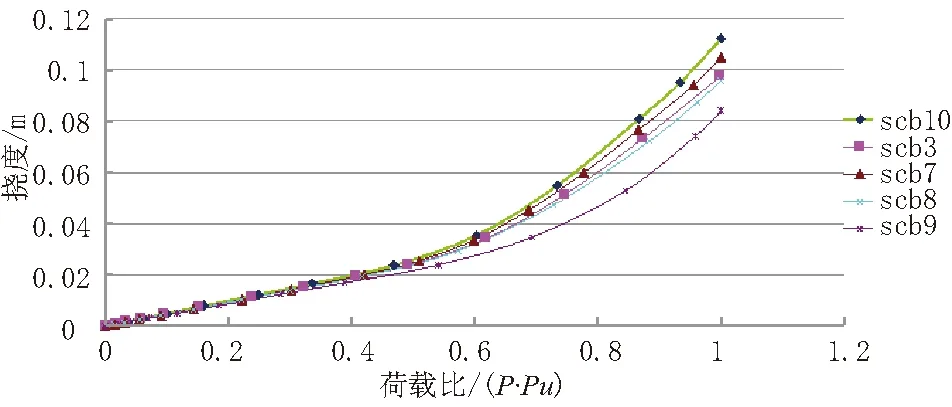
图4-2 SCB3、7～10荷载-跨中挠度曲线图（2）

在进入弹塑性工作阶段以后，由表4可以看出，混凝土翼板厚度对极限挠度的影响趋势与弹性阶段相同，且程度较小；混凝土翼板宽度对极限挠度的影响与弹性阶段有所不同，极限挠度随混凝土翼板宽度的增大而增大，减小而减小。影响程度也较混凝土翼板厚度大。从图4可以看出，在极限状态时，由于几何参数的不同，荷载挠度曲线有较明显的变化，SCB9、10的荷载挠度曲线偏离SCB3的程度比SCB7、8大，说明混凝土翼板宽度的影响大于混凝土翼板厚度的影响，增加混凝土翼板宽度可以提高梁的延性。

3.3 承载力分析

由表3可知，随着材料强度的提高，组合梁的极限承载力逐渐提高，比较SCB1和SCB5、SCB5和SCB6可以看出，当钢梁强度不变，混凝土强度从C60提高到C80时，极限承载力提高了18%；当混凝土强度不变，钢梁强度从Q345提高到Q420时，极限承载力提高了28%；可见钢梁的影响大于混凝土的影响；比较SCB1和SCB6，即同时提高混凝土强度和钢梁强度，极限承载力提高了53%。由表4可知，几何参数的变化对组合梁极限承载力有一定的影响，但影响程度不明显，且混凝土翼板宽度比混凝土翼板厚度的影响显著。

4 结语

（1）随着翼缘板混凝土强度的提高，组合梁跨中受压区混凝土破碎的现象趋于明显、剧烈，但是，高强钢-混凝土组合梁仍具有很好的延性。随着混凝土强度等级或者混凝土翼缘板宽的增加，组合梁极限挠度及延性都会有较大的提高。

（2）通过对混凝土强度、钢材强度，以及混凝土翼板厚度、宽度不同的组合梁的比较，发现钢梁屈服前即弹性工作阶段，不同材料组合、不同几何参数对跨中挠度的影响不明显；在进入屈服状态以后，高强钢-混凝土组合梁参数的变化会对其力学性能产生较大的影响，混凝土强度和混凝土翼板宽度对跨中挠度有较大影响，钢梁强度和混凝土翼板厚度对跨中挠度的影响不显著。

（3）提高钢梁强度是提高组合梁极限承载力的有效途径，混凝土翼板宽度对组合梁极限承载力的贡献比混凝土翼板厚度显著。简单地提高混凝土的强度等级对于组合梁承载力的提高效果不大，要提高高强钢-混凝土组合梁的承载力，需要对其它参数进行优化组合，包括提高钢梁的强度和混凝土板宽度等。