基于MRAI的伺服系统转动惯量辨识及改进研究
董海军,段剑文
(1.杭州桢正机器人科技有限公司,浙江 杭州 311121;2.杭州职业技术学院 友嘉机电学院,浙江 杭州 310018)
0 引 言
随着自动化水平的提高,伺服系统的使用越来越广,而控制参数的自整定非常有必要。为实现控制参数整定,通常需要知道整个机械系统的系统转动惯量[1]。虽然可以通过机械部件的转动惯量折算来得到近似值,但是,当机械系统比较复杂时,转动惯量折算也容易出错,而且不一定准确。因此,转动惯量的辨识是实现控制参数自整定的首要问题。惯量辨识精度将影响使用整定控制参数时伺服系统响应是否能达到期望效果。
根据辨识原理不同,转动惯量辨识主要有以下几种方法:(1)加减速法[2-3];(2)最小二乘法[4-5];(3)模型参考自适应法等[6-9]。其中,加减速法的原理最为简单,实现方便;最小二乘法和模型参考自适应法的原理较复杂、计算量较大,但可实现实时辨识。
本文将对基于模型参考自适应的转动惯量辨识方法进行推导分析,并针对方法中的关键参数即辨识增益提出一种自适应调整方法,以解决辨识响应快速性和稳定性的矛盾。
1 基于MRAI的转动惯量辨识及改进
1.1 模型参考自适应辨识算法
模型参考自适应辨识(MRAI)是由模型参考自适应控制的思想衍化而来的,其典型的MRAI的原理框图如图1所示。

图1 MRAI的原理框图
设伺服电机的机械运动方程为:
(1)
式中:Te—电磁转矩;TL—负载转矩;J—系统转动惯量;ω—机械角速度;t—时间。
基于POPOV稳定性定理的惯量辨识算法如下:
(2)
以上3式分别作为参考模型、可调模型和自适应辨识律,自适应辨识律设计为比例积分型算法。
以上为连续模型,当在计算机或微控制器上实施模型参考自适应参数辨识时,需要导出离散时间域的自适应控制规律。离散化过程中会导致自适应控制回路中出现一个固定延时。因此,有必要对离散时间的模型参考系统直接建立一套控制算法。
由于MRAI算法是基于稳定性理论设计的,在保证被辨识参数渐进收敛的同时,并不需要考虑系统的稳定性,这就为研究带来了很大方便。
将式(1)离散化可得:
(3)
式中:T—采样周期。
将相邻计算周期的运动方程相减可得:

(4)
在快速响应的伺服系统中,采样频率很高,在一个采样周期内,可以认为负载转矩不变,则:
ω(k)=2ω(k-1)-ω(k-2)+bΔTe(k-1)
(5)
其中:ΔTe(k-1)=Te(k-1)-Te(k-2),b=T/J。
将上式作为参考模型,可得可调模型方程为:
(6)
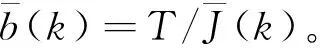
根据Landau离散时间递推参数的辨识机制,构建自适应辨识律为:
(7)
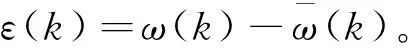
式中:β—辨识增益。
1.2 辨识增益β的自适应调整
基于MRAI的转动惯量辨识方法中,辨识增益β为重要参数,辨识增益β的大小直接影响转动惯量发生变化时的惯量辨识速度和转动惯量维持稳定时的惯量辨识波动。辨识增益越大,转动惯量发生变化时惯量辨识速度越快,但是转动惯量维持稳定时惯量辨识波动越大;辨识增益越小,转动惯量发生变化时惯量辨识速度越慢,但是转动惯量维持稳定时惯量辨识波动越小。本研究为解决这个矛盾,建立辨识增益和当前辨识结果之间的关系,通过对当前辨识结果的分析,选择更合理的辨识增益,实现辨识增益的自适应调整,改进原辨识方法。
设当前为第k个辨识周期,则最新的n+1个惯量辨识结果分别为:
Jest(k),Jest(k-1),……,Jest(k-n)。
基于上述辨识值,建立以下惯量辨识结果评价标准:
(8)
即为n个当前辨识结果和前一时刻辨识结果差值的绝对值之和与电机惯量的比值。基于辨识结果评价标准,建立辨识增益β的分段函数:
(9)
式中:β0—预设基准辨识增益;h—比例缩放因子。
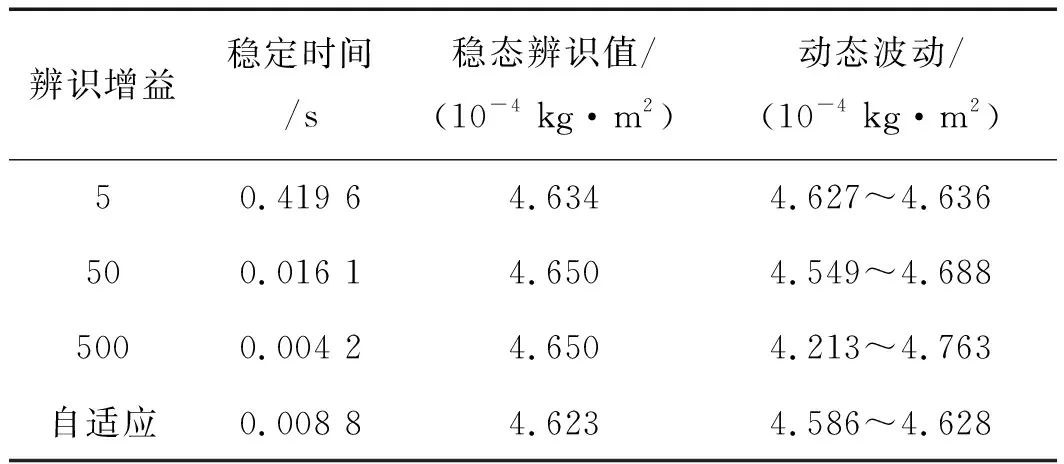
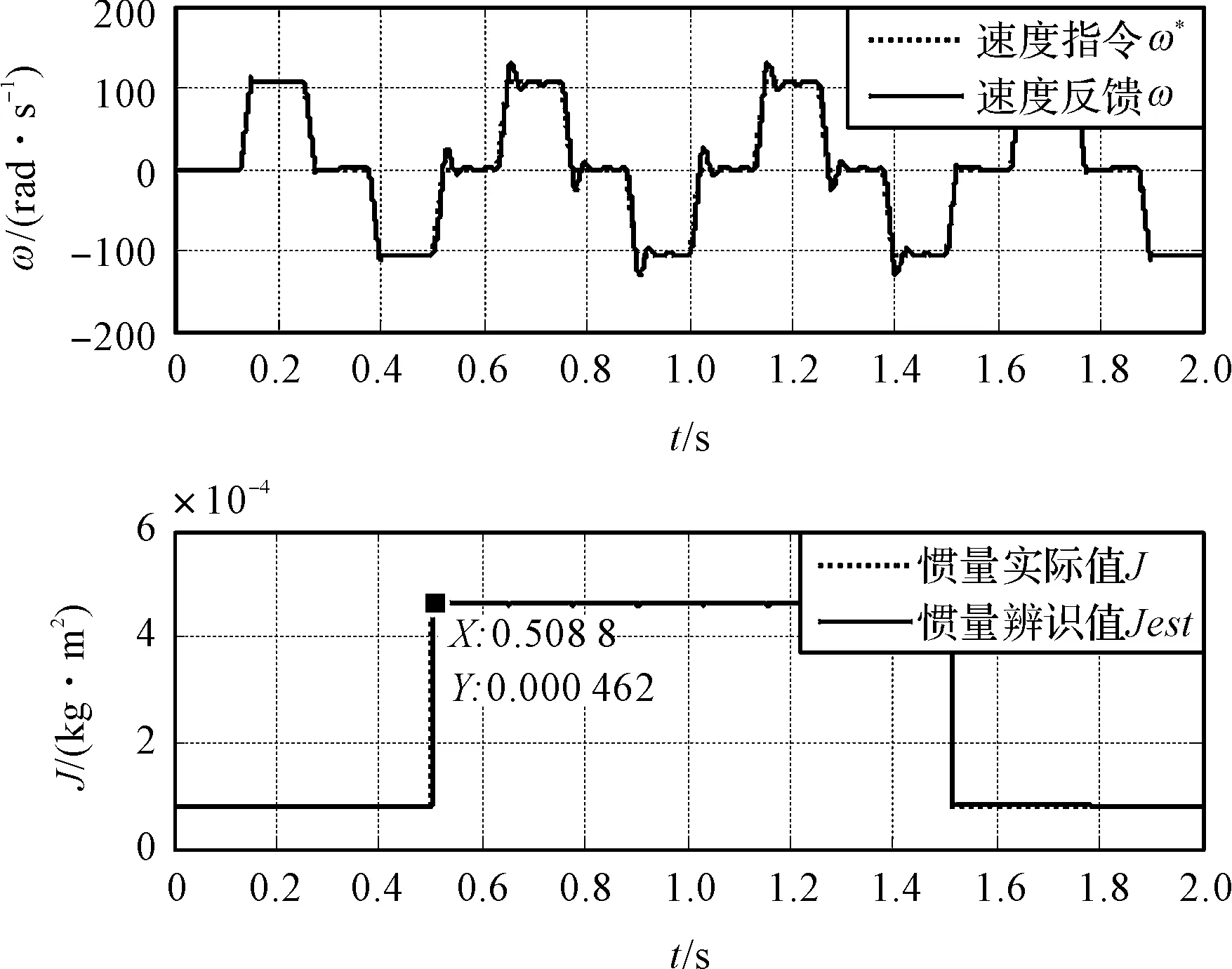
当S≥b,即辨识结果还不稳定时,令辨识增益比例放大为基准辨识增益的h倍;当S≤a,即辨识结果稳定时,令辨识增益比例缩小为基准辨识增益的1/h倍;当a 辨识算法框图如图2所示。 图2 辨识增益β自适应调整的MRAI辨识算法框图 基于上述辨识增益β的自适应调整方法,当实际转动惯量变化较大时,惯量辨识值可以快速跟随这种变化;当实际转动惯量维持稳定,系统控制指令变化时,惯量辨识波动较小。 对于上述转动惯量辨识算法,本研究使用Matlab建立了Simulink模型进行仿真实验分析。 其中,对于永磁同步电动机的数学模型,假设定子磁场为正弦分布,不考虑谐波与饱和,在d-q坐标系下PMSM的电压方程和电磁转矩方程如下: (10) Tem=pn[ψfiq+(Ld-Lq)idiq] (11) 式中:ud,uq,id,iq—d轴、q轴的定子电压和定子电流;Ld,Lq—d轴、q轴定子电感;Rs—定子绕组电阻;ωe—转子电角速度;ψf—永磁体磁链;pn—极对数。 仿真模型中使用的伺服电机采用矢量控制技术,转动惯量辨识模块按照前述的模型参考自适应辨识方法进行搭建。电机参数如表1所示。 表1 电机参数 实验分析时,首先设置辨识增益β=50,基于上述惯量辨识算法得到不同负载惯量时的惯量辨识结果,验证了基于MRAI的转动惯量辨识方法的可行性;然后,分析了采用不同辨识增益时对惯量辨识响应的影响;最后,采用辨识增益β自适应调整的惯量辨识方法进行实验,并将辨识响应结果与前述固定辨识增益的辨识方法进行了对比。 为测试惯量辨识算法精确性,本研究令负载转动惯量分别为2~10倍电机惯量,辨识结果如表2所示。 表2 转动惯量辨识值及其误差分析 由表中数据可知:当负载转动惯量在2~10倍JM之间变化时,转动惯量辨识的稳态误差在10%以内。可见辨识精度高,可为控制参数自整定提供依据。 使用模型参考自适应的方法来进行转动惯量辨识时,自适应辨识增益β的大小将影响辨识算法对系统转动惯量变化的响应速度。 为分析辨识增益对辨识结果的影响,本研究令负载转动惯量按下述方式变化:当t=0时,负载转动惯量JL=0,则系统惯量Jt=JM+JL=0.000 077 kg·m2;当t=0.5 s时,负载转动惯量JL=5*JM,则系统惯量Jt=6*JM=0.000 462 kg·m2;当t=1.5 s时,负载转动惯量JL=0,则系统惯量Jt=0.000 077 kg·m2。 本研究分别设置自适应增益β为5、50和500进行惯量辨识,得到的电机速度和转动惯量辨识值波形如图(3~5)所示。 图3 β=5时的电机速度和转动惯量辨识值波形 图4 β=50时的电机速度和转动惯量辨识值波形 图5 β=500时的电机速度和转动惯量辨识值波形 测量图(3~5)中的惯量辨识稳定时间(即从负载惯量变化到惯量辨识值稳定的时间)、稳态辨识值和动态辨识误差,得到的数据如表3所示。 表3 不同辨识增益β时的辨识性能 辨识增益β=5时,辨识结果稳定所需时间最长,但是稳态时的惯量辨识值动态波动最小。辨识增益β=500时,辨识结果稳定所需时间最短,但是稳态时的惯量辨识值动态波动最大。辨识增益β=50时,则得到了一个折中的性能,但还不够好。 基于上述实验测试波形和数据,验证了辨识增益β对惯量辨识静动态响应的影响:即辨识增益越大,则惯量辨识收敛速度越快,但动态波动较大;辨识增益越小,则惯量辨识收敛速度越慢,但动态波动较小;辨识增益对稳态辨识值影响有限。 相同实验条件下,本研究采用上文所述的辨识增益β自适应调整的惯量辨识方法,并取基准辨识增益为50进行测试,其中,电机速度和转动惯量辨识值波形如图6所示。 图6 β自适应时的电机速度和转动惯量辨识值波形 通过惯量波形和表3中性能数据的对比可知:当辨识增益β采用自适应调整规则时,辨识性能得到提升,惯量辨识值能快速又精确地跟随负载转动惯量的变化,验证了所提出辨识算法的优越性。 为分析本文所提出方法在实际工程中的效果,笔者在实际伺服系统中进行测试。实际系统惯量为0.78*10-4kg·m2。采用辨识增益固定和辨识增益自适应调整的惯量辨识方法分别测试,得到以下结果:辨识增益β=2固定时的转动惯量辨识值波形如图7所示。 图7 β=2时的转动惯量辨识值波形 辨识增益β自适应时(β0=2)的转动惯量辨识值波形如图8所示。 图8 β自适应时(β0=2)的转动惯量辨识值波形 两者对比可知: (1)稳态响应。稳态波动上两者相差不大,辨识增益β自适应时的波动幅度稍小一点。稳态误差基本上在11%以内; (2)暂态响应。辨识增益β自适应时,经过0.8 s左右,惯量辨识结果达到惯量实际值,并趋于稳定,其稳定时间明显小于辨识增益β=2时的1.5 s。 本文提出了一种基于辨识增益β自适应调整的改进算法,并对此辨识算法搭建了仿真模型,进行了仿真测试和实际系统测试,得到了不同辨识增益时的转动惯量辨识值波形和性能数据。 实验结果显示:惯量辨识精度基本上在11%以内,可以满足伺服控制参数自整定的需求;而且在辨识值稳态波动变化不大的情况下,采用辨识增益β自适应调整的惯量辨识方法,辨识稳定时间可以减小将近46%。 由此可见,本文所提出的辨识改进算法可以明显改善惯量辨识响应,具有良好的动态和稳态性能,能够跟踪系统转动惯量的变化。
2 仿真分析
2.1 仿真模型建立

2.2 不同负载惯量时的辨识误差分析

2.3 不同辨识增益对辨识性能的影响

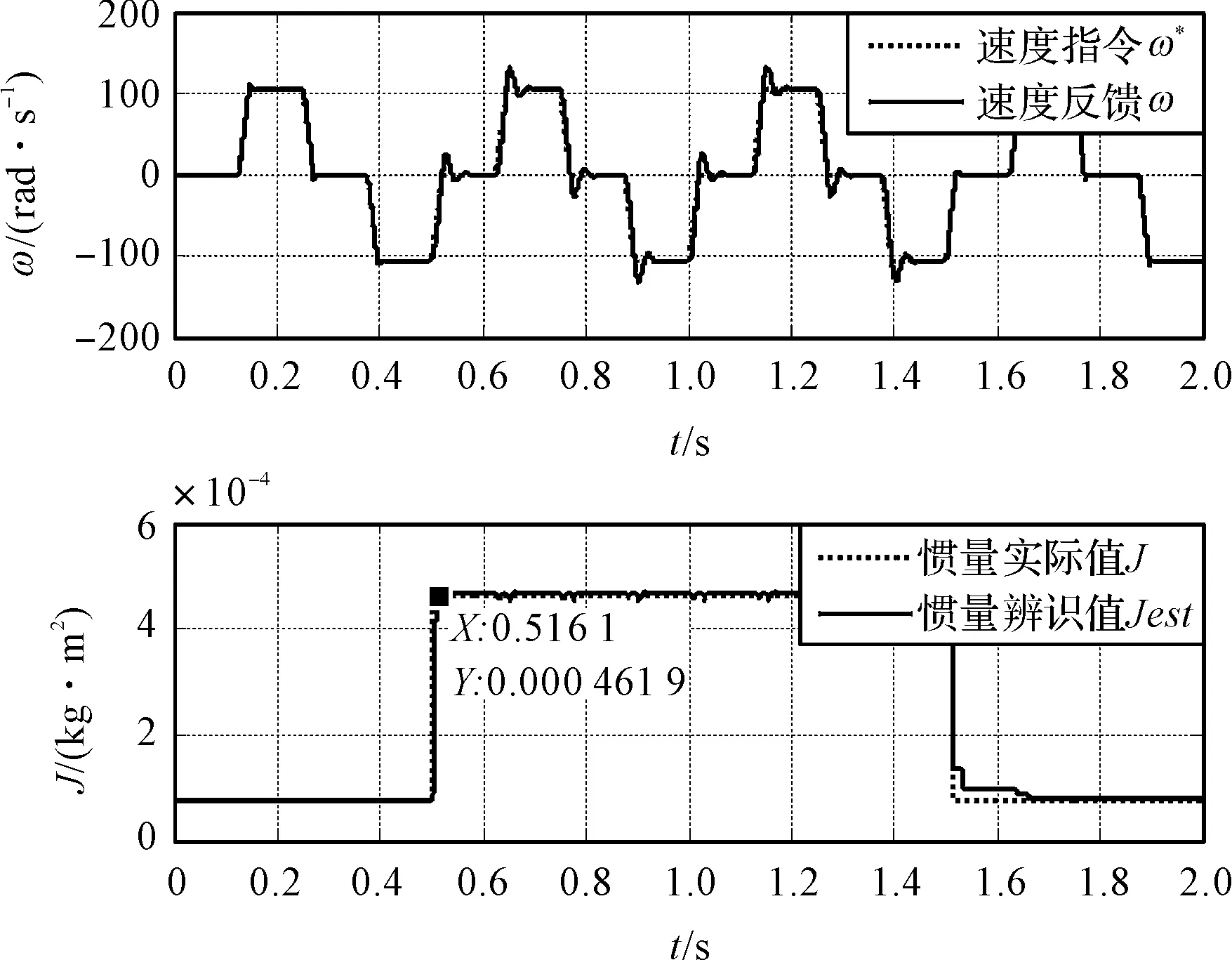
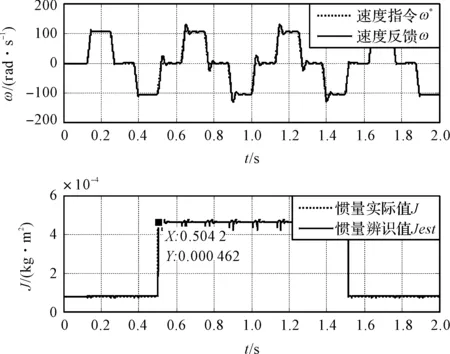
2.4 辨识增益自适应调整时的结果
3 测试验证


4 结束语

