再制造成本效益的一种定量分析模型及应用*

李 飞，江志刚，王艳红

(武汉科技大学 a.机械传动与制造工程湖北省重点实验室；b.冶金装备及其控制教育部重点实验室；c.恒大管理学院，武汉 430081)

0 引言

再制造是废旧资源再利用、发展循环经济并创造经济增长点的重要途径[1]。再制造产品的质量与性能达到或超过新品，使得废旧产品通过再利用实现价值的增值[2]。产品增值与否与产品再制造的成本和效益密切相关。不同产品或零部件服役工况不同从而导致不同的失效形式，其再制造所需成本及所获效益也不尽相同。因此，再制造企业对退役产品以何种方式进行处理，是否能通过再制造获得价值的增值，需要对其进行再制造成本效益分析。

目前，针对再制造成本效益分析方面的研究，文献[3]从废旧零部件失效形式的角度，对废旧零部件再制造的工艺过程经济性进行评估，分析不同失效形式再制造对经济效益的影响。文献[4]以再制造产品的回收策略为基础建立了层次拆卸模型，从成本分析的角度提出报废汽车拆卸的总收益数字模型，为再制造拆卸回收经济性提供有效支持。文献[5]从装备复杂结构角度，建立不同层次(整机、总成和零件)的再制造成本构成模型，为再制造经济性分析提供理论指导。文献[6]从材料(废旧产品)采购成本的角度，分析出材料成本不确定性越大，对再制造系统经济性决策影响越大。文献[7]从再制造工艺的角度，建立再制造加工过程的成本定量评价模型，并评价基于增材制造技术上的再制造经济效益。文献[8]从零部件重用角度，考虑再制造加工操作关键因素成本并建立经济效益决策模型，优化某产品族下不同成本效益。以上文献从装备结构、产品拆卸回收以及加工等再制造过程的不同环节进行成本和效益分析，对于产品再制造性评估具有一定的指导意义。然而，从再制造企业实际需求出发，再制造成本效益的精确分析需从整体的角度考虑再制造的产品回收、产品加工以及产品销售这一总体流程。此外，产品再制造环节较多，工艺复杂，对再制造成本和效益造成影响的因素交错繁多，为提高分析的有效性，应该从集成的角度分析各因素对再制造成本效益综合影响。

基于此，考虑再制造整体流程，提出一种再制造成本效益定量分析模型，为再制造造企业进行产品再制造的效益决策提供支持。

1 再制造成本效益分析的影响因素体系

产品再制造是一项复杂的系统工程，其多环节多工序的特点导致再制造成本效益的影响因素繁多，给再制造成本效益的分析增加了难度。为有效分析再制造各环节中各个因素对再制造成本效益的综合影响，提高再制造成本效益分析的准确性，建立了包括废旧产品的采购、加工以及产品销售的再制造工艺流程，如图1所示。

图1 再制造工艺流程

根据再制造工艺流程，从采购、加工和销售三个方面对再制造成本效益的影响进行分析。

废旧产品作为再制造的原材料(毛坯)，需要再制造商从外界采购获取，而影响再制造成本效益的采购因素主要体现在：①采购数量(NOP)；②采购价格(COP)；③采购质量(QOP)；④运输成本(TC)。

废旧产品拆卸后经过技术检测，对于可再制造零部件，将采用一系列的加工工艺对其进行恢复。此时，影响再制造成本效益的因素可分为加工因素和材料利用因素。加工因素即企业再制造设施的建设及管理，包括以下方面：①工艺能力(PC)；②运营成本(OC)；③库存成本(IC)；④工艺柔性(FP)。加工过程中，材料并不是百分百利用，有废旧材料的丢弃，也有新材料的购买，因此材料利用也是再制造成本效益的重要影响因素，所需考虑的经济性因素有以下几点：①零部件利用率(RPU)；②废料丢弃成本(CUD)；③新零部件购买成本(CNP)。

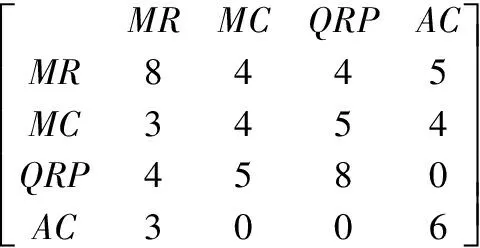
再制造产品需面向市场销售才能获得经济效益，同时再制造商需通过系列营销推广让消费者接受认可。该过程所需考虑的经济性因素如下：①市场需求(MR)；②市场竞争(MC)；③再制造产品质量(QRP)；④广告费用(AC)。

综上，建立再制造成本效益因素的指标体系如图2所示的。

图2 再制造成本效益的影响因素体系

2 再制造成本效益定量分析模型

再制造成本效益的各个影响因素相互作用、相互影响，且每个因素都包含多个子因素，因此难以有效定量计算每个因素对成本效益的影响。图论是一种采用点与线表示事物之间联系的数学方法，其中有向图能定性表示各因素及其各个子因素的相互作用和影响，而有向图的连接矩阵可定量分析各个因素的相互作用程度[9]。基于此,采用图论方法对再制造成本效益的影响因素进行分析，计算各个因素对再制造成本效益的综合影响程度，并用再制造成本效益指数来表示产品再制造的经济性。

2.1 基于图论的再制造成本效益影响因素分析

图论研究的对象是图，通常用点代表影响因素，用两点间的连线表示影响因素间的作用关系。本文选择有向图作为图论代表中的常用模型，其具有以下特征：

(1) 有向图包含许多节点，且有向边连接不同节点。节点的数量等于影响因素的数量。如果因素“i”对因素“j”有影响作用，那么有向边的箭头将从“i”指向“j”，反之亦然。这样可表示出不同因素之间的内部联系。随着节点数增加，图形变复杂，有必要将其转化成矩阵。

(2) 根据有向图得出连接矩阵。该矩阵中，对角线元素Aii表示第i个因素对整个系统的影响程度。非对角线元素Aij，表示因素“i”对因素“j”的影响。换言之，该矩阵表明了各个要素的相互依存性。

根据图论性质，将图论方法的研究应用于再制造工艺过程成本效益分析，对影响再制造成本效益的4个主要因素，即采购因素(PR)、加工因素(PS)、材料利用因素(MU)和市场因素(MA)进行定性分析。这4个因素对应有向图的4个节点，各个因素的相互相互作用关系如图3所示。

图3 再制造成本效益影响因素有向图

图3中的采购因素可影响加工因素、材料利用和市场因素，因为采购的废旧产品将用于加工过程，废旧产品质量的优劣程度将影响加工恢复质量，材料的利用以及后期再制造产品的销售。然而，产品再制造过程从采购到加工，再销售到市场这一过程不可逆，因此后者不能影响前者。同理可知，加工因素和材料利用因素、采购因素和市场因素都是相互影响。

根据有向图可得出其连接矩阵为：

在矩阵中对角线元素Aii表示该影响因素对整个系统成本效益的影响强度。非对角线元素Aij表示因素i对因素j的作用值大小。如果没有箭头从特定的节点‘i’指向节点‘j’，那么矩阵中Aij相应的值应为0, 因此矩阵中A21、A31、A43取值为0，其他值有待确定。

同理，可分别做出各子因素的有向图和连接矩阵。

2.2 再制造成本效益定量分析模型建立

再制造成本效益的各影响因素相互作用相互影响，具有相互依存性，且每个因素的涵义和重要程度(权数)不同，对成本效益的影响趋势(积极或消极)和影响幅度(增加或减少)也不同。利用有向图矩阵定量分析各个影响因素对再制造成本和效益的正负影响，计算各因素对再制造成本和效益的综合评价值。

同时，采用再制造成本效益指数对再制造成本效益定量分析，反映各个因素影响的综合变动情况。指数值越大，各个因素对再制造成本和效益的积极影响越大，则该产品能最小化再制造成本，为企业最大化经济效益；指数值越小，则各个因素对再制造成本和效益的消极影响越大，该产品再制造为企业带来的利润相对较小甚至可能亏损。

建立再制造成本效益指数定量分析模型的具体计算步骤如下：

(1) 采用德尔菲专家评判法确定各影响因素间的相互作用值。按照“德尔菲法”确定的程序和要求，向若干个专家进行问卷调查，确定各个因素间的相互作用强度，即Aij的取值可为{(1, 2, 3, 4, 5)=(很弱，弱，中等，强，很强)}。

专家评判较为主观，难以有效确定最佳方案。在此基础上，引进专家意见值可靠性指数，考虑各因素的一致性和协调性，构建专家意见集成搜索模型，使评分结果最优[10]。专家意见集成的优化搜索模型如下：

(1)

(2)

其中，ai为第i个专家给出的评价值，xi为第i个专家在原来基础上经优化搜索后得到的评价值，pi为第i个专家的权重，ζ(xi)为第i个专家的意见可靠度，Ψ(x)为群众意见可信度，Ψ0为最初设定的可靠性标准，Ek为集成函数的峰度，σ(x)为根方差，U(x)为加权均值，ri为评价值的最大允许调整量。

当可信度大于或等于85%时，认为非常可信；可信度为70%～84%，为满意水平；55%～69%为可接受水平；小于55%，说明一致性和协调性方面存在问题，专家意见的分歧较大，必须进行聚类分析，然后对不同类别分别集成，集成后进行选择，获得唯一结论。

(2) 采用熵权法确定各因素对再制造系统成本效益的影响，即Aii的取值。具体步骤[11-12]如下：

①确定各因素对系统作用强度评分，即Aii的取值可为{(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)=(非常弱，很弱，较弱，微弱，中等，微强，较强，强，很强，非常强)}。

②计算专家评分的标准化矩阵。设有m个影响因素、n个评分专家，其矩阵为A=(aij)m×n，对其进行标准化处理，得到R=(rij)m×n，则：

(3)

③求各专家评分的信息熵。其中，第i个指标的熵值为：

(4)

④确定专家评分的权重。第i个指标的熵权为：

(5)

⑤对各个影响因素进行评分。根据计算出的专家评分权重对各个指标进行评分，设gi为第i项指标的最终得分，则：

(6)

(3)利用矩阵计算各因素综合影响值。通过德尔菲法和熵权法可确定各影响因素之间的相互作用值(非对角线元素的取值)及各因素对再制造系统成本效益的影响值(对角线元素的取值)。然后可求得各影响因素的综合影响值，可以表示为：

(7)

其中，i、j表示影响因素，aij表示元素i对元素j的影响程度，ai、aj表示影响因素最终得分，wi、wj表示影响因素的权重。

根据上述模型，可计算再制造系统成本效益指数的最大值和最小值，求得企业再制造成本效益指数的变化范围，并将产品再制造成本效益指数与之对比，用以对再制造产品的决策。

3 案例

对于某发动机再制造企业，再制造产品产量一定的情况下，选择合适的发动机再制造以获得最大利益，是企业再制造的前提。因此，需要采用再制造成本效益定量分析模型，为企业筛选最具再制造价值的产品。下面以汽车发动机和货车发动机再制造为例，详细阐述其成本效益指数的计算，验证模型的可行性。

3.1 采用德尔菲法确定各因素间相互作用

该企业再制造成本效益主要影响因素为采购因素(PR)、加工因素(PS)、材料利用(MU)以及市场因素(MA)。根据德尔菲法专家评判法，制定专家评分表确定各主因素间的相互影响，专家对各影响因素进行评分。

然后根据专家优化集成搜索模型，得到专家的意见值和可靠度，如表1所示。

表1 专家意见值和可靠度

通过模型求解，综合协调各个专家的意见，得到再制造成本效益指数各个影响因素之间的作用值(矩阵非对角线元素的值)，则再制造成本效益影响因素矩阵为：

同理，分别求出各个因素子因素间的相互作用值，如图4～图7所示。

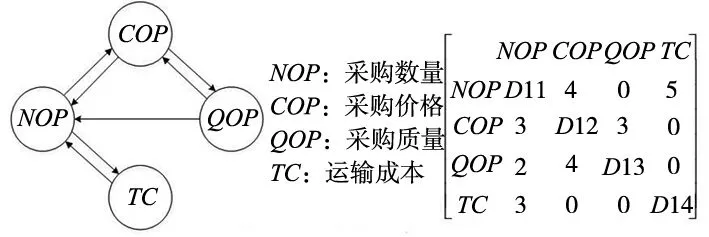
图4 采购因素的子因素有向图和矩阵

图5 加工因素的子因素有向图和矩阵

图6 材料因素的子因素有向图和矩阵

图7 市场因素的子因素有向图和矩阵

3.2 采用熵权法计算各个因素对再制造成本效益的影响值

对于同一企业而言，通过专业评分确定各个因素间的相互影响不会随产品的变化而变化。因此，在选择产品再制造时，只需计算各个产品影响因素对再制造成本效益的影响。再制造成本效益影响因素矩阵对角线的值与各个主因素的子因素有关，不能根据熵权法直接计算，应分别计算产品采购因素、加工因素、材料因素和市场因素各子因素的综合影响值。

针对汽车发动机，其各子因素间对再制造成本效益影响值的计算步骤如下：

(1) 采用专家评价法，对汽车发动机各子因素进行评分。

(2) 对专家的评分值标准化处理。

(3) 计算各专家评分的信息熵和权重。

(4) 对各个指标进行评分，根据式(6)计算最终得分如表2所示。

表2 汽车发动机各子因素对再制造成本效益的影响值

同理，可求得货车发动机各子因素对再制造成本效益的影响值如表3所示。

表3 货车发动机各子因素对再制造成本效益的影响值

3.3 计算再制造成本效益指数

(1) 计算再制造系统成本效益指数的最大值和最小值。确定再制造系统成本效益指数的范围，用以对产品再制造的决策。

根据因素对系统的作用强度表(表2)可知，当各子因素取最大值10时，其对再制造系统成本效益主因素的综合作用强度最大；当各个子因素取最小值1时，其对再制造系统成本效益的作用强度主因素的综合作用强度最小。根据各子因素有向图矩阵(图4～图7)，采用熵权法分别求得各子因素取最大值和最小值时的权重如表4所示。

表4 各子因素分别取最大值和最小值时的权重

由式(7)计算得再制造成本效益各子因素对主因素综合影响的最大值和最小值如表5所示。

表5 各因素对再制造系统影响最大值和最小值

(2) 计算整个系统的成本效益指数(C)范围。当主因素(矩阵对角线元素)取最大值时，得到矩阵：

根据熵权法计算得到各主因素权重如表6所示。

表6 各主因素取最大值和最小值时的权重

根据式(7)，可得各因素对再制造系统成本效益综合影响的最大值，即再制造成本效益指数最大值为：

(8)

同理，计算出再制造系统成本效益指数最小值为：

Cmin=2.17×102

因此，可得到该企业再制造系统成本效益指数的变化范围：2.17×102～2.13×103。

针对汽车发动机，根据汽车发动机各子因素对再制造成本效益的影响值(表2)可确定各子因素有向图的连接矩阵，如下：

汽车发动机采购因素子因素连接矩阵：

汽车发动机加工因素子因素连接矩阵：

汽车发动机材料因素子因素连接矩阵：

根据熵权法计算矩阵中各子因素的权重，结果如表7所示。

表7 汽车发动机各子因素权重

由式(7)求得各子因素对主因素的综合影响值后，可得再制造成本效益影响因素矩阵为：

由熵权法求得各因素的权重，带入式(7)中可得汽车发动机成本效益各影响因素的综合作用值，即汽车发动机再制造成本效益指数CQ：

(9)

同理，根据货车各子因素取值(表3)，求得货车发动机再制造成本效益指数CH：

(10)

经比较可知：Cmin

4 结论

本文建立了再制造工艺全过程的成本效益影响因素指标体系，采用图论方法分析了各主要影响因素之间的相互作用关系，提出了一种联合德尔菲专家评分法和熵权法的定量分析模型，该模型一方面引进专家意见值可靠性指数使评价更加趋于合理，另一方面能有效地计算出不同产品的再制造成本效益指数并进行定量比较。但是，该模型也存在一定的局限，当增加其他再制造成本效益影响因素时会使分析与计算过程更加复杂，从而影响实际结果。随着再制造成本效益研究的不断发展，将会逐渐弥补上述的不足。