数控机床电主轴热误差建模算法研究*

陈光平，肖铁忠

(四川工程职业技术学院 四川省装备制造业机器人应用技术工程实验室，四川 德阳 618000)

0 引言

电主轴是数控成形磨齿机的重要功能性部件。在长时间高速运转过程中，其内部轴承、主轴、转子等零部件会由于摩擦、功率损耗而产生大量的热。虽然一部分热会散发到空气中，一部分会被循环冷却液带走，但仍有相当一部分热量会传递给电主轴本身，使其各部分的温升不均匀、出现温度场并产生相应的热变形，从而对电主轴乃至整个机床的形态精度和加工精度造成显著影响。研究表明，高速数控机床的热变形是影响机床加工精度的重要因素，最高可占机床总体误差的70%[1]。

与成形磨齿过程中机床所受到日照辐射、环境温度、切削热、摩擦热等多种热源相比，电主轴是整个机床最大的热误差源，也是影响齿面加工精度的关键因素之一[2]。为了探明电主轴的热变形机理、减小其热误差，国内外学者进行了大量的研究工作并建立了多种热误差理论模型[3-4]。雷春丽等提出了一种综合了自回归分析理论和灰色系统预测理论的电主轴热误差预测模型，通过采用模糊逻辑选取权值，使各单项预测模型能够扬长避短从而增强组合预测模型的泛化能力[6]。Wang等运用时序分析方法建立了电主轴热误差模型并通过热误差补偿实验检验了模型的精度，取得了较好的效果[6]。Creighton等利用有限元方法分析了微型电主轴系统温度场分布特性并建立了轴向热误差关于转速以及运转时间的指数模型[7]。Raksiri等提出了基于神经网络理论的电主轴温度—热误差建模方法，并依据该模型对电主轴热误差进行预测和在线补偿，从而取得了较好的加工效果[8]。Wang等将数据挖掘理论运用于电主轴的温度—热误差建模方法之中，既增强了热误差模型对于不同工况条件的适应性又进一步提高了电主轴热误差补偿效率[9]。代贵松等通过对电主轴结构及温度场的分析，提出了一种基于自然指数的数控机床电主轴热误差建模方法，具有很好的鲁棒性和很高的准确性[10]。

目前，多元线性回归法是应用较广泛的多变量自回归建模方法之一，具有运算量小、算法简单、模型直观、易于理解、便于实现等诸多优点，在电主轴热误差建模方面得到了广泛应用。但其模型精度往往相对较低，不太适用于成形磨齿机等精密、高精密的数控加工设备。因此，为了探明工况条件下的电主轴温度变化规律，进一步提升电主轴热误差建模精度和机床加工精度，以某成形磨齿机的电主轴为研究对象，通过进行基于工况条件的热误差实验从而获得电主轴主要部位的温升与其轴向、径向的热变形状况。在实验的基础上，提出了由多元二次回归理论—最小二乘法原理建立电主轴径向与轴向热误差预测模型的建模方法，从而对电主轴热误差进行精确性较高地预测。

1 多元二次回归建模方法

假设因变量y与m个自变量x1,x2,…,xm存在非线性关系，依据多元二次回归理论，由实验检测到的n组样本数据(xt1,xt2,…,xtm；yt)，t为时间序列号，t=1,2,…,n，那么这些数据存在如下数学关系：

(1)

则因变量y与自变量x的多元二次回归模型可表示为：

y=α·x+β·x2+ε

(2)

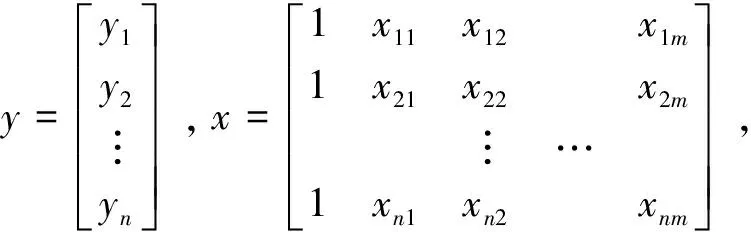
其中，α0,α1,…,αm,β1,β2,…,βm为2m+1个待估计的回归参数；x1,x2,…,xm为m个检测到的样本变量；ε1,ε2,…,εn为n个相互独立并且服从于同一个正态分布N(0,σ)的随机变量。

依据最小二乘法基本原理，为得到估计参数α和β，可假设a0,a1,…,am,b1,b2,…,bm分别为α0,α1,…,αm,β1,β2,…,βm的最小二乘估计参数，则方程组(2)可转化为：

(3)

对于估计参数a和b，需使y的残差平方和达到最小值，即

(4)

若其在最小值处的偏导数为零，那么

(5)

由方程组(5)即可解得估计参数a和b，并将其代入方程(3)，即可得到因变量y与自变量x的、基于最小二乘估计的多元二次回归模型方程。

2 电主轴热误差实验

以某数控成形磨齿机的电主轴为研究对象，其内部包含前、中、后三组滚珠轴承。在长时间高速运转过程中，这三处位置的温升较为明显，也是电主轴的主要热源，故在这些轴承的主轴壳体外表面处安装三个温度传感器，记为Ti(i=1,2,3)。另外，在成形磨齿过程中，砂轮与工件沿机床坐标系Z方向的相对位置误差Δz仅仅影响齿面在齿轮圆周上的位置分布，而对工件齿面本身不会造成任何误差[11]。由于会对齿面加工精度产生显著影响的主要是电主轴分别沿机床坐标系X、Y方向的径向、轴向位置误差，故分别在电主轴的径向与轴向位置安装激光位移传感器，分别记为S1和S2，并将检测到的热变形量分别记为Δx和Δy。电主轴热误差检测过程中的温度、热变形测量点位置如图1所示，热误差实验如图2所示。

图1 电主轴温度与热变形测量点示意图

图2 电主轴热误差实验

温度检测系统采用的是自带热电阻(PT100)传感器的MIK5010A数据记录仪，经过标定的热电阻传感器的温度检测精度为±0.01℃；热变形检测系统采用LTS-25-02型激光位移传感器，其标定后的检测精度为0.01μm。实验期间，车间的环境温度为20±0.2℃，电主轴的工作转速为2500r/min。通过每2min采集一次温度、位移数据，从而得到了电主轴温升变化曲线以及其径向、轴向热误差随时间t的变化曲线，分别如图3和图4所示。

图3 电主轴温升变化曲线图

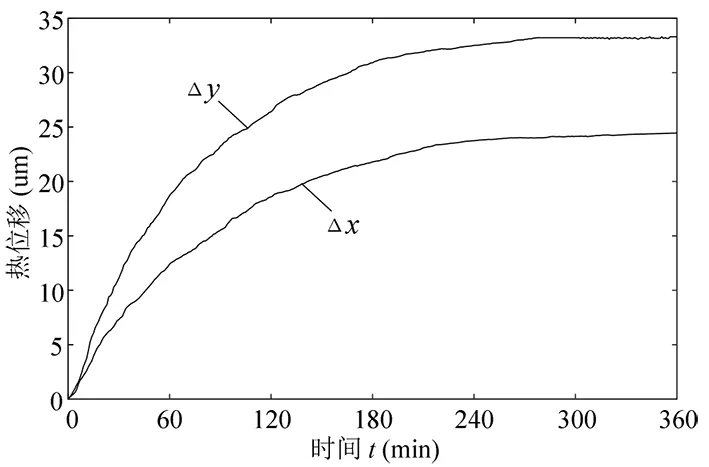
图4 电主轴的径向和轴向热误差变化曲线图

由图3可以看出：在前3个小时内，电主轴的径向、轴向热误差曲线随着运行时间t的增加而快速增长；然后在第3至第4个小时内，热误差曲线的增长速度出现了逐渐变缓的趋势，表明电主轴越来越接近热平衡状态；在第4个小时以后，热误差曲线趋近于直线、基本不再增长，从而表明电主轴已经达到了热平衡状态，其热变形量基本稳定。此外，还可以看出，工况条件下的电主轴径向、轴向热误差曲线的变化趋势与温升密切相关，温升越快，其热变形速度也越快。同时，电主轴热误差曲线无突变、断崖等现象且连续性较好，说明其产品设计与结构性能较好，有利于建立精度高、稳定性强的热误差模型。

3 电主轴热误差模型的建立与应用

运用多元二次回归理论与最小二乘估计原理，将实验检测到的电主轴温度值T1、T2、T3与热变形数据Δx、Δy代入式(5)，解得估计参数a和b并将其代入式(3)，即可得到关于电主轴径向热误差Δx与温度变量T的多元二次回归模型方程为：

Δx=-336.833+9.774T1+3.009T2+

(6)

同理，电主轴轴向热误差Δy与温度变量T的多元二次回归模型方程为：

Δy=-231.644-13.007T1+2.137T2+

(7)

依据式(6)和式(7)，即可得到电主轴径向和轴向热误差的预测曲线Δx′、Δy′以及模型预测值与实验测量值之间的误差曲线εx、εy，如图5所示。由图中可知，当电主轴达到热平衡状态后，由回归模型计算得到的径向、轴向热误差分别为33.808、25.307μm，与实验测量值的最大相对误差分别为1.56%和1.83%，两者均小于1.9%，说明电主轴径向、轴向热误差回归方程的性能可靠、拟合精度高。同时也说明多元二次回归理论对电主轴热误差建模的适用性好，所建立的回归模型具有较好的预测精度。

图5 电主轴径向、轴向热误差预测曲线及拟合误差曲线图

4 结论

电主轴零部件众多、内外部环境热源众多且复杂。以某成形磨齿机的电主轴为研究对象，通过进行热误差实验以获得电主轴温升与其径向、轴向的热变形状况。在实验的基础上，提出了基于多元二次回归理论与最小二乘法原理的电主轴径向与轴向热误差预测模型的建模方法。该方法可以有效解决电主轴热误差建模过程中所遇到的非线性问题并对电主轴热误差进行高精确性地预测。结果表明，回归模型计算值与实验测量值的最大相对误差均小于1.9%。在探明电主轴热误差的变化规律的同时，也为促进数控成形磨齿机加工精度的进一步提升奠定了基础。