发射潜空导弹对潜艇生存概率影响*

张天赫，彭绍雄，王 栋

（海军航空大学，山东 烟台 264001）

0 引言

随着反潜技术的迅速发展，反潜直升机、反潜巡逻机等航空反潜平台装备部队，由于缺乏有效的对空硬打击能力，在潜空对抗的过程中，一旦潜艇被发现，潜艇的生存概率在30%以下，而反潜机的生存概率却接近100%［1］，使得防空能力成为提高潜艇安全和生存的关键。潜空导弹对潜艇生存概率的影响因素多、条件复杂且相互关联，因此，分析潜空导弹武器系统的作战效能，为潜艇防空武器系统的设计、改进以及潜空作战提供理论依据，对于加强潜艇对敌反潜机的防御能力，提高潜艇的生存概率具有重要意义。

1 双方作战状态

1.1 潜艇初始状态

潜艇在执行任务的过程中，根据其在水上水下的状态可将潜艇航行分为水面航行、半潜航行、潜望深度航行及工作深度航行［2］，如图1所示。

1.1.1 水面航行状态

潜艇漂浮于海面之上，并可潜入海底的航行状态。

1.1.2 半潜航行状态

潜艇主体结构在海面之下，少量上层结构露出海面，并可潜入海底或浮出海面。这是潜艇在水面航行状态与潜望深度航行状态中的一种中间状态。

1.1.3 潜望深度航行状态

潜艇可在水下使用潜望镜观察的航行状态。

1.1.4 工作深度航行状态

潜艇处于安全深度（防止与舰艇和冰层碰撞的深度）以下和90%极限深度以上的海中进行航行的状态（该深度通常无法发射潜空导弹，本文不作详细研究）。

1.2 反潜机反潜方式

1.2.1 反潜直升机反潜方式

全向螺旋形搜索是指反潜直升机在应召搜索条件下，已知目标最后丢失点的位置而采取的搜潜方式。

扇面搜索法通常是指反潜直升机在丢失目标信息后，找到了潜艇最后丢失点及潜艇的概略航向时所采用搜潜方式。

反潜直升机全向螺旋形搜索示意图与扇面搜索示意图如图2和图3所示。

1.2.2 反潜巡逻机反潜方式

圆形搜索法，是指对于已知初始目标位置点的情况，为缩短搜潜时间，尽快覆盖较大海域时所采取的搜潜方式。

拦截线形搜索法，是指对于己知潜艇初始位置点及概略航向时，在潜艇运动方向前所布置的线型声纳浮标拦截阵的搜潜方式。

反潜巡逻机圆形搜索示意图与拦截线型搜索示意图如图4和图5所示。

2 潜艇生存概率模型

2.1 确定评价指标

研究潜艇发射潜空导弹对潜艇生存概率影响的组成指标较多，条件较为复杂。为了优化评价指标体系［3］，最大程度地反映发射潜空导弹对潜艇生存概率的影响。本文从潜艇初始状态，潜空导弹战备完好性，射前准备能力，武控系统能力，导弹攻击目标能力，敌机种类及搜潜方式6个方面对潜艇的生存概率的指标体系进行分析，指标体系如下页图6所示。

2.2 贝叶斯网络介绍

贝叶斯网络是在20世纪80年代由Pearl提出来的，它是为了解决不定性和不完整的问题提出的，它是一个有向无圈图，每个节点代表随机变量，节点间的边代表变量之间关系，每个节点都附有一个概率分布，其中条件概率表示关系大小，无上层节点的用先验概率表达。一个有N个节点的贝叶斯网络可以用 N=〈〈V，E〉，P〉来表示，其中，〈V，E〉表示一个有向无圈图 G，节点 V=｛V1，V2，…，Vn｝代表随机变量，有相边E表示节点之间的相互联系；P代表概率分布。

针对有向边（Vi，Vj），Vi为Vj的父节点，反之Vj为Vi的子节点。没有父节点的节点用先验概率表示。设Pa（Vi）为Vi的父节点集合，A（Vi）为非子节点集合，在贝叶斯网络中满足下式：

P（Vi|Pa（Vi），A（Vi））=P（Vi|Pa（Vi））在给定条件概率和先验概率的情况下，可得所有节点的联合概率分布：

分析构建的指标体系及潜艇生存概率的影响因素可以发现：1）战备能力（Combat Readiness，CR）通过影响评价体系中的潜艇初始状态（U1）、战备完好性（U2）、射前准备能力（U3）3 个一级指标来影响潜空导弹作战效能。2）U2及U3通过影响平台性能（Platform Permance，PP）来影响潜空导弹作战效能。3）指标U4和U5属于导弹性能（Missile Performance，MP）的范围，导弹性能必然也是影响潜空导弹作战性能的重要指标之一。4）指标U6为反潜机的机种及反潜方式，对潜艇生存概率产生直接影响。5）潜艇的生存概率P=A+0.3×（1-A）。为此，根据各指标对潜空导弹作战效能的网络关系，可构建如图7所示的潜空导弹的贝叶斯网络模型［6］。

结合构建的贝叶斯网络以及条件概率和先验概率公式，得到潜空导弹命中率A的联合概率PA为：

2.3 贝叶斯网络建模

由贝叶斯网络理论可知，求解贝叶斯网络解最主要是要构建贝叶斯网络结构，计算各节点的条件概率或先验概率。结合潜艇生存概率的评价指标，易发现，在构建的贝叶斯网络中，根节点CR、U4、U5及U6有独立评价指标，因此，本文先采用模糊综合评价法确定CR、U4、U5及U6的先验概率。然后利用专家打分法确定各节点的条件概率分布表（CPT），并利用软件仿真贝叶斯网络模型，介绍求解流程。

2.3.1 确定先验概率

模糊综合评价法是一种基于模糊数学的综合评价方法，可利用隶属度理论将定性问题转化为定量问题。由李德毅院士提出的云模型理论［12］把模糊性和随机性完全结合到一起，构成了定性与定量间的相互映射。通常，云模型的数字特征可用（Ex，En，He）表示，其中，Ex是期望值，是定性概念的基本确定性的度量，是在论域中云滴分布的数学期望；En是熵，是定性概念不确定性的度量，反映了云滴的离散程度，He是超熵，是熵的熵，也就是熵的不确定度量。云模型的隶属度可通过下列步骤计算获得：

1）生成以En为期望值，方差为He2的正态随机数，记为 En'；

2）生成以Ex为期望值，方差为En的正态随机数，记为x；

3）计算隶属度，即

式中，Ex为各评语的期望值；En'的取值遵循“3b规则”，可得En'为相邻两个期望值差的1/3。

计算云模型隶属度，然后计算根节点CR、U4、U5及U6的先验概率，其计算方法［7］如下所示：

1）确定评价指标集U=｛U1，U2，…，Um｝，Uj（j=1，2，…，m），代表各种影响评价的指标。

2）确定评价集V=｛V1，V2，…，Vs｝，并确定决策值C=｛c1，c2，…，cs｝，其中，s为评语的数量，Vj（j=1，2，…，s）为各等级所对应的评语。

3）确定权重向量 W=｛w1，w2，…，wm｝。首先评价指标进行去量纲，得D=（dij）m×n

则第i个评价指标的熵为：

式中：

则可获得第i个评价指标的权重为

4）构造隶属度权重矩阵R

邀请p位相关领域专家对构建的m个指标进行打分，获得矩阵X=（xij）p×m，xij代表第i名专家对第j个指标打分。令δjd表示第j个指标隶属于第d个评判等级的隶属度，可得δjd的表达式

可得隶属度权重rid为

其中，d=1，2，…，s，隶属度权重矩阵 R 为

5）确定根节点先验概率。由获得的指标权重，得到评价向量B为：

B=W·R=（b1，b2，…，bn）

式中，bj（j=1，2，…，s）表示评价结果隶属于评判集j的隶属度，也就是先验概率。

2.3.2 基于专家经验法的CPT确定

贝叶斯网络中的条件概率的确定，可由专家根据经验直接给出，为说明问题，以节点A与节点U6为例可获得条件概率分布表（CPT）如表1所示。表中，同一列的概率总和为100%。同理，可获得其他节点的条件概率分布表（CPT）。

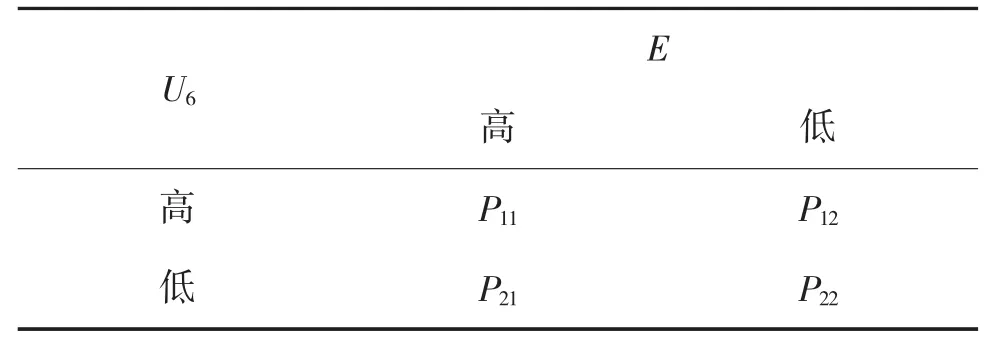
表1 节点E与节点U6的CPT

3 算例仿真与计算

为了验证构建评价模型的准确性与可靠性，现使用该模型对某型潜空导弹的作战效能进行评估。现给出如图8所示的评价流程，下面进行具体介绍评价流程。

3.1 邀请专家确定指标

为使模型可靠性较高，邀请相关专业的5位专家对某潜空导弹作战性能进行相关评价，首先将各指标的评价等级分为高低2个等级，由专家经验法，设定各指标等级的数值区间，得到如表2所示指标等级及区间数值表。

表2 指标等级及区间数值表

3.2 获取数据

该数据是指贝叶斯网络模型中与根节点相对应的子指标数据。即CR、U4、U5及U64个根节点的数据，其中各根节点且均有指标评价体系，如U4包含 V41、V42、V43及 V444 个子指标。

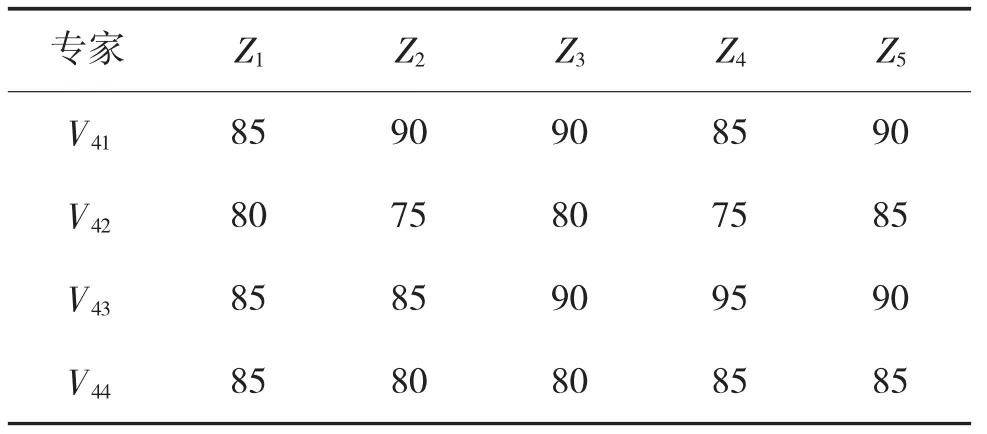
表3 子指标V41～V44专家打分

3.3 指标去量纲处理

由于构建的评价指标体系中，同时有定量指标与定性指标，且各指标的单位互不相同，为统一量纲，需对所有的数据进行去量纲，对于定性指标，由于各指标的打分使用百分制。因此，可直接将分数除100。为说明情况，以对子指标V41～V44进行去量纲为例，如表4所示。

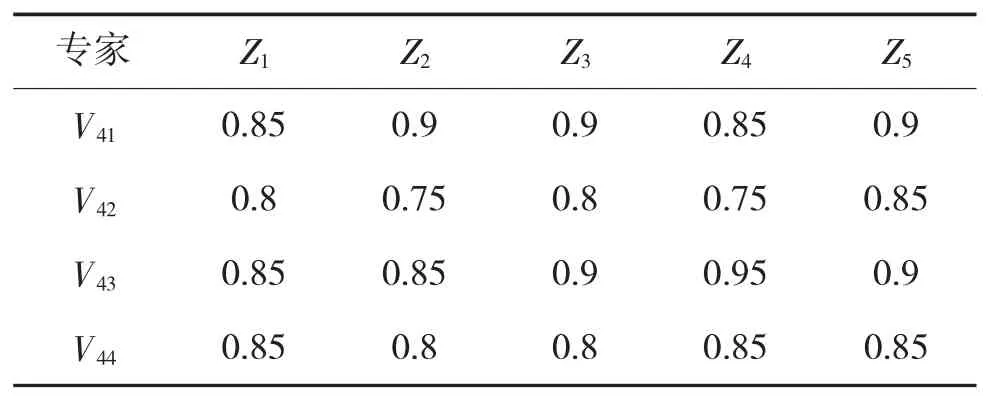
表4 子指标V41～V44无量纲指标值

3.4 确定根节点先验概率

由于网络节点较为复杂，为举例说明情况，以根节点U4为例说明确定流程。

1）确定评价因素集 U=｛B41，B42，B43，B44｝；

2）确定评价集V=｛高，低｝和决策值集C=｛80，40｝；

3）利用熵权法求指标权重，得到去量纲矩阵D=（dij）m×n。

指标的熵为 H=｛0.9997，0.9993，0.9994，0.9997｝，指标 V41～V44的权重向量 W=｛0.1378，0.3955，0.3118，0.154 9｝，而与评价集相对应云模型的数学期望值为 Exd=｛80，40｝，熵为 En'=40/3，评价集的隶属云如图9所示。

4）构造隶属度权重矩阵

根据表3中所给出的子指标V41～V44的打分，计算得出指标V41～V44的隶属度权重矩阵R为

5）根据所求的隶属度权重矩阵，可得U4的先验概率为 P（U4）=｛0.995，0.005｝，同理可得 CR 的P（CR）=｛0.996 4，0.003 6｝，P（U5）=｛0.993，0.007｝，P（U6）=｛0.413，0.587｝。

3.5 确定条件概率表（CPT）

根据指标体系，及指标对潜艇生存概率的影响情况，由相关领域专家确定各节点的条件概率表（CPT）。由于贝叶斯网络节点多而复杂，现以节点U6与节点E为例，构建的条件概率表如表5所示。

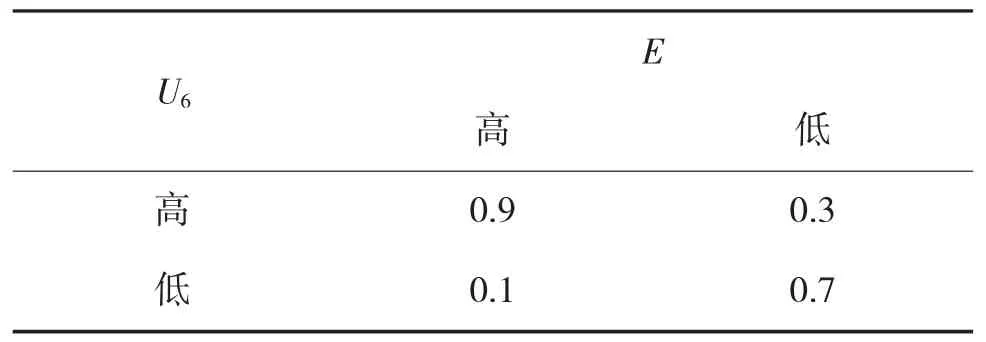
表5 节点U6与节点E的CPT

3.6 模型仿真

Netica是一款专门求解贝叶斯网络问题的图形化软件。在解决贝叶斯网络问题方面功能强大，画面直观。为了对建立的贝叶斯模型进行仿真，确定模型的有效性和可靠性，现利用Netica软件进行仿真，Netica仿真图如图10所示。

从图中可以直接得出导弹命中概率隶属于评价集的概率为：高的概率为0.76，低的概率为0.24。综合分析评价结果，本次潜艇的生存概率为0.832，生存概率较高。

3.7 模型有效性分析

模型的有效性分析是检验模型正确性的重要方法。下面对模型的有效性进行分析，本文拟在3种特殊条件下的模型进行了仿真，仿真结果如下页表6所示。

分析表 6 可知，保证指标 U4、U5、U6不变，设定战备能力CR为低时，则潜艇的生存概率为0.56；保持战备能力 CR、U6不变，当 U4、U5同时低时，则潜艇的生存概率为0.773；当保证CR、U4、U5不变时，U6低时，则潜艇的生存概率为0.74。进一步分析，从先验概率变化到评价结果的概率变化可以看出CR、U6是影响潜空导弹发射过程中的关键因素，当战备能力低时，潜空导弹的命中率一定会很低，而反潜机的种类与反潜方式对潜空导弹的命中率也有较大影响。这个结论与潜艇部队实际发射潜空导弹时的影响因素相一致，也从侧面验证了该模型的有效性［4-20］。

表6 节点敏感度仿真结果

4 结论

潜艇在水下面对复杂多变的战场环境，尤其受到来自空中目标的威胁，对空中目标的打击能力已成为潜艇必备能力。本文基于这个考虑研究了基于贝叶斯网络的潜空导弹对潜生存概率的影响。